Ada tiga metode penarikan kesimpulan yang sah dalam bahasan logika matematika yaitu modus ponens, modus tollens, dan silogisme. Penarikan kesimpulan dalam logika matematika sama dengan mendapatkan argumen yang tidak bertentangan dengan premis-premis. Kesimpulan yang sah didapatkan melalui metode penarikan kesimpulan dalam logika matematika.
Kesimpulan merupakan hasil akhir dari sebuah pemikiran. Kesimpulan juga dapat dikatakan sebagai sebuah gagasan yang tercapai pada akhir pembicaraan. Pada bahasan logika matematika, kesimpulan adalah suatu proposisi dari beberapa premis atau argumen/ide pemikiran dengan aturan-aturan yang telah ditetapkan.
Diketahui ada 3 metode penarikan kesimpulan dalam logika matematika. Bagaimana perbedaan dari setiap metode penarikan kesimpulan yang sah tersebut? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Modus Ponens
Penarikan kesimpulan modus ponens mengikuti aturan kesimpulan yang sah untuk jika p maka q dan p maka q harus benar. Premis pertama pada modus ponens berupa implikasi, yaitu jika p maka q sedangkan premis kedua berupa proposisi tunggal, yaitu p. Kesimpulan yang sah dari argumen tersebut berupa proposisi tunggal, yaitu q.
Sebagai contoh diketahui dua premis Jika hari ini langit mendung maka hari ini akan hujan dan Hari ini akan hujan.
Premis pertama terdiri atas dua proposisi tunggal yaitu p = hari ini langit mendung dan q = hari ini akan hujan dengan operator logika implikasi.
Sementara premis kedua berupa sebuah proposisi tunggal, yaitu hari ini akan hujan. Kesimpulan yang sah dari argumen tersebut menurut metode penarikan kesimpulan modus ponens adalah hari ini akan hujan.

Kesimpulan yang sah pada modus ponens ini dapat dibuktikan melalui tabel kebenaran. Hasil akhir nilai kebenaran dari kesimpulan pada modus ponens berupa tautologi. Nilai kebenaran berbentuk tautologi pada kolom (p ⇒ q ∧ p) ⇒ q dapat menjadi bukti bahwa modus ponens merupakan kesimpulan yang sah/berlaku.
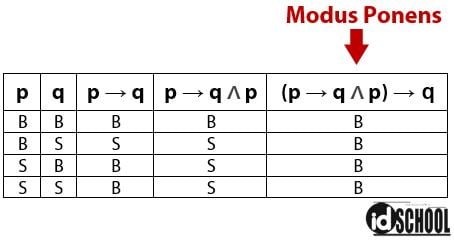
Baca Juga: Pengertian Tautologi, Kontradiksi, dan Kontingensi
Modus Tollens
Penarikan kesimpulan modus tollens mengikuti aturan kesimpulan yang sah untuk jika p maka q dan ~q maka ~p harus benar. Diasumsikan jika p maka q (p ⇒ q) bernilai benar dan diketahui ingkaran q (~q) bernilai benar. Sehingga, agar implikasi dari p dan q bernilai benar maka ingkaran p (~p) harus benar.
Sebagai contoh: diketahui dua premis jika hari ini langit mendung maka hari ini akan hujan dan hari ini tidak akan hujan.
Premis pertama terdiri atas dua proposisi tunggal yaitu p = hari ini langit mendung dan q = hari ini akan hujan. Premis kedua berupa sebuah proposisi tunggal bernilai benar, yaitu hari ini tidak akan hujan.
Kesimpulan yang sah dari argumen tersebut menurut dengan metode penarikan kesimpulan modus tollens adalah Hari ini langit tidak mendung.

Bukti dari kesimpulan yang sah untuk modus tollens dapat dibuktikan melalui tabel kebenaran. Semua nilai kebenaran Benar (B) atau tautologi pada kolom (p → q ∧ ~q) → ~p menunjukkan bukti penarikan kesimpulan yang sah. Perhatikan tabel kebenaran untuk ekspresi logika (p → q ∧ ~q) → ~p berikut menghasilkan tautologi.

Baca Juga: Logika Matematika (Konjungsi, Disjungsi, Implikasi, dan Biimplikasi)
Silogisme
Kesimpulan yang sah dari metode silogisme merupakan kesimpulan dari keadaan yang umum ke yang khusus. Aturan dasar penarikan kesimpulan silogisme menyatakan bahwa jika p maka q dan jika q maka r keduanya bernilai benar menghasilkan kesimpulan jika p maka r juga bernilai benar.
Dengan kata lain, hasil penarikan kesimpulan silogisme digunakan ketika konsekuen premis pertama sama dengan anteseden premis kedua. Hasil penarikan kesimpulan silogisme adalah implikasi dari anteseden premis pertama dan konsekuen premis kedua.
Sebagai contoh diketahui dua premis: Jika hari ini langit mendung maka hari ini akan hujan dan Jika hari ini akan hujan maka Doni akan membawa payung.
Premis pertama terdiri atas dua proposisi tunggal, yaitu p = Hari ini langit mendung dan q = hari ini akan hujan. Premis kedua juga terdiri dari dua sebuah proposisi tunggal, yaitu q = Hari ini akan hujan dan r = Doni membawa payung.
Kesimpulan yang sah dari argumen tersebut menurut metode penarikan kesimpulan silogisme adalah Jika hari ini langit mendung maka Doni membawa payung.

Bukti dari kesimpulan yang sah untuk silogisme juga dapat dibuktikan melalui tabel kebenaran. Bukti yang benar akan menunjukkan bentuk tautologi pada kolom [(p → q) ∧ (q → r)] → (p→r) seperti yang ditunjukkan pada tabel kebenaran berikut.
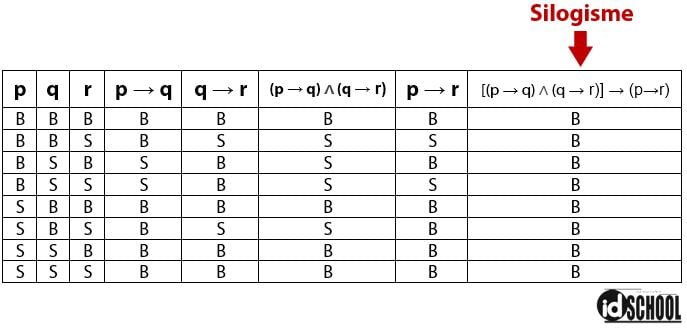
Baca Juga: Cara Melengkapi Tabel Kebenaran
Contoh Soal Penarikan Kesimpulan yang Sah
Soal dapat menjadi tolak ukur pemahaman akan suatu materi. Mengerjakan soal mampu menambah pemahaman akan suatu materi. Beberapa soal berikut akan melatih kemampuan sobat idschool dalam memahami materi penarikan kesimpulan.
Contoh 1 – Soal Penarikan Kesimpulan
Diketahui premis-premis sebagai berikut.
- Jika Siti sakit maka dia pergi ke dokter
- Jika Siti pergi ke dokter maka dia diberi obat
Penarikan kesimpulan yang sah dari argumentasi di atas adalah ….
A. Jika Siti sakit maka Siti pergi ke dokter dan diberi obat
B. Jika Siti sakit dan dia pergi ke dokter maka Siti diberi obat
C. Jika Siti sakit maka Siti diberi obat
D. Siti sakit dan pergi ke dokter dan diberi obat
E. Siti sakit dan pergi ke dokter atau diberi obat
Pembahasan:
Misalkan proposisi pada premis-premis disimbolkan dengan huruf-huruf p, q, dan r seperti berikut.
- p = Siti sakit
- q = Siti pergi ke dokter
- r = Siti diberi obat
Sehingga, premis-premis dapat dinyatakan dalam simbol seperti berikut.
- Premis 1: Jika Siti sakit maka dia pergi ke dokter (p ⇒ q)
- Premis 2: Jika Siti pergi ke dokter maka dia diberi obat (q ⇒ r)
Penarikan kesimpulan dari arugumen pada soal dapat menggunakan penarikan kesimpula sillogisme karena konsekuen pada premis 1 sama dengan anteseden pada premis 2. Diperoleh hasil penarikan kesimpulan yang sah seperti berikut
Premis 1: p ⇒ q
Premis 2: q ⇒ r
—————-
∴ p ⇒ r
Diketahui bahwa p = Siti sakit dan q = Siti diberi obat, sehingga p ⇒ r adalah Jika Siti sakit maka Siti diberi obat. Jadi, kesimpulan yang sah dari argumentasi pada soal adalah Jika Siti sakit maka Siti diberi obat.
Jawaban: C
Contoh 2 – Soal Penarikan Kesimpulan yang Sah
Ditentukan premis-premis sebagai berikut:
- Jika Biden makan emping maka penyakitnya kambuh.
- Jika penyakitnya kambuh maka Biden pergi ke dokter.
Negasi dari penarikan kesimpulan yang sah dari kedua pressmis tersebut adalah ….
A. Jika Biden makan emping maka ia pergi ke dokter.
B. Jika Biden tidak makan emping maka ia pergi k e dokter
C. Jika Biden tidak makan emping maka ia tidak pergi ke dokter
D. Biden makan emping dan ia tidak pergi ke dokter
E. Biden tidak makan emping dan ia tidak pergi ke dokter
Pembahasan:
Misalkan proposisi dari premis-premis tersebut disimbolkan dengan huruf p, q, dan r seperti berikut.
- p = Biden makan emping
- q = Biden penyakitnya kambuh
- r = Biden pergi ke dokter
Maka simbol yang sesuai untuk kedua premis akan menjadi seperti bentuk berikut.
- Premis 1: p ⇒ q
- Premis 2: q ⇒ r
Penarikan kesimpulan yang sesuai untuk dua bentuk kedua premis di atas adalah silogisme seperti cara penyelesaian berikut.
Premis 2: q ⇒ r
—————-
∴ p ⇒ r
Diperoleh penarikan kesimpulan yang sah yaitu p ⇒ r sehingga bentuk negasi atau ingkaran dari p ⇒ r adalah ~(p ⇒ r) = p ∧ ~ r. Jadi, kesimpulan yang sah dari argumentasi pada soal adalah Biden makan emping dan ia tidak pergi ke dokter.
Jawaban: C
Contoh 3 – Soal Penarikan Kesimpulan
Ditentukan premis-premis sebagai berikut:
- Jika Jono naik bis maka ia terlambat masuk sekolah.
- Jono tidak terlambat masuk sekolah.
Ingkaran dari kesimpulan yang sah adalah ….
A. Jono tidak naik bis
B. Jono naik bis
C. Jono terlambat masuk sekolah
D. Jono naik bis dan ia tidak terlambat masuk sekolah
E. Jono tidak naik bis dan ia terlambat masuk sekolah
Pembahasan:
Misalkan proposisi dari premis-premis tersebut dengan simbol huruf p dan q seperti berikut.
- p = Jono naik bis
- q = ia terlambat masuk sekolah
Kedua premis yang diberikan pada soal dapat disimbolkan seperti berikut.
- Premis 1: p ⇒ q
- Premis 2: ~q
Untuk bentuk seperti kedua premis di atas menggukan metode penarikan kesimpulan modus tollens seperti penyelesaian berikut.
Premis 1: p ⇒ q
Premis 2: ~q
—————-
∴ ~p
Diperoleh kesimpulan yang sah ~p atau Jono tidak naik bis. Bentuk negari atau ingkaran dari kesimpulan yang sah adalah ~p: ~(~p) = p. Jadi, kesimpulan yang sah dari argumentasi pada soal adalah Jono naik bis.
Jawaban: C
Demikianlah ulasan materi 3 metode penarikan kesimpulan dalam logika matematika yang terdiri dari modus ponens, modus tollens, dan silogisme. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Konvers, Invers, dan Kontraposisi dari Suatu Implikasi
