Bentuk tautologi kontradiksi dan kontingensi dari suatu ekspresi logika matematika secara berturut-turut memiliki karakteristik nilai kebenaran yang selalu benar, selalu salah, dan bisa benar/salah. Cara mengetahui suatu ekspresi logika memiliki bentuk tautologi kontradiksi dan kontingensi dapat ditentukan menggunakan tabel kebenaran dalam logika matematika. Tabel kebenaran adalah tabel yang memuat semua kemungkinan nilai kebenaran dari proposisi majemuk untuk beberapa kombinasi nilai kebenaran.
Sebuah proposisi tunggal hanya dapat memiliki satu nilai kebenaran yaitu salah (S) atau benar (B). Nilai kebenaran dari proposisi majemuk suatu ekspresi logika bergantung pada nilai kebenaran proposisi tunggal dan operator logikanya.
Beberapa ekspresi logika memberikan nilai kebenaran yang selalu benar. Beberapa ekspresi logika lainnya memberikan nilai kebenaran yang selalu salah. Dan beberapa ekspresi logika juga dapat memiliki nilai kebenaran yang dapat bernilai benar dan salah.
Ketiga hasil berbeda yang dapat diperoleh menjadikan ekspresi logika dapat memiliki tiga karakteristik nilai kebenaran yang berbeda. Ketiga karakteristik tersebut merupakan tautologi kontradiksi dan kontingensi. Apa itu Tautologi Kontradiksi dan Kontingensi? Bagaimana perbedaan dari tiga bentuk ekspresi logika yang merupakan Tautologi Kontradiksi dan Kontingensi? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Tautologi
- Kontradiksi
- Kontingensi
- Contoh Soal dan Pembahasan Menentukan Tautologi Kontradiksi dan Kontingensi
Baca Juga: Logika Matematika (Konjungsi, Disjungsi, Implikasi, dan Biimplikasi)
Tautologi
Tautologi adalah ekspresi logika dari pernyataan majemuk yang selalu bernilai benar. Apapun nilai kebenaran proposisi tunggalnya, ekspresi logika yang merupakan tautologi akan selau menghasilkan nilai benar. Proposisi mejemuk yang termasuk dalam tautologi dapat secara mudah dilihat melalui tabel kebenaran yang semuanya bernilai Benar (B).
Sebagai contoh nilai kebenaran dari ekspresi logika (p ∧ q) → (p → q), diperoleh bentuk tautologi seperti yang ditunjukkan pada tabel di bawah.
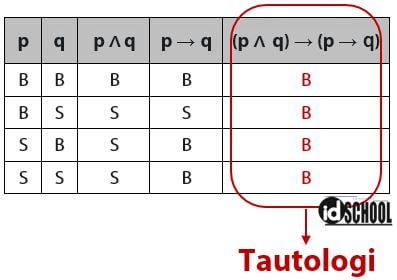
Kontradiksi
Kontradiksi adalah suatu proposisi majemuk dengan nilai kebenaran selalu salah untuk semua kombinasi nilai kebenaran dari proposisi tunggal yang membentuknya. Sehingga dapat dikatakan bahwa kontradiksi merupakan kebalikan dari tautologi. Apapun nilai kebenaran dari proposisi tunggalnya baik benar (B) atau salah (S), nilai kebenaran proposisi majemuk dari suatu ekspresi logika matematika yang merupakan kontradiksi akan salah.
Proposisi majemuk yang termasuk dalam kontradiksi dapat secara mudah dilihat melalui tabel kebenaran. Sebagai contoh, periksa nilai kebenaran dari ekspresi logika (p ∧ q) ↔ (p → ~q)!

Baca Juga: Cara Melengkapi Tabel Kebenaran dalam Logika Matematika
Kontingensi
Berikutnya adalah ekspresi logika yang tidak selalu bernilai benar dan tidak selalu bernilai salah, atau dapat bernilai benar dan dapat bernilai salah bergantung dari nilai kebenara proposisi tunggal dan operator logikanya. Ekspresi logika yang dapat menghasilkan nilai benar atau salah dalam logika matematika disebut kontingensi.
Kontingensi adalah suatu proposisi majemuk dengan nilai kebenaran benar (B) dan salah (S). Nilai kebenaran ini tergantung dari nilai kebenaran proposisi tunggal pembentuknya dan operator logika penghubungnya.
Proposisi majemuk yang termasuk kontingensi dapat dilihat melalui tabel kebenaran. Sebagai contoh ekspresi logika yang termasuk kontingensi: periksa nilai kebenaran dari ekspresi logika (p ∧ q) ↔ p!
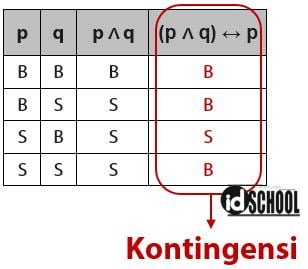
Contoh Soal dan Pembahasan Menentukan Tautologi Kontradiksi dan Kontingensi
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal dan Cara Menentukan Tautologi Kontradiksi dan Kontingensi
Pernyataan berikut yang merupakan tautologi adalah ….
A. q ∧ (p ⇒ q)
B. (p ∧ q) ⇒ ~p
C. ~(p ⇒ q) ⇔ (p ∧ ~q)
D. ~(p ∧ q) ⇔ p
E. ~p ∧ (~p ⇒ ~q)
Pembahasan:
Tautologi terdapat pada ekspresi logika yang selalu menghasilkan nilai kebenaran yang benar. Nilai kebenaran untuk lima ekspresi logika pada pilihan ganda sesuai dengan tabel berikut.
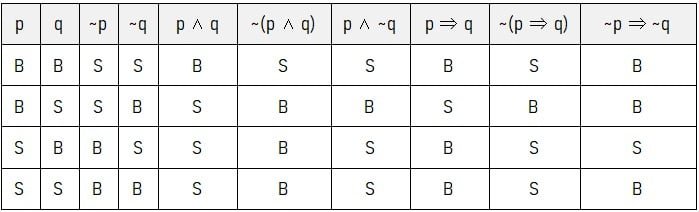
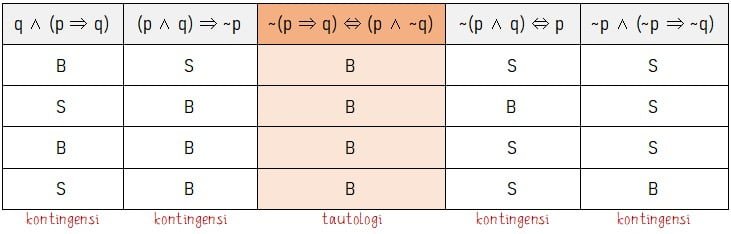
Jadi, pernyataan berikut yang merupakan tautologi adalah ~(p ⇒ q) ⇔ (p ∧ ~q),
Jawaban: C
Baca Juga: Konvers Invers dan Kontraposisi dari Suatu Implikasi
Contoh 2 – Soal dan Cara Menentukan Tautologi Kontradiksi dan Kontingensi
Perhatikan pernyataan berikut!
i. (~p ∨ q) ⇔ (~q ^ p)
ii. (p ∧ q) ⇔ (p ∨ q)
iii. (~p ∧ q) ⇔ ~(p ∨ ~q)
Pernyataan yang termasuk sebagai kontradiksi ditunjukkan oleh nomor ….
A. i saja
B. ii saja
C. i dan ii
D. i dan iii
E. i, ii, dan iii
Pembahasan:
Kontradiksi terdapat pada ekspresi logika yang selalu menghasilkan nilai kebenaran yang salah. Nilai kebenaran untuk lima ekspresi logika pada pilihan ganda sesuai dengan tabel berikut.
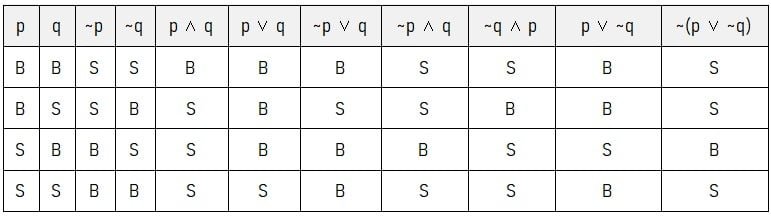

Jadi, pernyataan yang termasuk sebagai kontradiksi ditunjukkan oleh nomor i saja.
Jawaban: A
Sekian ulasan mengenai pengertian dan karakteristik tautologi kontradiksi dan kontingensi dari suatu ekspresi logika matematika. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
