Aturan Cosinus: Materi dan Contoh Soal + Pembahasan

Persamaan pada aturan cosinus menyatakan hubungan antara kuadrat panjang sisi dengan nilai cosinus dari salah satu sudut pada segitiga. Aturan cosinus dapat digunakan untuk menentukan besar salah satu sudut segitiga saat tiga sisi segitiga diketahui. Sedangkan untuk menentukan salah satu sisi segitiga, aturan cosinus dapat digunakan saat diketahui dua sisi dan sudut apitnya.

Selain aturan cosinus, terdapat pula aturan sinus yang dapat digunakan untuk menentukan sisi segitiga atau sudut segitiga yang belum diketahui. Kapan menggunakan aturan sinus? Kapan menggunakan aturan cosinus? Hal ini tergantung apa yang diketahui di soal.

Bahasan mengenai bentuk 3 rumus pada aturan cosinus diberikan seperti ulasan di bawah. Pada bagian akhir ditunjukkan kapan aturan ini digunakan untuk menyelesaikan suatu soal. Sehingga, sobat idschool perlu menyimak bahasan sampai bagian akhir.

Table of Contents

• Pengantar Materi Aturan Cosinus
• Contoh Soal dan Pembahasan
  • Contoh 1 – Mencari Besar Salah Satu Sudut Segitiga
  • Contoh 2 – Aplikasi Rumus

Pengantar Materi Aturan Cosinus

Sudah disinggung sedikit sebelumnya, bahwa aturan cosinus dapat digunakan untuk menentukan panjang salah satu sisi segitiga. Selain itu, aturan cosinus dapat digunakan untuk mengetahui besar salah satu sudut segitiga. Persamaan yang terdapat pada aturan cosinus diperoleh dengan memanfaatkan fungsi trigonometri dan teorema pythagoras.

Dari mana persamaan pada aturan cosinus diperoleh? Cari tahu jawabannya pada ulasan di bawah.

Perhatikan gambar sebuah segitiga di bawah!

Berdasarkan ∆DBC maka dapat diperoleh tiga persamaan seperti berikut.

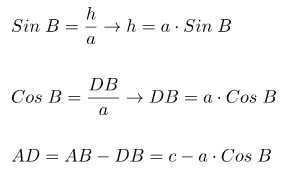
Dari ∆ADC dan teorema pythagoras dapat diperoleh persamaan di bawah.

AC²= AD²+ CD²
b² = ( c – a ⋅ Cos B)² + ( a ⋅ Sin B)²
b² = c² – 2ac ⋅ Cos B + a² ⋅ Cos² B + a² ⋅ Sin²B
b² = c² – 2ac ⋅ Cos B + a² ( Cos²B + Sin²B)
b² = c² – 2ac ⋅ Cos B + a² ⋅ 1
b² = c² – 2ac ⋅ Cos B + a²
b² = c² + a² – 2ac ⋅ Cos B

Persamaan akhir yang di atas merupakan salah satu bentuk rumus pada aturan cosinus.
Dengan mengikuti langkah serupa seperti yang telah dikerjakan di atas, akan diperoleh dua persamaan lainnya. Sehingga, ada tiga persamaan yang terdapat pada aturan cosinus seperti pada ringkasan berikut.

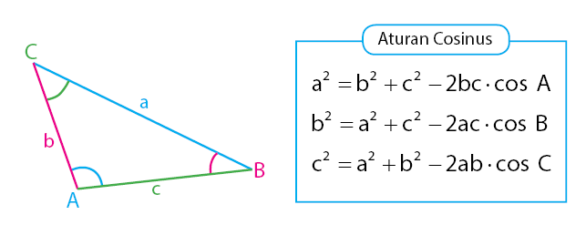
Berdasarkan tiga persamaan aturan cosinus di atas, dapat diperoleh rumus fungsi cosinus yang dapat digunakan untuk menentukan besar sudut segitiga jika diketahui panjang ketiga sisi segitiga. Persamaan fungsi cosinus tersebut dapat dilihat pada persamaan di bawah.

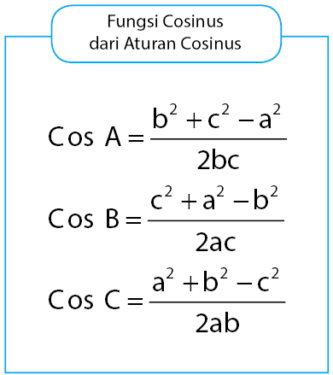
Baca Juga: Identitas Trigonometri Lengkap

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Mencari Besar Salah Satu Sudut Segitiga

Pada suatu segitiga dengan sisi – sisi a, b, dan c memenuhi a² – b² = c² – bc. Maka besar sudut A adalah ….
A. 90^o
B. 60^o
C. 45^o
D. 30^o
E. 15^o

Pembahasan:
Dari soal diberikan informasi bahwa a² – b² = c² – bc, sehingga dapat diperoleh a² = b² + c² – bc.
Rumus cosinus: a² = b² + c² – 2bc ⋅ cos A

Berdasarkan dua persamaan di atas, akan diperoleh nilai cos A.

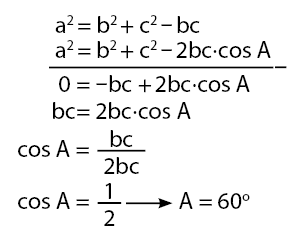
Jadi, besar sudut A adalah 60^o.

Jawaban: B

Contoh 2 – Aplikasi Rumus

Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 40 mil dengan arah 30^o dari A kemudian berputar haluan dilanjutkan ke pelabuhan C sejauh 60 mil dengan arah 150^o dari B. Jarak terdekat dari pelabuhan A dan C adalah ….
A. 20√2 mil
B. 20√3 mil
C. 20√5 mil
D. 20√7 mil
E. 20√11 mil

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat dibuat sebuah ilustrasi gambar seperti berikut.

Menghitung jarak terdekat dari pelabuhan A dan C:

Jadi, Jarak terdekat dari pelabuhan A dan C adalah 20√7 mil.

Jawaban: D

Sekian pembahasan aturan cosinus yang meliputi 3 bentuk rumus dan contoh soal beserta dengan dengan pembahasannya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Fungsi Trigonometri untuk Menghitung Luas Segitiga Sembarang