Biaya produksi minimum atau keuntungan maksimum dari sebuah usaha yang dinyatakan dalam sebuah fungsi dapat dicari melalui turunan pertama fungsi. Permasalahan biaya minimum atau keuntungan maksimum merupakan aplikasi dari fungsi turunan. Masalah meminimumkan atau memaksimalkan cukup banyak bermanfaat dalam kegiatan produksi sehari-hari.
Contoh masalah meminimumkan terdapat pada bagaimana cara meminimalkan biaya produksi dari suatu usaha. Atau pada kasus bagaimana menghitung banyak hari yang diperlukan agar suatu proyek mendapatkan keuntungan yang maksimum. Bagaimana cara menghitung biaya produksi minimum atau keuntungan maksimum? Sobat idschool dapat mencari tahu lebih lanjut melalui ulasan di bawah.
Table of Contents
- Nilai Maksimum dan Minimum
- Teorema Titik Keberadaan Maksimum-Minimum
- Cara Mendapatkan Nilai Maksimum dan Minimum
- Contoh Soal dan Pembahasan
Nilai Maksimum dan Minimum
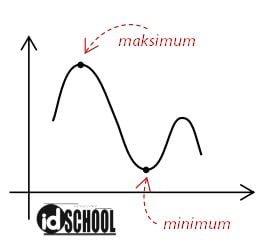
Nilai maksimum suatu fungsi f pada suatu himpunan S adalah nilai f terbesar yang dapat dicapai pada keseluruhan himpunan S. Sedangkan nilai minimum suatu fungsi f pada himpunan S adalah nilai f terkecil yang dapat dicapai pada keseluruhan himpunan S.
Definsi nilai maksimum dan minimum: Misalkan S adalah daerah asal f dan S memuat titik c, sehingga
- f(c) adalah nilai maksimum f pada S jika f(c) ≥ f(x), untuk setiap x Є S, sedangkan f(c) adalah nilai minimum f pada S jika f(c)≤ f(x), untuk setiap x Є S
- f(c) adalah nilai ekstrim f pada S jika f(c) adalah nilai maksimum atau nilai minimum
- Fungsi yang ingin dimaksimumkan atau diminimumkan adalah fungsi objektif
Teorema Titik Keberadaan Maksimum-Minimum
Bahasan keberadaan nilai maksimum dan minimum termuat dalam teorema keberadan maksimum-minimum. Torema: Jika f kontinu pada selang tertutup [a, b] maka f mencapai f mencapai nilai maksimum dan nilai minimum di selang tertutup [a, b].
Berdasarkan teorema tersebut maka f mempunyai nilai maksimum dan minimum dengan syarat f berupa fungsi kontinu dan himpunan S disyaratkan berupa selang tertutup. Kemungkinan tempat letak titik ekstrim (nilai maksimum dan minimum) yaitu dapat terjadi seperti tiga gambar berikut.

Jika c sebuah titik tempat maka kemungkinan tempat terjadinya nilai ekstrim c merupakan salah satu dari titik-titik berikut.
- Ujung interval
- Stasioner dari f → f’(c) = 0
- Singuler dari f → f’(c) tidak ada
Ketiga jenis titik tersebut (ujung interval, stasioner, dan singular) merupakan titik-titik kunci dari teori maksimum-minimum. Cara mendapatkan nilai maksimum atau minimum diperoleh dari substitusi nilai titik-titik tersebut pada fungsi f.
Sebagai contoh, perhatikan bagaimana cara menghitung nilai maksimum dan minimum suatu fungsi f berikut.
Cara Mendapatkan Nilai Maksimum dan Minimum
Soal:
Berapakan nilai maksimum dan minimum dari f(x) = –2x3 + 3x2 pada [–1/2, 2]?
- Mencari turunan pertama dari fungsi f(x): f’(x) = –6x2 + 6x
- Menentukan titik kritis:
f’(x) = 0
–6x2 + 6x = 0
6x(1 – x) = 0
6x = 0 atau 1 – x = 0, diperoleh hasil x = 0 atau x = 1 - Diketahui titik ujung interval adalah –1/2 dan 2, sehingga diperoleh empat titik kritis { –1/2, 0, 1, 2}.
Dari empat titik kritis yang dipeorleh akan digunakan untuk mencari nilai maksimum dan minimum.
- x = –1/2
f(x) = –2x3 + 3x2
f( –1/2) = –2( –1/2)3 + 3( –1/2)2
= –2( –1/8) + 3(1/4)
= 1/4 + 3/4
f( –1/2) =1
- x = 0
f(x) = –2x3 + 3x2
f(0) = –2(0)3 + 3(0)2 = 0
- x = 1
f(x) = –2x3 + 3x2
f(1) = –2( 1)3 + 3(1)2
= –2(1) + 3(1)
= –2 + 3 = 1
- x = 2
f(x) = –2x3 + 3x2
f(2) = –2( 2)3 + 3(2)2
= –2(8) + 3(4)
= –16 +14
f(2) = –4
Berdasarkan perhitungan di atas dapat diperoleh nilai maksimum fungsi f pada [–1/2, 2] adalah 1 dan nilai minimumnya adalah –4.
Selanjutnya, aplikasi dari bahasan turunan di atas dapat digunakan pada cara menghitung biaya minimum produksi atau keuntungan maksimum.
Baca Juga: Aplikasi Turunan untuk Menghitung Luas Maksimum Suatu Daerah
Contoh Soal dan Pembahasan
Beberapa contoh soal cara menghitung biaya produksi minimum di bawah dapat sobat idschool gunakan untuk mengukur pemahaman materi. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan, sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Menghitung Biaya Produksi Minimum

Pembahasan:
Misalkan f(x) adalah fungsi biaya produksi yang dikeluarkan dengan x merupakan banyaknya hari, maka biaya yang dikeluarkan selama x hari adalah sebagai berikut.
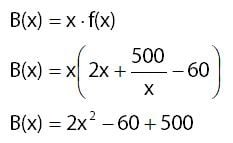
Fungsi biaya yang dikeluarkan B(x) = 2x2 – 60x + 500 akan minimal saat turunan pertamanya sama dengan nol. Selanjutnya, mencari nilai x saat biaya produksi minimum seperti yang dilakukan pada cara berikut.
B(x) = 2x2 – 60x + 500
B’(x) = 4x – 60
4x – 60 = 0
4x = 60
x = 60/4 = 15 hari
Hasil dari perhitungan di atas mememiliki pengertian bahwa biaya produksi minimum saat 15 hari. Sehingga biaya produksi minimum dapat dihitung dengan cara substitusi nilai x = 15 pada persamaan B(X).
Biaya produksi minimum (x = 15):
B(x) = 2x2 – 60x + 500
B(15) = 2(15)2 – 60(15) + 500
= 2 · 225 – 60 · 15 + 500
= 450 – 900 + 500
= 50 juta rupiah
Jadi, biaya produksi minimum untuk sepatu tersebut adalah Rp50.000.000,00.
Jawaban: A
Contoh 2 – Soal Menghitung Banyak Hari agar Biaya Produksi Minimum
Suatu proyek pembangunan gedung sekolah dapat diselesaikan dalam x hari dengan biaya proyek per hari (3x – 720 + 120.000/x) ratus ribu rupiah. Agar biaya proyek minimum, maka proyek tersebut harus diselesaikan dalam waktu ….
A. 60 hari
B. 90 hari
C. 120 hari
D. 150 hari
E. 200 hari
Pembahasan:
Menentukan fungsi biaya B(x) yang dikeluarkan selama x hari pada proyek pembangunan gedung sekolah tersebut:
B(x) = x(3x – 720 + 120.000/x)
B(x) = 3x2 – 720x + 120.000
Fungsi biaya B(x) akan maksimum saat turunan pertamanya sama dengan nol. Waktu pengerjaan proyek (x) tersebut dapat ditentukan melalui persamaan turnanan yang diperoleh.
B(x) = 3x2 – 720x + 120.000
B’(x) = 6x – 720
0 = 6x – 720
6x = 720
x = 720/6 = 120 hari
Jadi, agar biaya proyek minimum maka proyek tersebut harus diselesaikan dalam waktu 120 hari.
Jawaban: C
Contoh 3 – Soal Nilai Maksimum
Selembar seng berbentuk persegi panjang akan dibuat talang air. Agar membentuk talang, kedua tepi seng dilipat sebesar x seperti gambar di bawah.
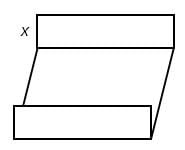
Jika lebar seng adalah 80 cm maka tinggi lipatan talang (x) agar luas penampang talang maksimum adalah ….
A. 20 cm
B. 18 cm
C. 15 cm
D. 10 cm
E. 9 cm
Pembahasan:
Diketahui bahwa lebar seng adalah 80 cm, karena kedua tepinya dilipat sebesar x maka lebar penampang seng menjadi 80 – 2x.
Luas penampang talang L(x) adalah luas lantai talang dikalikan tinggi talang, sehingga fungsi luas penampang talang adalah sebagai berikut.
L(x) = x(80 – 2x)
L(x) = 80x – 2x2
Nilai L(x) akan maksimum saat turunan pertamanya sama dengan nol yaitu L'(x)= 0.
L(x) = 80x – 2x2
L'(x) = 80 – 4x
0 = 80 – 4x
4x = 80
x = 20 cm
Nilai x mewakili tinggi talang, artinya agar luas penampang talang maksimum maka tinggi talang x = 20 cm.
Jawaban: A
Sekian ulasan materi cara menghitung biaya produksi minimum dan keuntungan maksimum dari suatu produksi. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Pengantar Materi Turunan
