Cara Mencari Rata-rata Gabungan 2 Kelompok atau Lebih

Rumus rata-rata gabungan sama dengan jumlah nilai kelompok dibagi banyak data. Misalkan, diketahui siswa kelas A memiliki nilai rata-rata x̄_A dengan banyak siswa n_A. Sementara siswa kelas B memiliki nilai rata-rata x̄_B dengan banyak siswa n_B.

Jumlah nilai siswa kelas A = x̄_A · n_A dan jumlah nilai siswa kelas B = x̄_B · n_B. Rata-rata gabungan kelas A dan B adalah x̄ = (x̄_A · n_A + x̄_B · n_B)/(n_A + n_B).

Penjelasan lebih lanjut cara mencari rata-rata gabungan ada di bawah.

Daftar isi:

• Rumus Rata-Rata Gabungan
• Cara Menghitung Rata-Rata Gabungan
• Contoh Soal dan Pembahasan
  • Contoh 1 – Banyak siswa kelas A adalah …
  • Contoh 2: Rata-rata berat 8 siswa yang baru adalah ….
  • Contoh 3: Rata-rata berat badan kedua anak yang sedang sakit adalah ….

Baca Juga: Rumus Mean, Median, dan Modus Data Kelompok

Rumus Rata-Rata Gabungan

Diketahui ada dua kelompok yang memiliki nilai rata-rata dan banyak data yang berbeda. Jika dua kelompok digabung, nilai rata-ratanya akan berbeda. Nilai rata-rata baru dari kedua kelompok tadi ini yang disebut sebagai rata-rata gabunga.

Misalkan nilai rata-rata dari dua kelompok adalah x̅₁ dan x̅₂. Dan banyak data dari kedua kelompok adalah n₁ dan n₁. Jumlah seluruh data dari dua kelompok ini = x̅₁ · n₁ + x̅₂ · n₂. Sementara banyak data gabungan = n₁ + n₂.

Rumus rata-rata gabungan dari dua kelompok tersebut sama dengan jumlah data dibagi banyak data setelah digabung.

Keterangan:
n₁ = banyak data kelompok pertama
n₂ = banyak data kelompok kedua
x̄₁ = rata-rata kelompok pertama
x̄₂ = rata-rata kelompok kedua

Untuk rata-rata nilai dari k kelompok berturut-turut adalah x̅₁, x̅₂, x̅₃, …, x̅_k. Dengan banyak data setiap kelompok adalah n₁, n₂, n₃, …, n_k. Rumus rata-rata gabungan dari k kelompok dinyatakan melalui persamaan berikut.

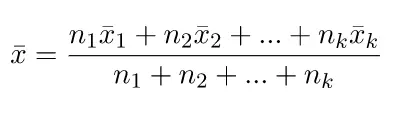
Baca Juga: Cara Menghitung Median Data Kelompok

Cara Menghitung Rata-Rata Gabungan

Untuk mengetahui cara menghitung rata-rata gabungan, akan ditunjukkan melalui sebuah soal. Perhatikan soal di bawah!

Soal:
Rata-rata nilai ulangan 12 siswa laki-laki adalah 72 dan 24 siswa perempuan adalah 80. Rata-rata gabungan nilai siswa laki-laki dan perempuan adalah ….

Jawab:
Dari soal diketahui beberapa informasi berikut.

Banyak siswa laki-laki: n_L = 12
Nilai rata-rata siswa laki-laki: x̅_L = 72

Banyak siswa perempuan: n_p = 24
Nilai rata-rata perempuan: x̅_L = 75

Menghitung rata-rata gabungan:

Jadi, rata-rata gabungan nilai siswa laki-laki dan perempuan adalah 74.

Contoh Soal dan Pembahasan

Lebih banyak soal latihan soal rata-rata gabungan dan pembahasannya ada di bawah.

Contoh 1 – Banyak siswa kelas A adalah …

Nilai rata-rata ujian matematika di kelas A adalah 7. Seseorang mengikuti ujian susulan dan mendapatkan nilai 8,25. Jika rata-rata di kelas A menjadi 7,05 maka banyak siswa dalam kelas A adalah ….
A. 12 siswa
B. 15 siswa
C. 20 siswa
D. 25 siswa

Pembahasan:
Dari keterangan pada soal diperoleh informasi-informasi seperti berikut.

• Rata-rata sebelum ditambah nilai siswa susulan: x̅₁ = 7
• Rata-rata setelah ditambah nilai siswa susulan: x̅₂ = 7,05
• Nilai siswa yang mengikuti ujian susulan = 8,25

Misalkan,
n = banyak siswa di kelas A

Cara menghitung banyak siswa kelas A ada di bawah.

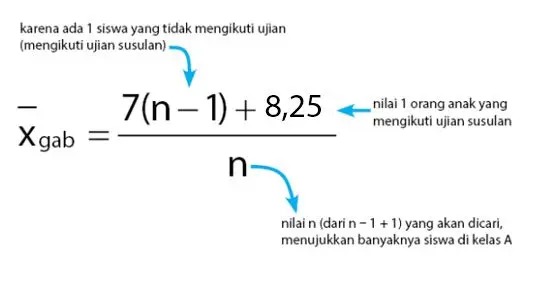
Sehingga,

7,05 n = 7n + 1,25

7,05 n ‒ 7n = 1,25

0,05n = 1,25

Jadi, banyak siswa dalam kelas tersebut adalah 25 siswa.

Jawaban: D

Contoh 2: Rata-rata berat 8 siswa yang baru adalah ….

Sekelompok orang terdiri atas 12 siswa memiliki berat 52 kg. Terdapat 8 siswa lain yang masuk ke kelompok tersebut sehingga rata-rata berat badannya menjadi 48 kg. Rata-rata berat dari 8 siswa yang baru masuk ke kelompok tersebut adalah ….
A. 42 kg
B. 43 kg
C. 44 kg
D. 45 kg

Pembahasan:
Dari soal diperoleh informasi-informasi berikut.

• Banyak orang di kelompok pertama: n₁ = 12
• Rata-rata berat badan kelompok pertama: x₁ = 52
• Banyak orang di kelompok kedua: n₂ = 8
• Rata-rata gabungan kedua kelompok: x_gabungan = 48

Mencari rata-rata berat badan 8 orang siswa yang baru masuk:

48 × 20 = 624 + 8x̅₂

960 = 624 + 8x̅₂

8x̅₂ = 960 ‒ 624 = 336

Jadi, rata-rata berat dari 8 siswa yang baru masuk ke kelompok tersebut adalah 42 kg.

Jawaban: A

Contoh 3: Rata-rata berat badan kedua anak yang sedang sakit adalah ….

Rata-rata berat badan dari 17 anak yang akan mengikuti lomba senam adalah 46,5 kg. Karena sakit, ada dua anak yang tidak bisa mengikuti lomba sehingga menyebabkan rata-rata berat badan turun 1,5 kg.

Rata-rata berat badan kedua anak yang sedang sakit adalah ….
A. 52,75 kg
B. 57,75 kg
C. 62,75 kg
D. 67,75 kg

Pembahasan:
Dari soal diperoleh informasi-informasi seperti berikut.

• Jumlah anak seluruhnya: n = 17
• Banyak anak yang sakit: n₂ = 2
• Banyak anak yang tidak sakit:
  n₁ = 17 ‒ 2 = 15

• Rata-rata seluruh anak: x̄_gabungan = 46,5 kg
• Rata-rata anak yang tidak sakit: x̄₁ = 46,5 ‒ 1,5 = 45 kg

Misalkan,
x̄₂ = rata-rata berat badan dua anak yang tidak jadi mengikuti lomba karena sakit

Menghitung x̄₂:

n ∙ x̄_gabungan = n₁ ∙ x̄₁ + n₂ ∙ x̄₂

17×46,5 = 15×45 + 2×x̄₂

790,5 = 675 + 2x̄₂

2x̄₂ = 790,5 – 675 = 115,5

Jadi, rata-rata gabungan berat badan dari kedua siswa yang tidak jadi mengikuti lomba senam adalah 57,75 kg.

Jawaban: B

Sekian pembahasan nilai rata-rata gabungan dan contoh soalnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Aturan Pengisian Tempat