Cara Mencari Rata-rata Gabungan 2 Kelompok atau Lebih

Rumus rata-rata gabungan digunakan untuk mencari nilai rata-rata dari penggabungan dua kelompok atau lebih. Misalnya, diketahui kelas A memiliki nilai rata-rata X dengan banyak siswa n dan kelas B memiliki nilai rata-rata Y dengan banyak siswa m. Nilai rata-rata nilai dari kelas A dan B dapat dicari tahu dengan rumus rata-rata gabungan.

Nilai rata-rata adalah suatu nilai yang diperoleh dari jumlah semua nilai dibagi banyak data. Untuk kumpulan data sebanyak n dengan nilai-nilai x₁, x₂, x₃, … x_n di mana x_i adalah suatu bilangan real dan n adalah bilangan asli. Nilai rata-rata dapat dihitung dengan rumus x̅ seperti berikut.

Baca Juga: Rumus Mean, Median, dan Modus Data Kelompok

Namun jika diktahui nilai rata-rata dari dua kelompok dengan jumlah data yang berbeda untuk setiap kelompok, bagaimana cara menghitungnya? Melalui halaman ini, sobat idschool dapat mencari tahu bagaimana cara mencari nilai rata-rata gabungan. Contoh cara mencari nilai rata-rata gabungan akan ditunjukkan melalui penyelesaian sebuah soal yang akan diberikan pada akhir bagian.

Rumus Rata-rata Gabungan

Dua kelompok mempunyai sejumlah anggota dan nilai rata-rata yang berbeda. Jika keduanya digabung maka nilai rata-ratanya tentu akan berubah. Nilai rata-rata gabungan dari dua kelompok tersebut bergantung dari banyak data dan rata-rata kelompok pertama serta banyak data dan nilai rata-rata kelompok kedua.

Misalkan ada dua kelompok dengan nilai rata-rata berturut-turut adalah x̅₁ dan x̅₂. Banyak data di kedua kelompok berturut-turut adalah n₁ dan n₁. Nilai rata-rata gabungan dari dua kelompok tersebut memenuhi persamaan berikut.

Keterangan:
n₁ = banyak data kelompok pertama
n₂ = banyak data kelompok kedua
x̄₁ = rata-rata kelompok pertama
x̄₂ = rata-rata kelompok kedua

Dengan menggunakan ide yang sama, rumus rata-rata gabungan juga dapat digunakan untuk mencari rata-rata gabungan dari beberapa kelompok.

Untuk rata-rata nilai dari k kelompok berturut-turut adalah x₁, x₂, x₃, … x_k. Di mana banyak data adalah n₁, n₂, n₃, …, n_k. Rumus rata-rata gabungan dari k kelompok dinyatakan melalui persamaan di bawah.

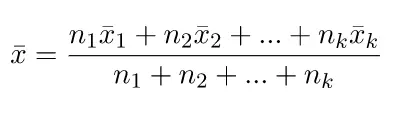
Baca Juga: Cara Menghitung Median Data Kelompok dari Berbagai Bentuk Soal

Contoh Soal Rata – Rata Gabungan dan Pembahasannya

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menguji pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selemat Berlatih!

Contoh 1: Soal Rata – rata Gabungan

Nilai rata-rata ujian matematika di kelas A adalah 7. Seseorang mengikuti ujian susulan dan mendapatkan nilai 8,25. Jika rata-rata di kelas A menjadi 7,05 maka banyak siswa dalam kelas A adalah ….
A. 12 siswa
B. 15 siswa
C. 20 siswa
D. 25 siswa

Pembahasan:
Dari keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• Rata-rata kelompok sebelum ditambah nilai siswa yang mengikuti ujian susulan: x₁ = 7
• Rata-rata kelompok setelah ditambah nilai siswa yang mengikuti ujian susulan: x₂ = 7,05
• Nilai siswa yang mengikuti ujian susulan = 8,25

Misalkan n = banyak siswa di kelas A,
maka dapat diperoleh persamaan di bawah.

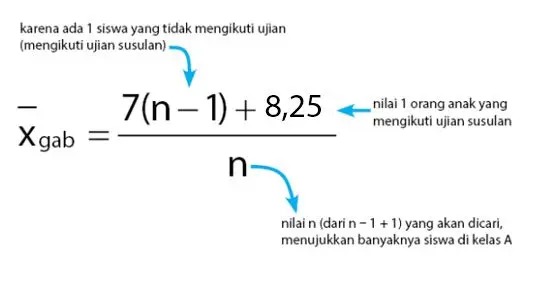
Sehingga, banyaknya siswa di kelas A (n) dapat dihitung seperti lamhkah penyelesaian berikut.

7,05 n = 7n + 1,25
7,05 n ‒ 7n = 1,25
0,05n = 1,25
n = ^1,25/_0,5
n = 25 siswa

Jadi, banyak siswa dalam kelas tersebut adalah 25 siswa.

Jawaban: D

Contoh 2: Soal Rata – rata Gabungan

Sekelompok orang terdiri atas 12 siswa memiliki berat 52 kg. Terdapat 8 siswa lain yang masuk ke kelompok tersebut sehingga rata-rata berat badannya menjadi 48 kg. Rata-rata berat dari 8 siswa yang baru masuk ke kelompok tersebut adalah ….
A. 42 kg
B. 43 kg
C. 44 kg
D. 45 kg

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• Banyak orang pada kelompok pertama: n₁ = 12
• Rata-rata berat badan orang pada kelompok pertama: x₁ = 52
• Banyak orang pada kelompok kedua: n₂ = 8
• Rata-rata gabungan dari kedua kelompok: x_gab. = 48

Mencari rata-rata berat badan 8 orang siswa yang baru masuk:

48 × 20 = 624 + 8x̅₂
960 = 624 + 8x̅₂
8x̅₂ = 960 ‒ 624 = 336
x̅₂ = ³³⁶/₈ = 42 kg

Jadi, rata-rata berat dari 8 siswa yang baru masuk ke kelompok tersebut adalah 42 kg.

Jawaban: A

Contoh 3: Soal Rata – rata Gabungan

Rata-rata berat badan dari 17 anak yang akan mengikuti lomba senam adalah 46,5 kg. Karena sakit, ada dua anak yang tidak bisa mengikuti lomba sehingga menyebabkan rata – rata berat badan turun 1,6 kg. Rata-rata berat badan kedua anak yang sedang sakit adalah ….
A. 52,75 kg
B. 57,75 kg
C. 62,75 kg
D. 67,75 kg

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• banyak anak seluruhnya: n = 17
• jumlah anak yang sakit: n₂ = 2
• banyak anak yang tidak sakit: n₁ = 17 ‒ 2 = 15
• rata-rata untuk seluruh anak: x̄ = 46,5 kg
• rata-rata anak yang tidak sakit: x̄₁ = 46,5 ‒ 1,5 = 45 kg

Misalkan rata-rata berat badan dua anak yang tidak jadi mengikuti lomba adalah x̄₂, maka akan diperoleh persamaan dan penyelesaiannya seperti cara di bawah.

Menghitung nilai rata-rata 2 anak yang sakit (x̄₂):
n ∙ x = n₁ ∙ x̄₁ + n₂ ∙ x̄₂
17 × 46,5 = 15 × 45 + 2 × x̄₂
790,5 = 675 + 2x̄₂
2x̄₂ = 790,5 – 675
2x̄₂ = 115,5
x̄₂ = ^115,5/₂ = 57,75

Jadi, rata-rata gabungan berat badan dari kedua siswa yang tidak jadi mengikuti lomba senam adalah 57,75 kg.

Jawaban: B

Sekian pembahasan mengenai cara mencari rata-rata gabungan yang memuat rumus rata-rata gabungan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Aturan Pengisian Tempat