Fungsi logaritma merupakan bentuk invers dari fungsi eksponen. Bentuk grafik fungsi logaritma adalah kurva yang selalu naik atau selalu turun (grafik monoton). Cara menentukan persamaan fungsi logaritma dari grafik dengan mencari titik-titik koordinat yang dilalui. Lebih lanjut bagaimana cara menentukan persamaan fungsi logaritma dari grafik dijelaskan di bawah.
Daftar isi:
- Fungsi Logaritma
- Grafik Fungsi Logaritma Bentuk Dasar y = alog x
- Grafik Fungsi Logaritma Lainnya
- Contoh Soal dan Pembahasan
Baca Juga: Definisi dan Sifat-Sifat Fungsi Logaritma
Fungsi Logaritma
Fungsi logaritma memiliki bentuk umum y = alog x, di mana a adalah basis (bilangan pokok) logaritma dan x adalah numerus. Di mana numerus adalah bilangan yang dicari nilai logartimnya. Sedangkan hasil dari fungsi logaritma dinyatakan dalam nilai y.
Misalnya, diketahui sebuah fungsi logaritma y = 3log 81. Basis dan numerus dari fungsi logaritma tersebut berturut-turut adalah 3 dan 81. Nilai dari fungsi logaritma tersebut dapat diketahui melalui operasi hitung yang sesuai dengan definisi dan sifat-sifat logaritma yaitu y = 3log 81 = 3log 34 = 4 × 3log 3 = 4 × 1 = 4.
Pasangan nilai-nilai x dan y yang sesuai pada persamaan logaritma y = alog x dapat menghasilkan grafik fungsi logaritma bentuk dasar. Informasi bentuk dasar grafik fungsi logaritma dapat membantu dalam menentukan fungsi logaritma dari grafik. Bagaimana bentuk grafik fungsi logaritma? Bagaimana cara menentukan fungsi logaritma dari grafik? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Grafik Fungsi Logaritma Bentuk Dasar y = alog x
Fungsi logaritma memiliki syarat nilai basis atau bilangan pokok logaritma harus lebih besar dari 0 dan tidak boleh sama dengan 1. Syarat tersebut ada karena fungsi logaritma dengan basis 1 dan 0 tidak memiliki hasil nilai atau tidak terdefinsi.
Nilai basis logaritma (a) pada persamaan logaritma y = f(x) = alog x menjadi penentu bentuk grafik fungsi logritma akan berupa kurva monoton naik atau monoton turun.
- Jika nilai basis logaritma a > 0 maka grafik fungsi logaritma berupa kurva monoton naik.
- Jika basis logaritma berada pada rentang 0 < a < 1 maka grafik fungsi logaritma berupa kurva monoton turun.
Sebagai contoh bentuk dasar fungsi logaritma dengan basis a = 2 dengan persamaan y = 2log x memiliki bentuk kurva monoton naik karena nilai a = 2 > 0. Bentuk grafik fungsi logaritma untuk fungsi y = 2log x sesuai dengan gambar berikut.

Baca Juga: Cara Menggambar Grafik Fungsi Logaritma
Sementara untuk fungsi logaritma dengan basis a = 1/2 dengan persamaan y = ½log x memiliki bentuk kurva monoton turun karena nilai basis logaritma berada pada selang 0 < a < 1. Bentuk grafik fungsi logaritma untuk fungsi y = ½log x sesuai dengan gambar berikut.

Grafik fungsi logaritma y = alog x memiliki sifat selalu memotong sumbu x di titik (1, 0) karena alog 1 = 0. Sedangkan sumbu y merupakan garis asimtot dari fungsi logaritma y = alog x karena alog x mendekati ‒∞ ketika x mendekati 0 dari kanan. Sehingga grafik fungsi logaritma y = alog x tidak memiliki titik potong dengan sumbu y.
Grafik Fungsi Logaritma Lainnya
Grafik fungsi logaritma bentuk dasar di atas dapat mengalami pergeseran atau perubahan kelengkungan kurva. Perubahan yang terjadi dapat disebabkan karena penambahan atau pengurangan konstanta. Perubahan bentuk fungsi logaritma dasar dapat juga berubah karena perkalian dengan suatu konstanta.
1) Pengaruh Penambahan Konstanta
Fungsi logaritma dari grafik bentuk dasar y = alog x yang bergeser ke atas sebanyak c satuan akan memiliki persamaan y = alog x + c. Sedangkan fungsi logaritma dari grafik bentuk dasar y = alog x yang bergeser ke bawah sebanyak c satuan memiliki persamaan y = alog x ‒ c.
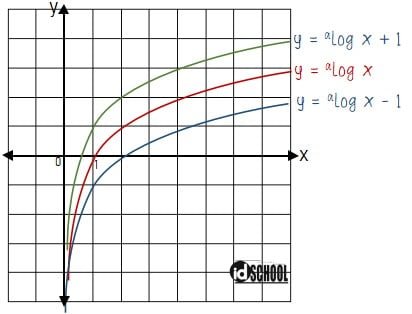
2) Pengaruh Perkalian Konstanta
Perkalian konstanta k pada suatu fungsi logaritma akan membuat kurva dari grafik fungsi logaritma berubah. Untuk nilai k positif (k > 0) tidak akan merubah arah monoton kurva, sementara untuk nilai k negatif (k < 0) akan merubah arah monoton kurva.
Setiap perkalian konstanta dengan fungsi logaritma tidak merubah titik potong kurva dengan sumbu x. Di mana perpotongan titik kurva dengan sumbu x berada di titik (1, 0) karena nilai alog 1 = 0. Gambaran perubahan grafik fungsi kuadrat karena perkalian konstanta fungsi logaritma ditunjukkan seperti berikut.
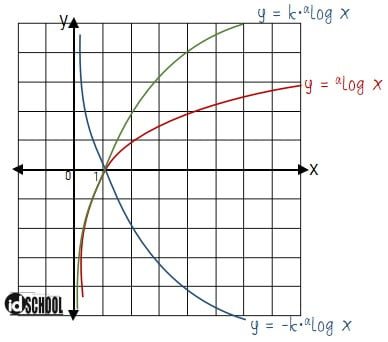
Baca Juga: Himpunan Penyelesiaan Persamaan Logaritma
Contoh Soal dan Pembahasan
Latihan soal menentukan persamaan grafik fungsi logaritma dari grafik ada di bawah!
Contoh 1
Perhatikan gambar berikut!

Fungsi logaritma dari grafik di atas adalah ….
A. y = 3log x
B. y = 2log x
C. y = log x
D. y = ½log x
E. y = ⅓log x
Pembahasan:
Dari grafik fungsi logaritma diketahui kurva melalui titik (1, 0). Perkiraan fungsi logaritma dari grafik adalah y = alog x.
Dari kurva juga dapat diketahui dua titik koordinat yang dilalui yaitu (4, 2) dan (8, 3). Substitusi salah satu titik ke persamaan dapat diperoleh nilai basis yang sesuai untuk grafik fungsi logaritma tersebut.
Mencari nilai basis (a):
y = alog x
2 = alog 4
a2 = 4
a = √4 = ±2
Nilai a yang memenuhi adalah a = 2 karena basis fungsi logaritma memiliki syarat lebih dari nol. Jadi, fungsi logaritma dari grafik di atas adalah y = 2log x.
Jawaban: B
Contoh 2

Persamaan yang sesuai dengan fungsi logaritma dari grafik di atas adalah ….
A. y = 2log x ‒ 1
B. y = 2log x + 1
C. y = 2log (x ‒ 1)
D. y = 2log (x + 1) ‒ 1
E. y = 2log (x + 1) + 1
Pembahasan:
Dari grafik dapat diketahui beberapa titik koordinat yang dilalui kurva yaitu (0, ‒1); (1, 0); dan (3, 1). Pada pilihan yang diberikan diketahui bahwa semua basis fungsi logaritma adalah 2 sehingga dapat dibentuk pemisalan fungsi logaritma y = 2log (x + a) + b. Sehingga akan diperoleh tiga persamaan berikut.
- Untuk (0, ‒1):
y = 2log (x + a) + b
‒1 = 2log (0 + a) + b
- Untuk (1, 0):
0 = 2log (1 + a) + b
b = ‒2log (1 + a)
- Untuk (3, 1):
1 = 2log (3 + a) + b
1 ‒ b = 2log (3 + a)
Substitusi b = ‒2log (1 + a) pada persamaan ‒1 = 2log a + b untuk mendapatkan nilai a seperti pada penyelesaian berikut.
‒1 = 2log a + b
‒1 = 2log a ‒ 2log (1 + a)
‒2log 2 = 2log a/1+a
2log 2‒1 = 2log a/1+a
1/2 = a/1+a
2a = 1 + a
2a ‒ a = 1
a = 1
Untuk mendapatkan nilai b, subtitusi nilai a = 1 ke persamaan b = ‒2log (1 + a):
b = ‒2log (1 + 1)
b = ‒2log 2 = ‒1
Sebelumnya dimisalkan persamaan logaritma yang sesuai dengan grafik adalah y = 2log (x + a) + b = 2log (x + 1) ‒1. Jadi, persamaan grafik fungsi di atas adalah y = 2log (x + 1) ‒ 1.
Jawaban: D
Demikianlah tadi cara menentukan fungsi logaritma dari grafik. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Contoh Soal Logaritma HOTS dan Pembahasannya
