Gaya tarik antara partikel-partikel bermassa tersebut disebut dengan gaya gravitasi, seperti pada gaya tarik antara Matahari dan Bumi. Besar gaya gravitasi antara dua benda bermuatan dengan massa m1 dan m2 dapat dihitung dengan rumus F = GMm/R2. Di mana G adalah konstanta gravitas bumi yang nilainya mendekati g = 10 m/s2, M dan m adalah massa benda pertama dan kedua, sedangkan R adalah jarak antara dua benda.
Sebuag teori yang disampaikan Issac Newton dan Kepler menyatakan bahwa antara planet dengan planet atau antara matahari dengan planet memiliki gaya tarik-menarik. Gaya tarik menarik benda-benda di alam semesta seperti planet dan matahari disebut dengan gaya gravitasi semesta.
Pada daerah sekitar gaya gravitasi antara dua benda dengan massa m1 dan m2 terdapat ruang yang dipengaruhi gaya tersebut. Ruang yang masih dipengaruhi oleh gaya gravitasi disebut medan gravitasi, di mana besarnya sama dengan gaya gravitasi setiap satuan massa.
Dua benda yang bermassa m1 dan m2 mempunyai jarak antara pusat massanya adalah R. Kedua benda saling tarik-menarik dengan gaya gravitasi F yang besarnya berbanding lurus dengan massa masing-masing benda dan berbanding terbalik dengan kuadrat jarak antara pusat massanya. Besar gaya gravitasi antara dua benda dengan massa m1 dan m2 dapat dihitung melalui persamaan di bawah.

Baca Juga: Hukum Gravitasi Newton
Bagaiaman cara menghitung gaya gravitasi antara dua benda bermuatan dengan massa m1 dan m2? Bagaimana besar pengaruh gaya gravitasi antara dua benda yang saling berintaraksi? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Konstanta Gravitasi Umum (G)
- Medan Gravitasi
- Gaya Gravitasi Antara Dua Benda dengan Massa m1 dan m2
- Contoh Soal dan Pembahasan
- Contoh 1 – Soal Gaya Gravitasi Antara Dua Benda dengan Massa m1 dan m2
Konstanta Gravitasi Umum (G)
Konstanta gravitasi umum (G) merupakan sebuah tetapan yang nilainya sama dengan G = 6,673 x 10–11 Nm2/kg2. Nilai G tersebut diukur dengan sebuah alat yang disebut dengan neraca torsi atau neraca puntir. Sir Henry Cavendish adalah tokoh yang pertama kali menggunaakn neraca tersebut pada tahun 1798. Neraca torsi atau neraca puntir tersebut kemudian dikenal dengan neraca Cavendish.
Neraca Cavendish terdiri atas batang ringan berbentuk huruf T yang diikat dengan benang halus. Dua buah bola kecil yang masing-masing bermassa m1 diletakkan pada ujung-ujung batang yang mendatar. Pada batang yang tegak diletakkan sebuah cermin M untuk memantulkan seberkas cahaya pada skala.
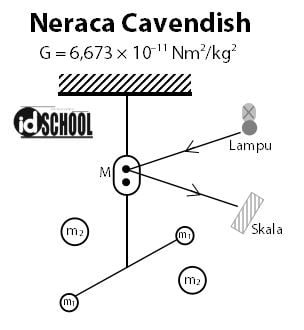
Cara menggunakan alat tersebut adalah dengan meletakkan dua bola dengan massa m2 pada kedudukan tertentu (seperti pada gambar di atas). Dengan memperhatikan sudut simpangan yang ditunjukkan dengan simpangan berkas cahaya yang dipantulkan oleh cermin pada skala dapat diperoleh nilai G = 6,673 × 10–11 Nm2/kg2.
Baca Juga: Cara Menghitung Kecepatan Peluru yang Menumpuk Ayunan Balistik
Medan Gravitasi
Pada benda dengan massa m1 dan m2 yang terletak sejauh R mempunyai besar gaya gravitasi yang dapat dihitung melalui persamaan F. Benda dapat merasakan gaya gravitasi karena pengaruh kuat medan gravitasi. Besarnya gaya persatuan massa yang dirasakan benda dinyatakan melalui persamaan medan gravitasi (g).

Baca Juga: Gerak Benda Jatuh Bebas dan Vertikal ke Atas
Gaya Gravitasi Antara Dua Benda dengan Massa m1 dan m2
Kuat medan magnet membuat benda disekitar gaya gravitasi antara dua benda dapat dirasakan benda disekitarnya. Sebagai contoh, benda m3 berada di sekitar pengaruh gaya gravitasi dua benda m1 dan m2.
Besar gaya gravitasi yang dialami oleh benda m3 merupakan resultan vektor dari gaya gravitasi F1 dan F2. Di mana F1 adalah gaya gravitasi antara benda m1 dan m3. Sedangkan F2 adalah gaya gravitasi antara benda m2 dan m3.

Perhatikan bagaimana cara mendapatkan gaya gravitasi yang dialami oleh benda ketiga (m3) pada soal berikut.
Soal:
Tiga buah benda homogen A, B, dan C memiliki massa berturut-turut 2 kg, 3 kg, dan 4 kg. Ketiga benda terletak pada titik-titik sudut segitiga sama sisi yang panjang sisinya 2 m. Berapakah gaya gravitasi yang dialami benda B?
Penyelesaian:
Gambaran letak kedudukan ketiga benda tersebut diberikan seperti berikut.
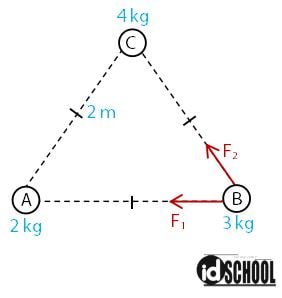
Menghitung gaya gravitasi antara dua benda bermuatan untuk A dan B (FAB) dan gaya gravitasi antara benda C dan B (FCB).
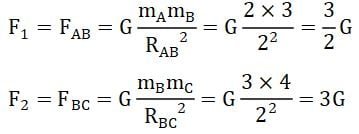
Menghitung gaya gravitasi yang dialami benda B (FR):

Substitusi nilai G = 6,673 × 10–11N sehingga diperoleh nilai seperti berikut.

Jadi, besar gaya gravitasi yang dialami benda C adalah 3/2G√7 N atau sekitar 2,653 × 10–10 N.
Baca Juga: Hubungan Rumus Usaha dan Energi (Kinetik dan Potensial)
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara menghitung gaya gravitasi antara dua benda. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Gaya Gravitasi Antara Dua Benda dengan Massa m1 dan m2
Besar gaya gravitasi dua buah benda adalah F. Jika jarak antara kedua benda diperkecil menjadi seperempat maka besar gaya gravitasi berubah menjadi ….
A. 16 F
B. 8 F
C. 4 F
D. 1/4 F
E. 1/16 F
Pembahasan:
Menentukan besar gaya gravitasi antara dua benda setelah jarak diperkecil menjadi seperempat.

Jadi, besar gaya gravitasi berubah menjadi 16 F.
Jawaban: A
Contoh 2 – Besar dan Arah Resultan Gaya Gravitasi Antara Dua Benda dengan Massa m1 dan m2
Perhatikan gambar di bawah ini!
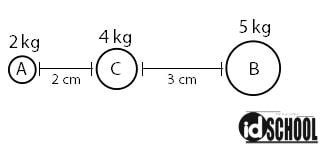
Besar dan arah resultan gaya gravitasi pada massa C adalah …. (G = 6,67 × 10–11 N)
A. 17,78 × 10–7 N ke kanan
B. 13,34 × 10–7 N ke kiri
C. 4,47 × 10–7 N ke kanan
D. 3,20 × 10–7 N ke kiri
E. 1,48 × 10–7 N ke kanan
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Massa benda A, B, dan C: mA = 2 kg, mB = 5 kg, dan mC = 4 kg
- Jarak benda A ke benda C: RA = 2 cm = 2 × 10–2 m
- Jarak benda B ke benda C: RB = 3 cm = 3 × 10–2 m
- Konstanta gravitasi: G = 6,67 × 10–11 N
Menghitung gaya gravitasi antara dua benda atau gaya gravitasi yang dialami benda C karena pengaruh benda A dan B. Di mana besar gaya gravitasi antara dua benda disimbolan dengan FA (karena pengaruh benda C) dan FB (karena pengaruh benda B).

Besar FB lebih besar dari FA (FB > FA) sehingga gaya gravitasi pada benda C (FC) akan mengarah ke benda B (ke kanan). Besar gaya FC merupakan resultan dari gaya FA dan FB.
FC = FB – FA
FC = 20/9G×104 – 2G×104
= 20/9G×104 – 18/9G×104
= 2/9G×104 N
Substirusi nilai konstata gravitasi G = 6,67 × 10–11 N:
FC = 2/9 × 6,67 × 10–11 ×104 N
= 1,48 × 10–7
Jadi, besar dan arah resultan gaya gravitasi pada massa C adalah 1,48 × 10–7 N ke kanan.
Jawaban: E
Contoh 3 – Perbandingan Berat Benda pada Tempat dengan Gravitasi Berbeda
Planet X massanya 3 kali massa bumi dan jari-jarinya 11/2 jari-jari bumi. Jika sebuah benda di permukaan bumi beratnya w maka berat benda tersebut di permukaan planet X adalah ….
A. 1/3 w
B. 2/3 w
C. 3/4 w
D. 4/3 w
E. 4 w
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Misalkan:
massa bumi = mB
jari-jari Bumi = rB - Massa Planet X: mX = 3 mB
- Jari-jari planet X: rX = 11/2 rB
- Beran benda di permukaan bumi: wB = w
Berat benda tersebut di permukaan planet X:
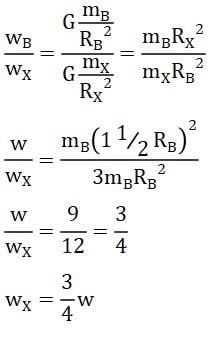
Jadi, berat benda tersebut di permukaan planet X adalah 3/4 w.
Jawaban: C
Contoh 4 – Soal Gaya Gravitasi Dua Benda
Jarak antara Matahari dan Bumi adalah 1,5 × 108 km, sedangkan jarak antara Matahari dan Neptunus adalah 4,5 × 109 km. Periode Neptunus mengelilingi Matahari adalah 165 tahun dan massa Neptunus adalah 18 kali massa Bumi. Jika besar gaya gravitasi pada Bumi oleh Matahari adalah F dan kelajuan Bumi mengelilingi Matahari adalah v, gaya gravitasi pada Neptunus oleh Matahari serta kelajuan Neptunus adalah ….
A. F/10 dan v/11
B. F/50 dan 2v/11
C. F/100 dan 2v/55
D. F/50 dan v/55
E. 3F/100 dan 3v/55
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh beberapa informasi seperti berikut.
- Jarak Matahari dan Bumi: rB = 1,5 × 108 km
- Jarak Matahari dan Neptunus: rN = 4,5 × 109 km
- Jari-jari Neptunus: rN = 30 rB
- Periode Neptunus mengelilingi Matahari: TN = 165 tahun
- Massa Neptunus adalah 18 kali massa bumi: mN = 18 mB
- Gaya gravitasi Bumi = F
- Kelajuan Bumi mengelilingi Matahari = v
Perbandingan gaya gravitasi Newton dengan Bumi:

Perbandingan kecepatan orbit Bumi dengan Neptunus:

Jadi, gaya gravitasi pada Neptunus oleh Matahari serta kelajuan Neptunus adalah F/50 dan 2v/11.
Jawaban: B
Demikianlah tadi ulasan gaya gravitasi antara dua benda bermuatan dengan massa m1 dan m2 atau lebih. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Tegangan Tali yang Menarik Suatu Benda
