Persamaan Bernoulli merupakan bentuk matematis yang sesuai dengan Hukum Bernoulli. Dalam Hukum Bernoulli menerangkan bahwa kenaikan kecepatan aliran dari fluida mampu menyebabkan adanya penurunan tekanan fluida secara bersamaan. Bahasan umum dalam hukum dan persamaan Bernoulli terkait dengan bagaimana perilaku gerak fluida atau yang biasa disebut fluida dinamis. Fluida adalah zat yang bisa mengalir, zat tersebut dapat berupa zat lelehan, cair, atau zat gas.
Fluida bergerak mengalir dalam sebuah pipa yang ketinggian dan luas penampangnya yang berbeda. Adanya aliran fluida disebabkan karena perbedaan tekanan kedua ujung pipa. Seberapa besar perubahan kecepatan fluida dan perbedaan nilai besaran yang memengaruhi lainnya dapat dicari tahu melalui persamaan Bernoulli.
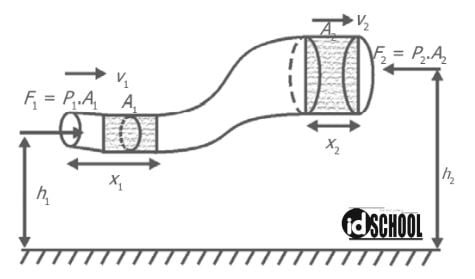
Pada awalnya, fluida memasuki pipa pada penampang A1 dan ketinggian h1 dengan kecepatan v1. Kecepatan fluida mengalami perubahan menjadi v2 ketika berada pada pipa dengan penampang A2 dan ketinggian h2 .
Hukum Bernoulli membahas hubungan antara kecepatan aliran fluida, ketinggian, dan tekanan dengan menggunakan konsep usaha dan energi. Bagaimana bentuk persamaan Bernoulli? Bagaimana hubungan antara kecepatan aliran fluida, ketinggian, dan tekanan pada persamaan Bernoulli? Sobat idschool dapat mencari tahu jawabannya melaui ulasan hukum dan persamaan Bernoulli di bawah.
Table of Contents
Baca Juga: Hukum Kekekalan Momentum
Hukum Bernoulli
Fluida mengalir dari penampang A1 ke ujung pipa dengan penampang A2 karena adanya perbedaan tekanan kedua ujung pipa. Menurut Bernoulli, suatu fluida yang bergerak mengubah energinya menjadi tekanan. Atau dapat dikatakan bahwa gerak fluida berlaku hukum kekekalam energi.
Hukum Bernoulli menyatakan bahwa jumlah tekanan, energi kinetik per satuan volume, dan energi potensial per satuan volume memiliki nilai yang sama di setiap titik sepanjang aliran fluida ideal.
Misalkan, massa jenis fluida ρ, laju aliran fluida pada penampang A1 adalah v1, dan laju aliran fluida pada penampang A2 adalah v2. Bagian fluida sepanjang x1 = v1 ⋅t bergerak ke kanan oleh gaya F1 = P1⋅A1 yang ditimbulkan tekanan P1. Setelah selang waktu t sampai pada penampang A2 sejauh x2 = v2⋅t. Sehingga,
- Besar usaha oleh gaya F1:
W1 = +F1⋅x1 = P1⋅A1⋅x1
- Besar usaha oleh gaya F2:
W2 = –F2⋅x2 = –P2⋅A2⋅x2 (tanda negatif menunjukkan gaya F2 berlawanan dengan arah gerak fluida)
Sehingga usaha total yang dilakukan adalah,

W adalah usaha total yang dilakukan pada bagian fluida yang volumenya V=A1⋅x1 =A2⋅x2 yang akan menjadi tambahan energi mekanik total pada bagian fluida tersebut.
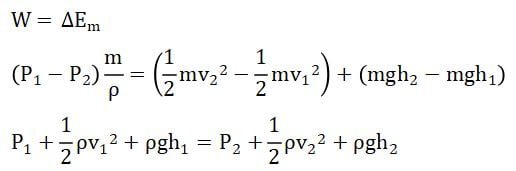
Atau di setiap titik pada fluida yang bergerak berlaku: p + 1/2ρv2 + ρgh = konstan. Ringkasnya, bentuk persamaan Bernoulli diberikan seperti rumus berikut.

Baca Juga: Hukum Bernoulli pada Gaya Angkat Sayap Pesawat
Penerapan Persamaan Bernoulli
Hukum Bernoulli diterapkan dalam berbagai peralatan yang digunakan dalam kehidupan sehari-hari. Persamaan Bernoulli dapat digunakan untuk mengetahui kecepatan fluida dari alat yang menerapkan Hukum Bernoulli. Beberapa alat yang menerapkan Hukum Bernoulli disebutkan seperti daftar berikut.
1. Venturimeter
Venturimeter atau alat ukur venturi dipasang dalam suatu pipa aliran untuk mengukur laju aliran suatu fluida. Pipa venturimeter dibuat dengan kedua ujung yang memiliki luas penampang berbeda.
Fluida dengan massa jenis ρ mengalir masuk melalui pipa dengan luas penampang A1 dan keluar pipa dengan luas penampang A2 yang lebih kecil. Suatu tabung manometer atau pipa U berisi zat cair dengan massa jenis ρ’ dipasang pada pipa. Kecepatan aliran zat cair di dalam pipa dapat diukur dengan persamaan v berikut.

2. Tabung Pitot
Tabung pitot digunakan untuk mengukur kelajuan aliran suatu gas di dalam sebuah pipa. Pipa pitot dilengkapi dengan manometer yang salah satu kakinya tegak lurus aliran fluida sehingga kelajuan gas pada titik tersebut adalah nol.
Dengan kecepatan sama dengan nol pada titik tersebut dapat ditentukan kelajuan udara pada pipa. Udara mengalir melalui tabung A dengan kecepatan v yang dapat dihitung melalui persamaan berikut.

3. Alat Penyemprot Nyamuk
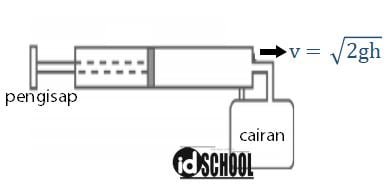
Berdasarkan Hukum Bernoulli, tempat dengan kecepatan semakin besar memiliki tekanan yang semakin kecil. Cara menggunakan alat penyemprot nyamuk dengan memberi tekanan pada bagian pengisap.
Saat bagian pengisap ditekan, udara keluar dengan cepat melalui lubang sempit pada ujung pompa. Akibatnya, tekanan udara pada bagian atas penampung lebih kecil daripada tekanan udara pada permukaan cairan dalam penampung.
Adanya perbedaan tekanan akan membuat cairan bergerak naik dan tersembur keluar dalam bentuk kabut bersama semburan udara pada ujung pompa.
Baca Juga: Hukum Kepler – Periode Revolusi Planet
4. Gaya Angkat pada Sayap Pesawat Terbang
Penampang sayap pesawat terbang mempunyai bagian belakang yang lebih tajam dan sisi bagian atas lebih melengkung daripada sisi bagian bawah. Bentuk ini membuat kecepatan aliran udara melalui sisi bagian atas pesawat (v1) lebih besar daripada kecepatan aliran udara di bagian bawah sayap (v2).
Sesuai Hukum Bernoulli, tempat yang mempunyai kecepatan lebih tinggi akan memiliki tekanan yang lebih rendah. Sehingga, tekanan di atas pesawat (P1) lebih kecil dari tekanan di bawah sayap pesawat (P2).

Selisih tekanan antara sisi atas dan bawah sayap inilah yang menimbulkan gaya angkat pada sayap pesawat. Jika luas penampang sayap pesawat adalah A, maka gaya angkat yang dihasilkan adalah F = 1/2ρA(v12 – v22).
5. Kebocoran pada Dinding Tangki
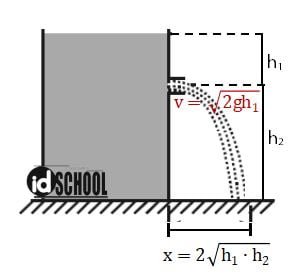
Sebuah tangki mengalami kebocoran pada bagian didingnya dengan panjang diameter sangat kecil dibanding diameter tangki. Kelajuan air yang keluar dari lubang bocor tersebut sama dengan kelajuan yang diperoleh jika air tersebut jatuh bebas dari ketinggian h (Hukum Toricelli).
Misalkan, sebuah tangki dengan ketinggian h mengalami kebocoran pada bagian dinding. Jarak permukaan air yang berada di dalam tangki ke lubang kebocoran dinyatakan sebagai h1, sedangkan jarak lubang kebocoran ke dasar tangki dinyatakan h2. Kecepatan aliran air (v) pada saat keluar dari lubang dan jarak horizontal (x) yang dapat dicapaidapat diketahui melalui hukum Bernoulli.
Baca Juga: Penerapan Hukum Archimedes dalam Kehidupan Sehari-Hari
Contoh Soal Persamaan Bernoulli dan Pembahasan
Selanjutynya, beberapa contoh soal di bawah dapat sobat idschool gunakan untuk melihat bagaimana penggunaan persamaan Bernoulli untuk menyelesaikan soal. Setiap contoh soal yang diberikan di bawah telah dilengkapi dengan pembahasan cara penggunaan persamaan Bernoulli. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Penggunaan Persamaan Bernoulli
Perhatikan aliran fluida melalui pipa berikut ini!

Jika massa jenis fluida 500 kg/m3 maka perbedaan tekanan antara kedua penampang adalah ….
A. 32 kPa
B. 31 kPa
C. 27 kPa
D. 21 kPa
E. 11 kPa
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Massa jenis fluida: ρ = 500 kg/m3
- Perbedaan ketinggian pipa:
∆h = 2 m
h2 – h1 = –2 m
- Kecepatan masuk pipa: v1 = 4 m/s
Kecepatan keluar pipa: v2 = 10 m/s
Perbedaan kecepatan:
∆v2 = v22 – v12
∆v2 = 102 – 42
∆v2 = 100 – 16 = 84 m/s
Persamaan Bernoulli:
P1 + 1/2⋅ρ⋅v12 + ρ⋅g⋅h1 = P2 + 1/2⋅ρ⋅v22 + ρ⋅g⋅h2
P1 – P2 = 1/2⋅ρ⋅v22 + ρ⋅g⋅h2 – (1/2⋅ρ⋅v12 + ρ⋅g⋅h1)
P1 – P2 = 1/2ρ(v22 – v12) + ρg(h2 – h1)
∆P = 1/2ρ(v22 – v12) + ρg(h2 – h1)
Menghitung besar perbedaan tekanan antara kedua penampang:
∆P = 1/2×500×(102 – 42) + 500×10×(–2)
∆P = 1/2×500×84 + 500×10×(–2)
∆P = 21.000 – 10.000 = 11 000 Pa = 11 kPa
Jadi, perbedaan tekanan antara kedua penampang adalah 11 kPa.
Jawaban: E
Contoh 2 – Soal Menghitung Kecepatan Air pada Salah Satu Ujung Pipa dengan Persamaan Bernoulli
Perhatikan gambar berikut!

Posisi pipa besar adalah 5 m di atas tanah dan pipa kecil 1 m di atas tanah. Kecepatan aliran air pada pipa besar adalah 36 km/jam dengan tekanan 9,1×105 Pa, sedangkan tekanan di pipa yang kecil 2×105 Pa. Besar kecepatan air pada pipa kecil adalah …. (massa jenis air = 103 kg/m3 dan percepatan gravitasi = 10 m/s2)
A. 10 m/s
B. 20 m/s
C. 30 m/s
D. 40 m/s
E. 50 m/s
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh beberapa nilai besaran seperti berikut.
- Ketinggian pipa besar: h1 = 5 m
- Ketinggian pipa kecil: h2 = 1 m
- Kecepatan aliran air pada pipa besar: v1 = 36 km/jam = 10 m/s
- Tekanan air pada pipa besar: P1 = 9,1 × 105 Pa
- Tekanan di pipa yang kecil: P2 = 2 × 105 Pa
- Massa jenis air = 103 kg/m3
Menghitung kecepatan air pada pipa kecil:
P1 + 1/2⋅ρ⋅v12 + ρ⋅g⋅h1 = P2 + 1/2⋅ρ⋅v22 + ρ⋅g⋅h2
⇨ 9,1×105 + 1/2×103×102 + 103×10×5 = 2×105 + 1/2×103×v22 + 103×10×1
⇨ 9,1×105 + 0,5×105 + 0,5×105 = 2×105 + 500v22 + 0,1×105
500v22 = 9,1×105 – 2×105 + 0,5×105 + 0,50 ×105 – 0,1×105
500v22 = 8×105
v22 = 800.000/500
v22 = 1.600 → v2 = 40 m/s
Jadi, besar kecepatan air pada pipa kecil adalah 40 m/s.
Jawaban: D
Contoh 3 – Soal Persamaan Bernoulli untuk Menghitung Tekanan Air pada Salah Satu Ujung Pipa
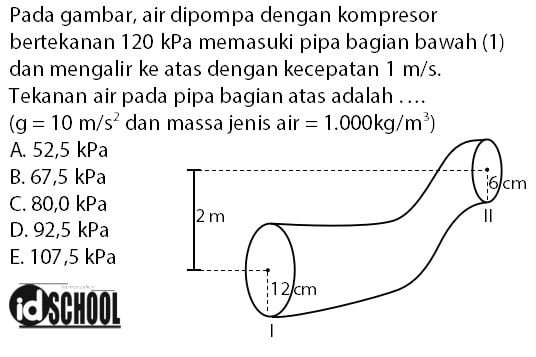
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Tekapan pada pipa bagian bawah (I): P1 = 120 kPa
- Kecepatan aliran air pada pipa bawah: v1 = 1 m/s
- Jari-jari pipa bawah (I): r1 = 12 cm = 0,12 m
- Jari-jari pipa atas (II): r2 = 6 cm = 0,06 m
- Percepatan gravitasi: g = 10 m/s2
- Massa jenis air: ρair = 1.000 kg/m3
- Perbedaan ketinggian pipa I dan II: ∆h = h2 – h1 = 2 m
Menentukan besar kecepatan aliran air pada pipa bagian atas/pipa II (v2):
A1⋅ v1 = A2⋅v2
(πr12) × v1 = (πr22) × v2
r12 × v1 = r22 × v2
0,122 × 1 = 0,062 × v2
0,0144 = 0,0036v2
v2 = 0,0144/0,0036 = 4 m/s
Menghitung tekanan air pada pipa bagian atas (P2):
P1 + 1/2⋅ρ⋅v12 + ρ⋅g⋅h1 = P2 + 1/2⋅ρ⋅v22 + ρ⋅g⋅h2
P1 – P2 = 1/2ρ(v22 – v12) + ρg(h2 – h1)
120 kPa – P2 = 1/2× 1. 000 × (42 – 12) + 1.000 × 10 × 2
120.000 Pa – P2 = 27.500 Pa
P2 = 120.000 Pa – 27.500 Pa
P2 = 92.500 Pa = 92,5 kPa
Jadi, tekanan air pada pipa bagian atas adalah 92,5 kPa.
Jawaban: D
Demikianlah tadi ulasan persamaan Bernoulli dan contoh soal beserta pembahasan cara penggunaan persamaan Bernoulli. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Hukum Newton I, II, dan III
