Himpunan atau set adalah kumpulan objek-objek yang dapat difinisikan dengan jelas. Hubungan himpunan dengan himpunan menyetakan relasi dari dua himpunan atau lebih. Bentuk hubungan himpunan dengan himpunan dapat berupa himpunan bagian, ekivalen, sama, saling lepas, dan berpotongan.
Objek-objek dalam himpunan disebut sebagai anggora atau elemen dari himpunan tersebut. Notasi himpunan dinyatakan dalam huruf kapital seperti A, B, C, dan lain sebagainya. Anggota suatu himpunan dapat dituliskan dengan diapit kurung kurawal dan setiap anggota himpunan dipisahkan dengan tanda koma. Contoh penulisan himpunan: A = {a, b, c, d, e}; B = {1, 2, 3, 4, 5, 6, 7}; C = {2, 3, 5, 7, 11}; dan lain sebagainya.
Baca Juga: Himpunan dan Diagram Venn
Perhatikan himpunan B dan himpunan C memiliki beberapa anggota himpunan yang sama. Sehingga antara himpunan B dan C memiliki suatu hubungan. Apa hubungan yang dimiliki antara himpunan B dengan himpunan C? Bagaimana cara menyatakan hubungan himpunan dengan himpunan? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Himpunan Bagian (Subset)
- Himpunan Kuasa (Superset)
- Himpunan Ekivalen (~)
- Sama Dengan (=)
- Himpunan Lepas (ǁ)
- Contoh Soal Hubungan Himpunan dengan Himpunan dan Pembahasannya
Himpunan Bagian (Subset)
Simbol himpunan bagian ditulis dengan ⊂yang artinya setiap anggota A juga merupakan anggota B. Misalnya diketahui himpunan A = {2, 3, 5} dan B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Setiap anggota himpunan A terdapat merupakan anggota himpunan B. Sehingga dapat dikatakan bahwa himpunan A merupakan himpunan bagian B atau A subset B (A⊂B).
Setiap anggota himpunan A juga merupakan anggota himpunan B. Jika ada satu saja anggota himpunan yang tidak menjadi anggota himpunan lain maka tidak terdapat hubungan himpunan bagian (⊄).
Bagan di bawah merupakan digaram venn yang menggambarkan hubungan himpunan yang merupakan subset dan bukan subset.
Baca Juga: Cara Menentukan Banyaknya Anggota Himpunan Bagian
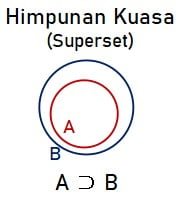
Himpunan Kuasa (Superset)
Himpunan kuasa ata superset merupakan kebalikan dari himpunan bagian. Simbol dari himpunan kuasa adalah pencerminan dari simbol himpunan bagian yaitu ⊃ (superset). Himpunan A superset B (A ⊃ B) jika setiap anggota B juga merupakan anggota A.
Sebagai contoh, terdapat himpunan A = {1, 2, 3, 4, 5, 6, 7, 8} dan B = {1, 3, 5}. Jadi hubungan antara himpunan A dan B adalah himpunan kuasa atau superset. Digaram venn yang menggambarkan hubungan himpunan dengan himpunan yang merupakan himpunan kuasa adalah sebagai berikut.
Baca Juga: Opersai pada Himpunan
Himpunan Ekivalen (~)
Simbol untuk dua himpunan ekivalen dihubungkan oleh tanda ~. Dua himpunan merupakan himpunan ekivalen jika banyak anggota dari kedua himpunan adalah sama. Misalnya banyak anggota himpunan A sama dengan banyak anggota himpunan B maka dapat dituliskan A ~ B.
Banyak himpunan A dituliskan dengan n(A) dan banyak himpunan B dituliskan dengan n(B). Sehingga A~B bila dan hanya bila n(A) = n(B).
Contoh dua himpunan ekivalen adalah A = {a, b, c, d, e} dan B = {1, 2, 3, 4, 5}. Diketahui bahwa n(A) = 5 dan n(B) = 4 sehingga hubungan himpunan A dan B adalah himpunan ekivalen (A ~ B).
Sama Dengan (=)
Himpunan A dikatakan sama dengan himpunan B jika setiap anggota himpunan A sama dengan himpunan B. Dengan kata lain, himpunan A sama dengan himpunan B jika setiap anggotanya sama. Persamaan bukan hanya pada jumlah anggota namun juga anggota-anggota himpunan.
Simbol dua himpunan yang memiliki hubungan sama dengan adalah = (sama dengan). Misalnya diketahui himpunan A = {a, b, c, d} dan B = {d, c, b, a}. Hubungan kedua himpunan tersebut adalah sama dengan (A = B).
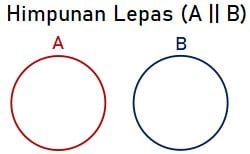
Himpunan Lepas (ǁ)
Himpunan A dan B disebut saling lepas jika jika himpunan A dan B tidak mempunyai anggota persekutuan. Dengan kata lain, setiap anggota himpunan A berbeda dengan setiap anggota himpunan B. Simbol himpunan lepas dinyataka dengan tanda ǁ. Sehingga untuk himpunan A dan B yang saling lepas dinotasikan dengan A ǁ B.
Sebagai contoh himpunan A = {v, w, x, y, z} dan B = {sate, soto, bakso, mie ayam}. Diketahui bahwa himpunan A adalah lima huruf terakihir dalam urutan abjad. Sedangkan B adalah himpunan dengan empat anggota berupa nama-nama makanan.
Antara anggota A dan B tidak memiliki kesamaan sehingga dapat disimpulkan bahwa A dan B merupakan himpunan lepas.
Baca Juga: Beberapa Bentuk Soal Diagram Venn pada TPA/TPS UTBK
Contoh Soal Hubungan Himpunan dengan Himpunan dan Pembahasannya
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman sobat idschool. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Hubungan Himpunan dengan Himpunan
Perhatikan pernyataan berikut!
(1) Jika A ⊂ B maka A ∩ B = A
(2) Jika A ⊃ B maka A ∪ B = B
(3) Jika A ⊂ B dan B ∩ C = ø maka A ∩ C = ø
(4) Jika A ⊂ B dan A ∩ C = ø maka B ∩ C = ø
Dari pernyataan tersebut yang benar adalah ….
A. (1) dan (3)
B. (2) dan (4)
C. (1) dan (4)
D. (4) saja
E. semua benar
Pembahasan:
(1) Jika A⊂B maka A∩B = A → benar
A subset B berarti semua anggota A juga merupakan anggota B. Sehingga irisan (∩) dari A dan B merupakan anggota A.
(2) Jika A⊃B maka A∪B = A → salah
A superset B maka semua anggota B juga merupakan anggota A. Gabungan (∪) himpunan A dan B merupakan anggota A (A∪B = A).
(3) Jika A⊂B dan B∩C = ø maka A∩C = ø → benar
A subset B maka semua anggota A juga merupakan anggota B. Diketahui juga bahwa tidak ada anggota B yang sama dengan anggota C. Sehingga irisan A dan C tidak memiliki anggota yang sama (A∩C = ø).
(4) Jika A⊂B dan A∩C = ø maka B∩C = ø → salah
A subset B maka semua anggota A juga merupakan anggota B. Diketahui juga bahwa tidak ada anggota A dan C yang sama. Namun tidak ada keterangan bahwa himpunan B dan C memiliki anggota yang sama.
Jadi, pernyataan yang benar terdapat pada nomor (1) dan (3).
Jawaban: A
Contoh 2 – Hubungan Himpunan dengan Himpunan
Diketahui dua himpunan P dan Q. Jika P – Q = ø maka pernyataan yang benar adalah ….
A. P ⊃Q
B. P⊂Q
C. Q⊃P
D. Q~P
E.
Pembahasan:
P – Q = ø memiliki tiga kondisi kemungkinan yaitu P = Q dan P ⊃Q atau Q ⊃P. Jadi, pernyataan yang benar adalah P ⊃ Q.
Jawaban: A
Contoh 3 – Hubungan Himpunan dengan Himpunan
Jika M ⊂N dan M ≠ N maka ….
A. M∪N = M
B. M∩N = N
C. (M∪N)⊂M
D. N⊂(M∩N)
E. M∪N = N
Pembahasan:
Hubungan M⊂N menunjukkan bahwa setiap anggota M juga merupakan anggota N. Sehingga dapat disimpulkan bahwa M ∩N = M dan M ∪N = N. Jadi, Jika M ⊂N dan M ≠ N maka M∪N = N.
Jawaban: E
Demikianlah tadi ulasan hubungan himpunan dengan himpunan yang dapat dinyatakan melalui beberapa relasi. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Himpunan Penyelesaian pada Persamaan dan Pertidaksamaan Logaritma