Ada empat bentuk persamaan paraoba hasil dari irisan kerucut yang mewakili 4 bentuk parabola yang berbeda. Bentuk irisan kerucut parabola hampir sangat mirip dengan bentuk kurva pada persamaan kuadrat. Bahkan dapat dikatakan sangat mirip. Meskipun memiliki bentuk yang sangat mirip, namun bentuk persamaan parabola hasil dari irisan kerucut memiliki bentuk yang berbeda.
Persamaan parabola hasil irisan kerucut dibedakan berdasarkan bentuknya apakah parabola terbuka ke atas atau ke bawah, apakah parabola terbuka ke kanan atau ke kiri. Selain itu, bentuk persamaan juga bergantung pada letak puncak parabola, apakah parabola memiliki puncak di O(0, 0) atau terletak di titik lain. Sebelum membahas lebih lanjut tentang persamaan parabola hasil dari irisan kerucut, ingat kembali komponen-komponen yang terdapat pada irisan kerucut parabola seperti yang diberikan di atas.

Baca Juga: Cara Menentukan Persamaan Grafik Fungsi Kuadrat
Perhatikan di mana letak titik puncak, titik fokus dari parabola hasil irisan kerucut yang diberikan. Keterangan-keterangan tersebut akan memberikan kemudahan untuk menentukan persamaan dari suatu parabola hasil irisan kerucut. Selanjutnya sobat idschool dapat mempelajasi bagaimana bentuk umum persamaan parabola dengan berbagai kondisi,
Table of Contents
Bentuk Umum Persamaan
Bentuk parabola menyerupai kurva mulus pada persamaan kuadrat. Bentuk parabola hasil irisan kerucut dapat memiliki bentuk terbuka ke atas atau ke bawah dan parabola dengan bentuk terbuka ke samping kanan atau kiri. Bentuk-bentuk parabola yang berbeda memiliki persamaan-persamaan yang berbeda pula.
Berikut ini adalah bentuk umum persamaan parabola dengan puncak O(0, 0).

Sedangkan untuk bentuk umum persamaan parabola dengan puncak P(a, b) dapat dilihat pada tabel di bawah.

Baca Juga: Persamaan Garis Singgung Parabola
Cara Menggambar Persamaan Parabola
Pembahasan di sini akan mengulas cara menggambar irisan kerucut parabola jika diketahui sebuah bentuk umum persamaan parabola. Bentuk umum persamaan yang diberikan di atas akan menjadi patokan untuk membuat gambar parabola. Misalkan, diberikan sebuah persamaan untuk suatu parabola seperti berikut.
(y – 2)2 = 8(x – 1).
Berdasarkan persamaan di atas, dapat disimpulkan bahwa letak puncak parabola tersebut adalah P(1, 2), nilai p = 2, dan titik fokusnya adalah (3, 2).
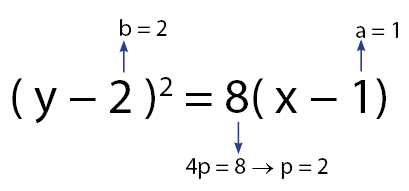
Gambar bentuk parabolan bedasarkan persamaan yang diberikan sesuai dengan ilustrasi berikut.

Bagaimana? Sudah cukup jelas dengan cara menggambar parabola yang diberikan di atas? Berikutnya, akan diulas cara menentukan persamaan parabola dari sebuah gambar parabola yang diketahui. S
Baca Juga: Kedudukan Titik Terhadap Parabola
Cara Menentukan Persamaan Parabola
Dalam beberapa pembahasan, terdapat soal yang menanyakan suatu persamaan jika diketahui sebuah gambar parabola. Cara menentukan rumus parabola tersebut dapat secara mudah ditemukan dengan melihat bagian-bagian yang diketahui pada gambar parabola. Selain itu, sobat idschool juga perlu mengetahui bentuk persamaan umum dari parabola yang telah diberikan pada ulasan di atas.
Soal:
Carilah bentuk persamaan irisan kerucut parabola untuk gambar di bawah!
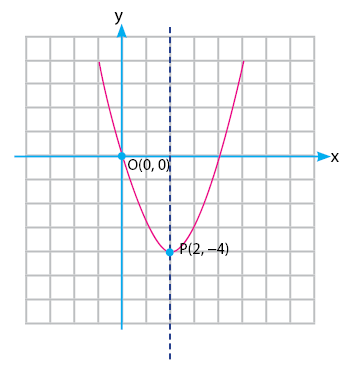
Untuk mendapatkan persamaan parabola, pertama kita cari tahu terlebih dahulu informasi yang dapat diperoleh dari gambar parabola pada soal. Informasi yang dapat diperoleh meliputi titik puncak (2, −4) dan kurva parabola melalui titik O(0, 0).
Bentuk umum persamaan irisan kerucut berupa parobola yang terbuka ke atas: (x – a)2 = 4p(y – b)
Dengan,
a dan b = titik puncak parabola
p = titik fokus parabola
Diketahui bahwa parabola memiliki titik puncak (2, −4) dan melalui titik O(0, 0). Dengan menyesuaikan bentuk persamaan umum dari parabola dapar diperoleh persamaan (x – 2)2 = 4p(y + 4)
Hasil persamaan parabola seperti di atas belum selesai, masih ada variabel p yang harus dicari nilainya. Untuk mendapatkan persamaan parabola yang sempurna, sobat idschool perlu mendapatkan nilai p tersebut.
Menghitung nilai p:
Perhatikan bahwa kurva parabola melalui titik O(0, 0). Substitusi titik O(0, 0) untuk mendapatkan nilai p.
(0 – 2)2 = 4p(0 + 4)
(–2)2 = 4p(4)
4 = 16 p
p =4/16
p = ¼
Diperoleh nilai p = ¼, sehingga persamaan parabola dapat ditentukan seperti pada proses pengerjaan cara substitusi nilai p = ¼ pada persamaan umum parabola sebelumnya.
(x – 2)2 = 4 (¼)(y + 4)
(x – 2)2 = (y + 4)
Demikianlah ulasan tentang persamaan parabola hasil dari irisan kerucut. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Kedudukan Garis Terhadap Parabola
