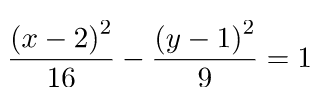Kedudukan Garis Terhadap Hiperbola

Hiperbola merupakan salah satu bentuk dari irisan kerucut. Bentuknya menyerupai kurva persamaan kuadrat dan hasil pencerminannya. Fokus pembahasan pada halaman ini adalah kedudukan garis terhadap hiperbola. Kedudukan garis pada hiperbola memuat tiga kondisi. Ketiga kondisi tersebut meliputi garis tidak memotong hiperbola, garis menyinggung hiperbola, dan garis memotong hiperbola di dua titik.

Gambar ketiga kedudukan garis terhadap hiperbola dapat dilihat pada gambar di bawah.

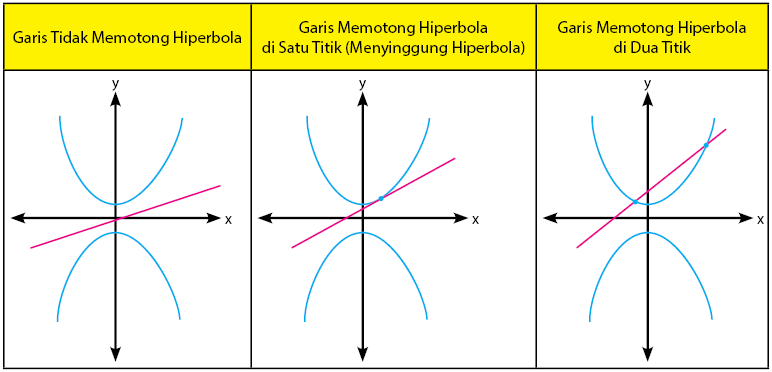
Cara mengetahui kedudukan garis terhadap hiperbola dapat dilakukan melalui gambar. Seperti pada tiga contoh kondisi kedudukan garis terhadap hiperbola di atas. Namun cara tersebut bukan hal yang menguntungkan. Karena pastinya akan membutuhkan sedikit lebih banyak waktu.

Dan tentu ada cara lain yang lebih sederhana, tanpa harus melihat kedudukan garis pada hiperbola melalui gambar.

Cara tersebut diperoleh dengan melihat nilai diskriminan dari persamaan kuadrat, hasil substitusi persamaan garis ke persamaan hiperbola. Untuk itu, sobat idschool perlu mengetahui apa yang dimaksud diskriminan terlebih dahulu.

Table of Contents

• Apa Itu Diskriminan?
• Garis Tidak Memotong Hiperbola
• Garis Memotong Hiperbola di Satu Titik (Menyinggung Hiperbola)
• Garis Memotong Hiperbola di Dua Titik

Apa Itu Diskriminan?

Diskriminan adalah hubungan antara koefisien dalam persamaan kuadrat untuk mencari hubungan kedudukan garis terhadap parabola. Jika diketahui persamaan kuadrat y = ax² + bx + c maka nilai diskriminannya dapat diperoleh melalui rumus D = b² – 4ac.

Setelah mengetahui apa itu diskriminan, berikutnya adalah bagaimana cara menggunakannya. Apa hubungan antara nilai diskriminan dengan kedudukan garis terhadap hiperbola? Untuk mengetahui jawabannya ikuti langkah – langkah berikut.

Langkah-langkah menentukan kedudukan garis terhadap hiperbola:

1. Substitusi persamaan garis lurus ke dalam persamaan hiperbola sehingga diperoleh persamaan kuadrat.
2. Menentukan nilai diskriminan dari hasil persamaan kuadrat yang diperoleh.
3. Menyimpulkan hasilnya, apakah garis tidak memotong hiperbola, garis memotong hiperbola di satu titik, atau garis memotong hiperbola di dua titik.
4. Kesimpulan ini diperoleh dari nilai diskriminan yang telah dihitung pada poin ke dua.

Kriteria kedudukan garis terhadap hiperbola akan dibahas secara lebih lengkap pada pembahasan di bawah. Untuk pembahasan pertama adalah kriteria garis tidak memotong hiperbola. Simak ulasan materinya pada pembahasan di bawah.

Baca Juga: Kedudukan Titik Terhadap Elips

Garis Tidak Memotong Hiperbola

Garis dikatakan tidak memotong hiperbola jika kedudukan garis pada hiperbola tidak memiliki satupun titik potong garis pada hiperbola. Hal ini dipenuhi ketika nilai diskriminan dari persamaan kuadrat hasil substitusi persamaan garis ke persamaan hiperbola memiliki nilai kurang dari nol, D < 0.

Perhatikan gambar dan kriteria garis yang tidak memotong hiperbola seperti pada gambar di bawah.

Untuk menambah pemahaman sobat idschool akan diberikan contoh soal kedudukan garis yang tidak memotong hiperbola.

Contoh soal kedudukan garis terhadap hiperbola untuk garis tidak memotong hiperbola.

Tentukan kedudukan garis y = x – 2 pada hiperbola dengan persamaan berikut.

Pembahasan:
Langkah pertama yang dilakukan adalah substitusi nilai y = x – 2 pada persamaan hiperbola.

Berdasarkan persamaan kuadrat hasil substitusi persamaan garis ke persamaan parabola, diperoleh a = -7, b = 60, dan c = -252. Sehingga, nilai diskriminannya dapat ditentukan seperti cara berikut.

Nilai diskriminan (D):
D = b² – 4ac
D = 60² – 4(-7)(-252)
D = 3.600 – 7.056 = -3.456

Berdasarkan hasil perhitungan diskriminan di atas, dapat disimpulkan bahwa garis tidak memotong hiperbola, karena D < 0.

Untuk membuktikannya, perhatikan gambar di bawah yang merupakan gambar garis dan hiperbola sesuai dengan soal yang diberikan.

Terlihat bahwa garis tidak memotong hiperbola, bukan?

Baca Juga: Kedudukan Titik Terhadap Hiperbola

Garis Memotong Hiperbola di Satu Titik (Menyinggung Hiperbola)

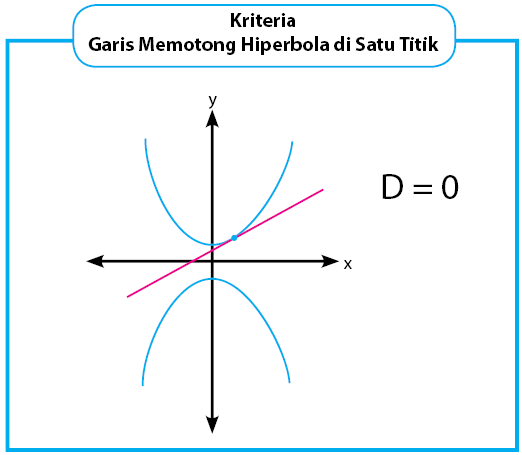
Pembahasan berikutnya adalah kedudukan garis terhadap hiperbola untuk kasus garis memotong hiperbola di satu titik, atau biasa disebut dengan garis menyinggung hiperbola. Kriteria garis memotong hiperbola di satu titik dipenuhi saat nilai determinan sama dengan nol, D = 0.

Perhatikan gambar hiperbola dan garis lurus yang menyinggung di satu titik beserta dengan kriterianya.

Contoh soal kedudukan garis terhadap hiperbola untuk garis memotong hiperbola di satu titik (menyinggung elips).

Tentukan kedudukan garis x = – 2 pada hiperbola dengan persamaan berikut.

Jawab:
Langkah pertama yang dilakukan adalah substitusi nilai x = – 2 pada persamaan hiperbola.

Berdasarkan persamaan kuadrat hasil substitusi persamaan garis ke persamaan parabola, diperoleh a = -1, b = 2, dan c = – 1. Sehingga, nilai diskrimina untuk persamaan hasil substitusi persamaan garis ke persamaan elips dapat ditentukan seperti cara berikut.

Nilai diskriminan (D):
D = b² – 4ac
D = 2²– 4(–1)(–1)
D = 4 – 4 = 0

Berdasarkan hasil perhitungan diskriminan di atas, dapat disimpulkan bahwa garis memotong hiperbola di satu titik, karena D = 0.

Untuk membuktikannya, perhatikan gambar berdasarkan soal yang sama dengan pembahasan di atas.

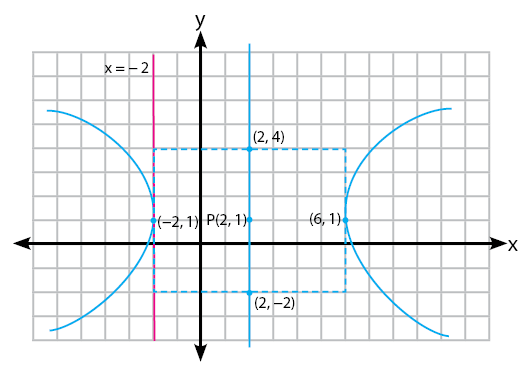
Terlihat bahwa garis menyinggung hiperbola di satu titik, dengan kata lain garis menyinggung hiperbola.

Baca Juga: Irisan Kerucut – Hiperbola

Garis Memotong Hiperbola di Dua Titik

Sebuah garis dikatakan memotong hiperbola di dua titik jika memiliki dua titik yang sama-sama dilalui garis lurus dan hiperbola. Kondisi ini dapat dilihat dari nilai diskriminannya yang lebih dari nol, D > 0. Ilustrasi gambar garis lurus yang memotong hiperbola di dua titik beserta kriterianya dapat dilihat pada gambar di bawah.

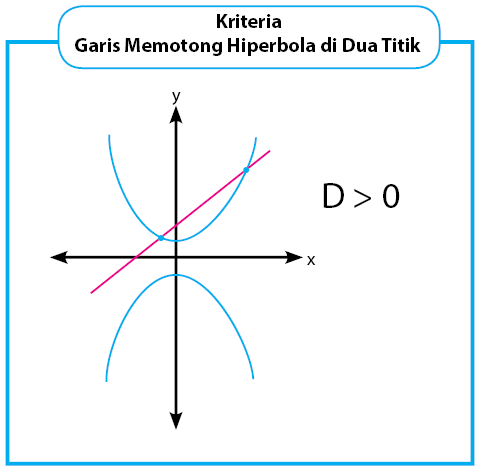
Contoh soal kedudukan garis terhadap hiperbola untuk garis memotong hiperbola di dua titik.

Tentukan kedudukan garis y = x + 3 pada hiperbola dengan persamaan berikut.

Jawab:
Langkah pertama yang dilakukan adalah substitusi nilai y = x + 3 pada persamaan hiperbola.

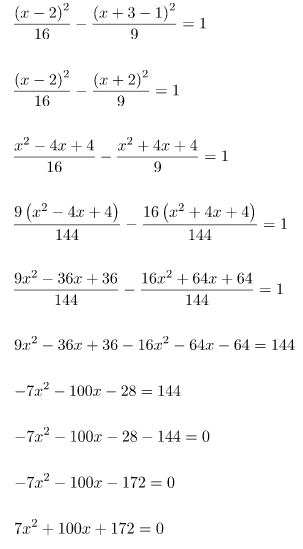
Berdasarkan persamaan kuadrat hasil substitusi persamaan garis ke persamaan parabola, diperoleh a = 7, b = 100, dan c = 172. Selanjutnya, nilai diskriminan hasil substitusi persamaan garis ke persamaan elips dapat ditentukan seperti cara berikut.

Nilai diskriminan (D):
D = b² – 4ac
D = 100² – 4(7)(172)
D = 10.000 – 4.816 = 5.184

Berdasarkan hasil perhitungan diskriminan di atas, dapat disimpulkan bahwa garis memotong parabola di dua titik (karena D > 0). Untuk membuktikannya, perhatikan gambar di bawah.

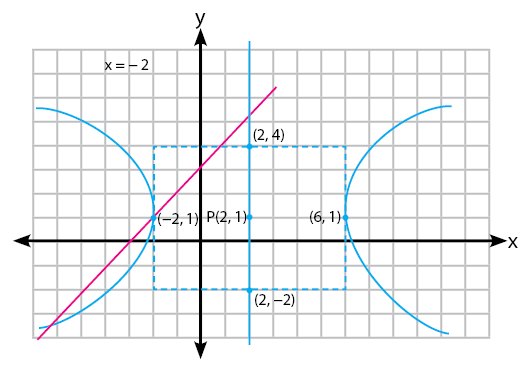
Terlihat bahwa garis memotong hiperbola di dua titik.

Bagaimana ulasan materi yang diberikan? Sudah paham? Mudah bukan? Jika belum paham bisa dipahami sekali lagi pelan-pelan, pasti akan paham. Intinya, ketiga kriteria menentukan kedudukan garis terhadap hiperbola dirangkum dalam tiga syarat dalam tabel di bawah.

Sekian pembahasan kedudukan garis terhadap hiperbola yang meliputi garis tidak memotong hiperbola, garis memotong hiperbola di satu titik (garis menyinggung hiperbola), dan garis memotong hiperbola di dua titik. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Irisan Kerucut (Lingkaran, Elips, Parabola, Hiperbola)