Persamaan garis singgung elips adalah persamaan garis lurus yang memiliki satu titik potong dengan elips. Secara umum persamaan garis lurus memiliki bentuk y = ax + c, sedangkan persamaan elips memiliki beberapa bentuk bergantung dari letak titik pusat dan panjang sumbu mayor/minor. Cara mencari persamaan garis singgung elips terbagi ke dalam dua kondisi. Pertama adalah persamaan garis singgung yang diketahui nilai gradien garis. Kedua adalah persamaan garis singgung yang diketahui melalui sebuah titik.
Sebuah saris singgung pada suatu elips dapat saling sejajar atau tegak lurus dengan garis lain. Contoh kedudukan garis lurus menyinggung elips dengan garis lain yang saling sejajar dan tegak lurus diberikan seperti berikut.

Bentuk umum persamaan garis lurus yang menyinggung elips meliputi 2 macam yaitu ketika diketahui memiliki gradien m atau melalui sebuah titik. Bagaimanakah cara menentukan persamaan garis singgung elips? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Persamaan Garis Singgung Elips dengan Gradien m
- Persamaan Garis Singgung Elips Melalui Suatu Titik
- Contoh Soal dan Pembahasan
Persamaan Garis Singgung Elips dengan Gradien m
Masuk ke pembahasan pertama yaitu persamaan garis lurus yang menyinggung elips dengan keterangan memiliki nilai gradien m. Cara mencari garis singgung elips yang memiliki nilai gradien m memiliki beberapa bentuk persamaan umum bergantung dari persamaan elips. Kondisi ini dikarenakan elips memiliki beberapa bentuk persamaan umum yang bergantung dari letak titik pusat dan panjang sumbu mayor/minor.
Cara mencari garis singgung pada elips dengan pusat O(0, 0) tentu akan berbeda dengan garis singgung pada elips dengan pusat (p, q). Meskipun demikian, konsep yang digunakan untuk mencari garis singgung elips tersebut adalah sama, bentuk rumusnya juga mirip sehingga mudah untuk dihafal (dipahami).
Berikut ini adalah kumpulan rumus yang digunakan untuk mencari persamaan garis singgung dengan gradien m yang menyinggung elips.

Contoh peggunaan rumus umum persamaan garis singgung elips dapat dilihat pada akhir bagian (pada bagian contoh soal dan pembahasan).
Baca Juga: Kedudukan Titik Terhadap Elips
Persamaan Garis Singgung Elips Melalui Suatu Titik
Cara mencari persamaan garis singgung pada elips yang melalui suatu titik dibedakan kedalam lima persamaan. Cara menggunakan persamaan garis singgung tersebut tergantung dari bentuk persamaan elips yang diberikan pada soal. Kumpulan rumus yang digunakan untuk mencari persamaan garis yang melalui titik (x1, y1) dan menyinggung suatu elips dapat dilihat pada tabel di bawah.

Baca Juga: Persamaan Elips Hasil dari Irisan Kerucut
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1: Soal Persamaan Garis Singgung Elips
Persamaan garis singgung elips dengan persamaan x2 + 4y2 = 4 dan sejajar dengan garis y = x + 3 adalah ….
A. y = x + 25
B. y = x + √5
C. y = x + 1
D. y = x – 5
E. y = x + 5
Pembahasan:
Persamaan elips x2 + 4y2 = 4 dapat juga ditulis seperti persamaan di bawah (bagi kedua ruas dengan 4).
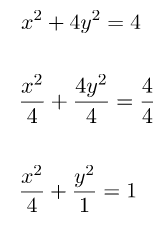
Selanjutnya akan dicari persamaan garis singgung elips dengan persamaan di atas yang sejajar dengan garis y = x + 3. Gradien garis y = x + 3 adalah m = 1, jika belum paham cara mencari gradien dapat dilihat di sini. Selanjutnya, kita akan menggunakan rumus persamaan garis singgung elips dengan gradien m untuk menentukan persamaan garis singgungnya.
Gradien garis yang akan dicari nilainya adalah m = 1, karena garis yang akan dicari sejajar dengan y = x + 3. Berdasarkan persamaan elips, diperoleh informasi bahwa a = 2 dan b = 1.
Sehingga, persamaan garis singgung elips yang sejajar dengan y = x + 3 dapat dicari seperti pada cara berikut.

Jadi, diperoleh persamaan garis singgungnya adalah y = x + √5 atau y = x – √5.
Jawaban: B
Baca Juga: 4 Cara Menentukan Gradien
Contoh 2: Soal Persamaan Garis Singgung Elips
Diberikan persamaan elips:

Persamaan garis singgung yang melalui titik (9, 4) dan menyinggung elips tersebut adalah ….
A. x + y = 13
B x + y = 13
C. x + y = 13
D. x + y = 13
E. x + y = 13
Pembahasan:
Persamaan garis yang menyinggung elips dengan pusat (p, q) dan melalui titik (x1, y1) secara umum memiliki persamaan berikut.
Diketahui bahwa garis singgung melalui titik (9, 4), sehingga persamaan garis singgung elips pada soal yang diberikan dapat ditentukan seperti cara berikut.

Jawaban: A
Sekian pembahasan materi persamaan garis singgung elips yang meliputi bentuk keterangan gradien m dan melalui suati titik. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Kedudukan Titik Terhadap Elips

