Kumpulan Soal Limit Fungsi Trigonometri

Halaman ini berisi kumpulan soal limit fungsi trigonometri yang sudah dilengkapi dengan pembahasannya. Teknik mengerjakan soal limit fungsi trigonometri berbeda untuk setiap soalnya. Masing-masing tipe soal mempunyai cara tertentu untuk mengerjakan. Meskipun berbeda teknik, namun tidak banyak teknik yang perlu dikuasai.

Satu pemahaman konsep teknik mengerjakan dapat digunakan untuk mengerjakan berbagai macam soal dengan tipe sejenis. Selain itu, sobat idschool juga perlu memahami (sampai hafal jika perlu) rumus sudut rangkap fungsi trigonometri. Rumus tersebut dapat digunakan bersama-sama rumus identitas trigonometri lainnya untuk membantu memecahkan soal limit trigonometri.

Selanjutnya, simak kumpulan soal limit fungsi trigonometri berbagai jenis berikut ini.

Table of Contents

• Contoh 1 – Soal Limit Fungsi Trigonometri
• Contoh 2 – Limit Fungsi Trigonometri
• Contoh 3 – Soal Limit Fungsi Trigonometri
• Contoh 4 – Soal Limit Fungsi Trigonometri
• Contoh 5 – Soal Limit Fungsi Trigonometri
• Contoh 6 – Soal Limit Fungsi Trigonometri
• Contoh 7 – Soal Limit Fungsi Trigonometri
• Contoh 8 – Soal Limit Fungsi Trigonometri (UMPTN Tahun 2001)
• Contoh 9 – Soal Limit Fungsi Trigonometri
• Contoh 10 – Soal Limit Fungsi Trigonometri
• Contoh 11 – Soal Limit Fungsi Trigonometri

Contoh 1 – Soal Limit Fungsi Trigonometri

Nilai dari limit fungsi di bawah adalah ….
A. 6
B. 5
C. 4
D. 2
E. 0

Pembahasan:
Pertama, kita akan coba kerjakan menggunakan substitusi seperti yang dijelaskan pada cara tips mengerjakan limit.

Hasil akhir yang diperoleh bukan merupakan jawaban yang diharapkan, sehingga kita perlu mencari nilai limit yang tepat. Selanjutnya, gunakan metode pemfaktoran.

Jawaban: C

Contoh 2 – Limit Fungsi Trigonometri

Pembahasan:
Penyelesaian dari nilai limit pada persamaan di atas dapat diselesaikan dengan cara berikut.

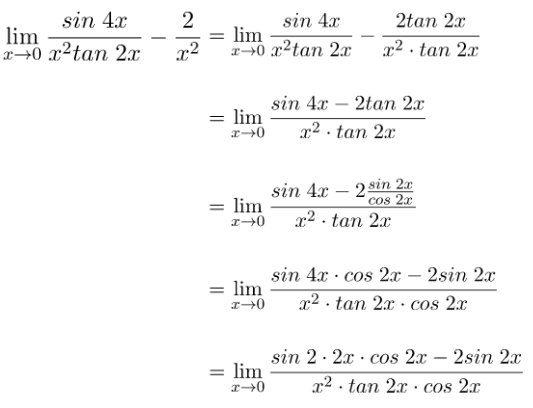
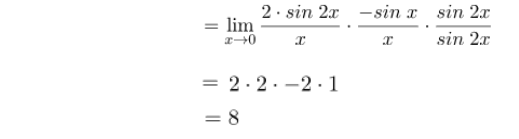
Jadi, nilai limit dari persamaan fungsi yang diberikan adalah 8.
Jawaban: B

Contoh 3 – Soal Limit Fungsi Trigonometri

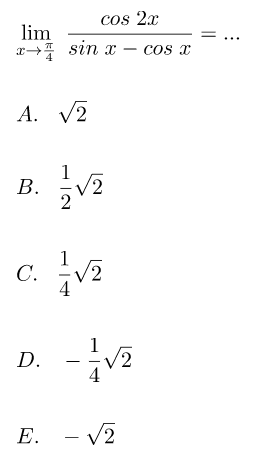
Pembahasan:
Soal yang diberikan pada soal dikerjakan dengan kombinasi pemfaktoran dan memanipulasi dengan identitas trigonometri. Identitas trigonometri yang digunakan adalah cosinus sudut rangkap yaitu cos 2x = cos²x – sin²x.

Sekarang perhatikan proses pengerjaannya seperti yang dilakukan pada cara berikut.

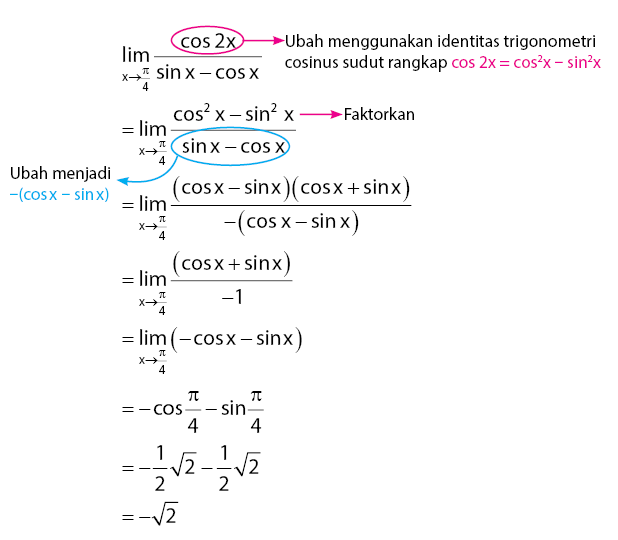
Jawaban: E

Baca Juga: Pengertian Limit

Contoh 4 – Soal Limit Fungsi Trigonometri

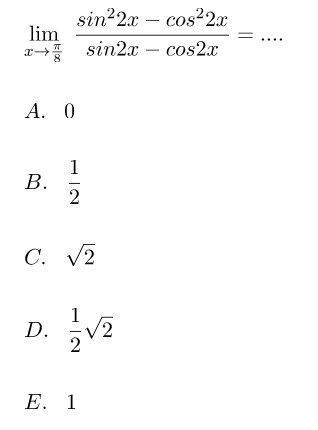
Pembahasan:
Nilai limit fungsi yang diberikan pada soal dapat dicari seperti pengerjaan pada cara berikut.

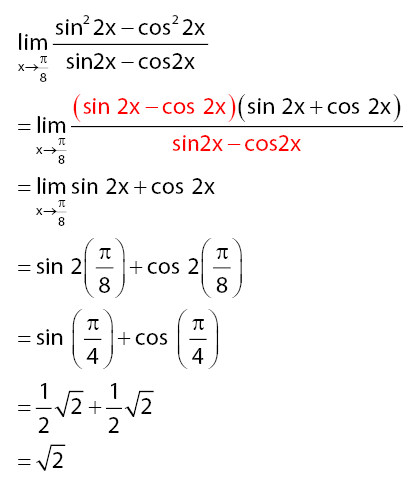
Jawaban: C

Contoh 5 – Soal Limit Fungsi Trigonometri

Pembahasan:
Misalkan: p = x – 2, maka nilai limit fungsi pada soal yang diberikan di atas dapat diselesaikan melalui cara berikut.

Jawaban: E

Baca Juga: Cara Menentukan Nilai Limit Mendekati Tak Hingga dari Suatu Fungsi

Contoh 6 – Soal Limit Fungsi Trigonometri

Nilai limit fungsi dari persamaan di atas adalah ….
A. -2
B. -1
C. 0
D. 1
E. 2

Pembahasan:
Ingat kembali identitas trigonometri dari cosinus sudut rangkap: 1 – cos 2x = 2 sin²x
Nilai limit pada soal dapat diperoleh dengan melakukan transformasi menggunakan identitas trigonometri terlebih dahulu, seperti yang dilakukan pada cara berikut.

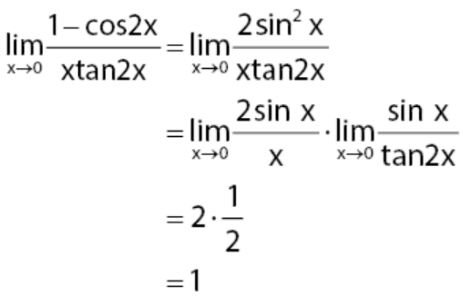
Jadi, nilai limit fungsi dari persamaan di atas adalah 2.

Jawaban: E

Contoh 7 – Soal Limit Fungsi Trigonometri

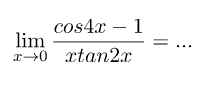
Nilai limit fungsi dari persamaan di atas adalah ….
A. 4
B. 2
C. ‒1
D. ‒2
E. ‒4

Pembahasan:
Perhatikan bahwa: cos 4x – 1= cos 2(2x) – 1 = – 2sin²2x, nilai limit fungsi pada soal yang diberikan dapat dilakukan seperti pada cara pengerjaan berikut.

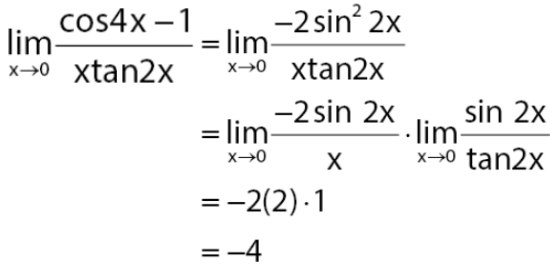
Jadi, nilai limit fungsi dari persamaan di atas adalah ‒4.

Jawaban: E

Baca Juga: Rumus Cepat pada Limit Tak Hingga

Contoh 8 – Soal Limit Fungsi Trigonometri (UMPTN Tahun 2001)

Nilai limit fungsi dari persamaan di atas adalah ….
A. ¹/₂
B. ¹/₃
C. ¹/₆
D. ¹/₁₂
E. ¹/₁₈

Pembahasan:
Nilai limit fungsi dari persamaan yang diberikan pada soal dapat ditentukan seperti pada cara berikut.

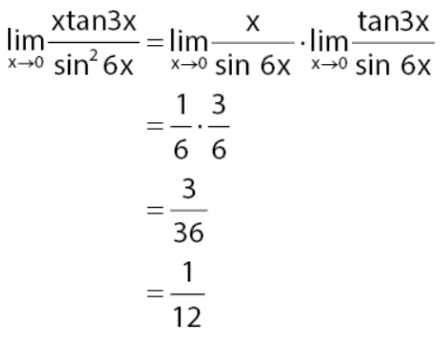
Jadi, nilai limit fungsi dari persamaan di atas adalah ¹/₁₂.

Jawaban: D

Contoh 9 – Soal Limit Fungsi Trigonometri

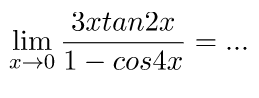
Nilai limit fungsi di atas adalah ….
A. ¹/₈
B. ³/₈
C. ¹/₄
D. ³/₄
E. 1¹/₄

Pembahasan:
Ingat kembali identitas trigonometri: 1 – cos 4x = 1 – cos 2(2x) = 2 sin²2x, nilai limit fungsi pada soal yang diberikan dapat dikerajakan seperti pada penyelesaian cara berikut.

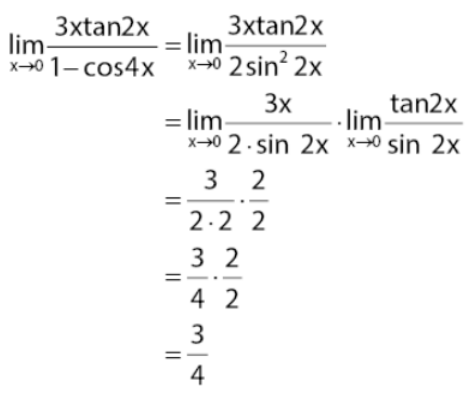
Jadi, nilai limit fungsi dari soal yang diberikan adalah ¹/₈.

Jawaban: D

Baca Juga: Limit Fungsi Trigonometri

Contoh 10 – Soal Limit Fungsi Trigonometri

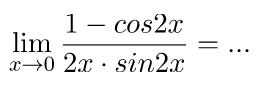
Nilai limit fungsi di atas adalah ….
A. ‒²/₃
B. ‒¹/₃
C. ¹/₂
D. ²/₃
E. 1

Pembahasan:
Identitas trigonometri 1 ‒ cos 2x = 2sin²x
Dengan menggunakan identitas trigonometri tersebut, nilai limit fungsi dari soal yang diberikan dapat dicari seperti pada cara pengerjaan berikut.

Jadi, nilai limit fungsi dari soal yang diberikan adalah ¹/₂.

Jawaban: C

Contoh 11 – Soal Limit Fungsi Trigonometri

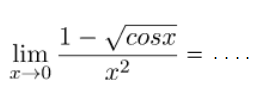
Nilai limit fungsi di atas adalah ….
A. ¹/₈
B. ³/₈
C. ¹/₄
D. ³/₄
E. 1¹/₄

Pembahasan:
Teknik pengerjaan yang digunakan untuk menyelesaikan soal nilai limit seperti pada soal yang diberikan adalah dengan mengalikan akar sekawan. Perhatikan proses pengerjaan seperti yang ditunjukkan pada cara berikut.

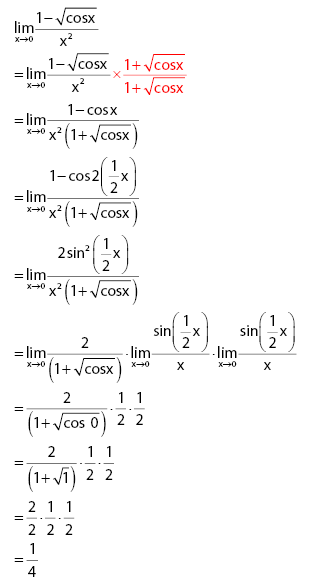
Jawaban: C

Sekian kumpulan soal limit fungsi trigonometri disertai dengan pembahasannya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Kumpulan Identitas Trigonometri