Jarak Titik ke Bidang pada Dimensi Tiga (R3)

Jarak titik ke bidang sama dengan panjang ruas garis terpendek yang menghubungkan titik dengan sebuah titik pada bidang. Di mana titik pada bidang merupakan titik hasil proyeksi dari titik di luar bidang tadi. Sebagai contoh, jarak titik ke A pada bidang α adalah panjang ruas garis AP. Di mana P adalah proyeksi titik A pada bidang α.

Cara menghitung jarak titik ke bidang dapat menggunakan kosep kesebangunan segitiga, teorema Pythagoras, atau perbandingan luas segitiga. Bagaimana cara menghitung jarak titik ke bidang? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Baca Juga: Pasangan Garis Sejajar, Bersilangan, dan Berpotongan pada Kubus ABCD.EFGH

Jarak Titik ke Bidang

Langkah pertama yang harus dilakukan untuk mencari jarak titik ke bidang adalah menentukan ruas garis yang mewakili jarak titik ke bidang. Ruas garis tersebut diperoleh dengan menghubungkan titik dengan proyeksi titik tersebut pada bidang.

Hasil menghubungkan titik dengan titik proyeksi pada bidang adalah sebuah ruas garis. Di mana ruas garis tersebut akan tegak lurus dengan bidang. Ruas garis tersebut merupakan jarak titik ke bidang yang perlu dihitung.

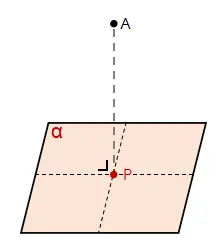
Misal, diketahui sebuah titik A dan bidang α. Titik A tidak terletak pada bidang α (titik A terletak di luar bidang). Proyeksi titik A pada bidang α adalah titik P. Jarak titik ke bidang sama dengan panjang ruas garis AP.

Baca Juga: Apa saja rumus yang digunakan untuk menyelesaikan soal dimensi tiga?

Cara Menentukan Jarak Titik pada Bidang

Jarak titik pada bidang memiliki banyak cara penyelesaian karena banyak sekali ruas garis yang bisa terbentuk, bergantung dari soalnya. Meski begitu, satu hal yang penting untuk selau diperhatikan adalah menentukan mana ruas garis yang perlu dihitung sebagai jarak titik ke bidang.

Langkah menentukan ruas garis yang menjadi jarak titik ke bidang:

• Proyeksikan titik di luar bidang pada bidang
• Hubungkan titik di luar bidang dengan titik proyeksinya
• Diperoleh ruas garis yang menjadi jarak titik ke bidang

Untuk melihat bagaimana cara menentukan manakah ruas garis yang menjadi jarak titik ke bidang, perhatikan penyelesaian contoh-contoh soal berikut.

Soal #1:
Diketahui kubus ABCD.EFGH seperti gambar berikut!

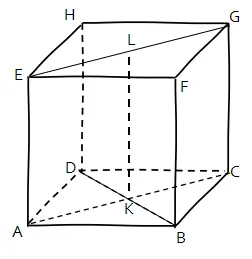
Jarak titik B ke bidang ACGE dapat dinyatakan sebagai panjang ruas garis ….

Jawab:
Proyeksi titik B ke bidang ACGE adalah titik K. Ruas garis yang menghubungkan titik B dan titik K adalah BK. Jadi, panjang ruas garis yang menyatakan jarak titik B ke bidang ACGE adalah BK.

Baca Juga: Jarak Garis ke Garis pada Kubus ABCD.EFGH

Soal #2:
Sebuah balok ABCD.EFGH mempunya rusuk AB, BF, dan BD masing-masing 4 cm, 3 cm, dan 2 cm. Tentukan jarak antara titik A pada bidang BDGF!

Jawab:
Proyeksi titik A pada bidang BCGF adalah titik B. Sehingga, jarak titik A ke bidang BCGF sama dengan panjang ruas garis AB.

Panjang ruas garis AB sama dengan panjang rusuk yaitu AB = 4 cm. Jadi, jarak antara titik A pada bidang BDGF adalah 4 cm.

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan sudah dilengkapi dengan pembahasannya.

Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!

Contoh 1 – Soal Jarak Titik ke Bidang

Sebuah kubus ABCD.EFGH mempunyai panjang rusuk 6 cm, maka jarak titik D terhadap bidang ACH adalah ….
A. 2 cm
B. 2√3 cm
C. 3 cm
D. 3√3 cm
E. 4√3 cm

Pembahasan:
Misalkan proyeksi titik D pada bidang ACH adalah titik P. Jarak titik D terhadap bidang ACH sama dengan panjang ruas garis DP.

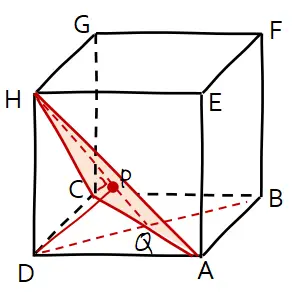
Sebelum menghitung DP, perlu untuk mengetahui panjang beberapa ruas garis lain terlebih dahulu. Beberapa ruas garis yang perlu dihitung terlebih dahulu adalah DQ dan HQ.

Dari gambar dapat diketahui bahwa Q adalah titik potong diagonal bidang. Sehingga panjang DQ sama dengan setengah diagonal bidang kubus.

1) Menghitung panjang ruas garis DQ:
DQ = ¹/₂ × rusuk√2
DQ = ¹/₂ × 6√2 = 3√2 cm

Sementara untuk menghitung HQ dapat menggunakan Teorema Pythagoras dari segitiga siku-siku HDQ. Cara menghitung HQ terdapat pada langkah penyelesaian berikut.

2) Menghitung panjang ruas garis HQ:
HQ² = DH² + DQ² = 6² + (3√2)²
HQ² = 36 + 18 = 54
HQ = √54 = √(9×6) = 3√6 cm

Untuk langkah selanjutnya perhatikan segitiga HDQ. Segitiga tersebut dapat dipandang dengan dua cara. Pertama untuk segitiga dengan alas HQ dan tinggi DP. Kedua adalah segitiga dengan alas DQ dan tinggi HD.

Berdasarkan luas segitiga HDQ akan diperoleh persamaan: ¹/₂ × HQ × DP = ¹/₂ × DQ × DH. Persamaan tersebut dapat digunakan untuk mencari panjang DP seperti pada cara berikut.

3) Menghitubg panjang DP:
¹/₂ × 3√6 × DP = ¹/₂ × 3√2 × 6
3√6 × DP = 18√2

Persamaan di atas dapat dijadikan ke dalam bentuk yang paling sederhana. Cara menjadikan bentuk paling sederhana adalah dengan merasional bentuk akar (mengalikan penyebut dengan akar sekawannya).

4) Menyederhanakan nilai DP:

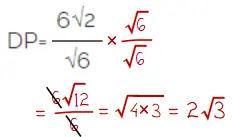
Jadi, jarak D ke bidang ACH sama dengan DP = 2√3 cm.

Jawaban: B

Contoh 2 – Soal Jarak titik ke bidang

Kubus ABCD.EFGH mempunyai panjang rusuk 12 cm. Titik P terletak di tengah diagonal EG. Jarak antara titik P dan bidang BDG adalah ….
A. 8√3 cm
B. 8√2 cm
C. 6√3 cm
D. 6√2 cm
E. 4√3 cm

Pembahasan:
Misalkan proyeksi titik P pada bidang BDG adalah titik Q. Jarak titik P dan bidang BDG sama dengan panjang ruas garis PQ pada gambar di bawah.

Panjang PO sama dengan panjang rusuk kubus karena menghubungkan titik pada alas dan tutup kubus. Sehingga panjang ruas garis PO = rusuk kubus = 12 cm.

Garis PG sama dengan setengah diagonal bidang kubus. Pada kubus, panjang diagonal bidang akan selalu sama dengan panjang rusuk√2. Sehingga panjang ruas garis PG = ¹/₂ × 12√2 = 6√2 cm.

Panjang ruas garis PQ dapat dihitung dari perbandingan segitiga GPO untuk alas PG dan tinggi PO dengan segitiga GPO untuk alas GO dan tinggi PQ.

Panjang PG dan PO sudah diketahui, namun panjang GO belum diketahui. Sehingga panjang GO perlu dihitung terlebih dahulu sebelum menghitung panjang PQ.

Dari segitiga segitiga siku-siku GPO, panjang ruas garis GO dapat dihitung dengan teromema Pythagoras seperti cara berikut.

1) Menghitung panjang garis GO:
GO² = PG² + PO² = (6√2)² + 12²
GO² = 72 + 144 = 216
GO = √(36×6) = √36 × √6 = 6√6 cm

Selanjutnya, panjang PG = 6√2 cm, PO = 12 cm, dan GO = 6√6 cm digunakan untuk menghitung panjang ruas garis PQ seperti langkah penyelesaian berikut.

2) Menghitung panjang garis PQ:
¹/₂ × GO × PQ = ¹/₂ × PG × PO
¹/₂ × 6√6 × PQ = ¹/₂ × 6√2 × 12
6√6 × PQ = 6√2 × 12

PQ = 2√12 = 2√(4×3)
PQ = 2 × √4 × √3
PQ = 4√3 cm

Jadi, jarak antara titik P dan bidang BDG adalah PQ = 4√3 cm.

Jawaban: E

Sekian ulasan cara menghitung jarak titik ke bidang. Di mana jarak titik ke bidang sama dengan panjag ruas garis terpendek yang menghubungkan titik dan bidang. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Dimensi Tiga: Jarak Garis ke Garis