Materi dimensi tiga kelas 12 dimulai dengan memahami pengertian titik, garis, dan bidang. Selanjutnya materi dimensi tiga akan masuk ke bahasan bagaiaman kedudukan titik, garis, bidang, dan antaranya. Setelah itu materi dimensi tiga kelas 12 akan masuk pada jarak dan besar sudut.
Rumus yang digunakan dalam dimensi tiga kelas 12 untuk menghitung jarak dapat menggunakan Teorema Pythagoras, aturan sinus/cosinus, atau fungsi trigonometri. Tidak ada rumus khusus untuk menyelesaikan soal jarak atau besar sudut pada dimensi tiga.
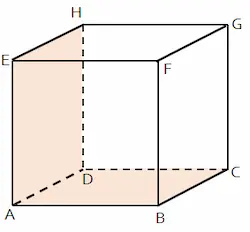
Bahasan dalam dimensi tiga berupa bangun ruang yaitu benda yang memiliki ukuran panjang, lebar, dan tinggi. Bentuk bangun ruang beraturan yang termasuk dalam materi dimensi tiga kelas 12 adalah kubus, balok, prisma, limas, dan lain sebagainya.
Materi dimensi tiga kelas 12 terasa sangat banyak dan rumit, namun sebenarnya tidak demikian. Hanya ada beberapa materi dimensi tiga kelas 12 yang wajib kamu tahu agar bisa menyelesaikan soal dimensi tiga kelas 12 dengan baik. Bahasan materi dimensi tiga kelas 12 yang penting untuk diketahui terdapat pada ulasan di bawah.
Daftar isi:
Baca Juga: Pasangan Garis Saling Sejajar, Bersilangan, dan Berpotongan pada Kubu ABCD EFGH
Pengertian Titik, Garis, dan Bidang
Dimensi tiga adalah benda yang memiliki ukuran panjang, lebar, dan tinggi. Komponen penyusun bangun dengan dimensi tiga adalah titik, garis, dan bidang.

Pengertian titik, garis, dan bidang:
- Titik: obyek yang tidak memiliki besaran dan dimensi, berupa tanda noktah yang diberi nama dengan huruf kapital.
- Garis: himpunan titik-titik yang hanya memiliki ukuran panjang (berdimensi satu)
- Bidang: himpunan titik-titik yang memiliki ukuran panjang dan lebar (berdimensi dua)
Contoh benda dengan dimensi tiga adalah kubus. Bangun ruang berbentu kubus memiliki 8 titik sudut, 12 rusuk berupa garis lurus, dan 6 bidang sisi berupa persegi.
Kedudukan Titik, Garis, dan Bidang pada Dimensi Tiga
Sebuah bangun berupa dimensi tiga memiliki titik, garis, dan bidang. Bagaimana kedudukan titik, garis, dan bidang pada materi dimensi tiga kelas 12 terdapat pada penjelasan berikut.
A) Kedudukan titik terhadap titik, garis, dan bidang
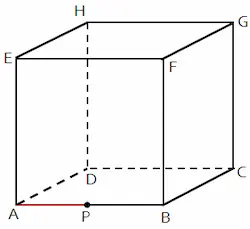
Dua buah titik dapat berimpit atau berkedudukan terpisah. Sebuah titik yang berimpit berada pada satu kedudukan, sementara titik yang terpisah memiliki letak kedudukan yang berbeda.
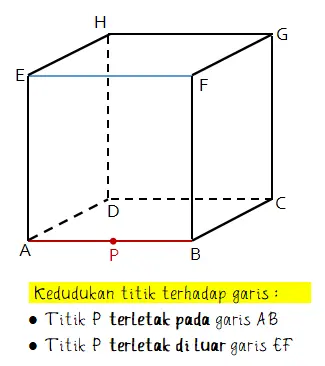
Misalkan titik A dan titik P terletak berimpit. Sedangkan titik B terletak terpisah dari titik A dan P. Kedudukan titik A, B, dan P sesuai seperti gambar berikut.
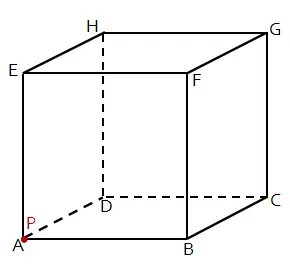
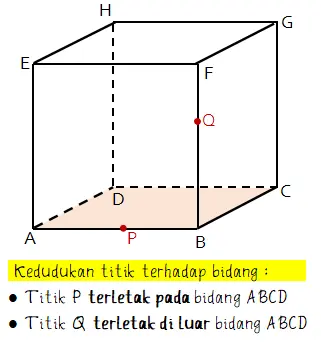
Untuk kedudukan titik terhadap garis dapat terletak pada garis atau terletak di luar garis. Begitu juga dengan kedudukan titik terhadap bidang. Sebuah titik dapat terletak pada bidang atau di luar bidang.
B) Kedudukan garis terhadap garis dan bidang
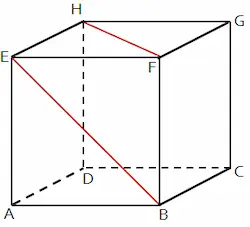
Sebuah bangun yang termasuk dimensi tiga memiliki beberapa ruas garis. Kedudukan garis terhadap garis dan bidang meliputi berpotongan, sejajar, berimpit, dan bersilangan. Keterangan empat kedudukan garis terhadap garis terdapat pada masing-masing penjelasan berikut.
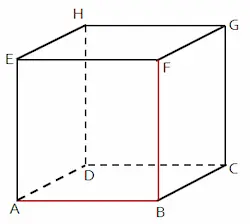
- Berpotongan: kedua garis terletak pada satu bidang dan memiliki satu titik persekutuan (titik potong).
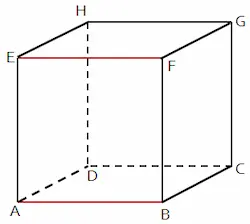
- Sejajar: kedua garis terletak pada satu bidang dan tidak memiliki titik persekutuan (titik potong).
- Berimpit: kedua garis terletak pada satu bidang dan memiliki lebih dari satu titik persekutuan.
- Bersilangan: kedua garis terletak pada bidang yang berbeda dan tidak memiliki titik persekutuan.
Bentuk empat kedudukan garis terhadap garis terdapat pada gambar berikut.
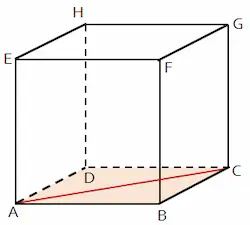
Untuk kedudukan garis terhadap bidang terdiri dari tiga macam. Ketiga kedudukan garis terhadap bidang meliputi sejajar bidang (sejajar), terletak pada bidang (berimpit), memotong bidang (berpotongan).
Penjelasan tiga kedudukan garis terhadap bidang terdapat pada masing-masing penjelasan berikut.
- Sejajar: apabila garis dan bidang tidak memiliki titik persekutuan.
- Berimpit: apabila garis memiliki lebih dari satu titik persekutuan pada bidang.
- Berpotongan: apabila garis memiliki sati titik persekutuan pada bidang.
C) Kedudukan bidang terhadap bidang
Bidang adalah luasan yang hanya dapat dibentuk melalui tiga kondisi yaitu setidaknya dibentuk oleh tiga titik berbeda, satu titik dan satu garis, atau dua garis yang berpotongan/sejajar.
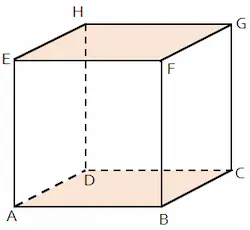
Kedudukan antara bidang dan bidang atau kedudukan antara dua bidang terdiri dari tiga macam. Tiga kedudukan antara dua bidang meliputi berimpit, sejajar, dan berpotongan.
Penjelasan tiga kedudukan antara dua bidang terdapat pada masing-masing penjelasan berikut.
- Sejajar: dua bidang dikatakan sejajar jika kedua bidang tersebut tidak bersekutu pada satu titik manapun.
- Berimpit: dua bidang dikatakan berimpit jika kedua bidang tersebut saling bersekutu.
- Berpotongan: dua bidang dikatakan berpotongan jika kedua bidang itu mempunyai sebuah garis persekutuan atau garis perpotongan.
Baca Juga: Jarak 2 Garis Bersilangan pada Kubus ABCD EFGH
Rumus Jarak dan Besar Sudut pada Materi Dimensi Tiga Kelas 12
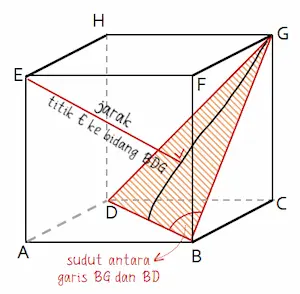
Dalam materi dimensi tiga kelas 12 akan banyak berhubungan dengan cara menjari jarak dan besar sudut. Tidak ada rumus khusus untuk dimensi tiga kelas 12. Panjang jarak dan besar sudut pada materi dimensi tiga kelas 12 dihitung dengan beberapa rumus dari materi lain.
Rumus dimensi tiga yang cukup sering digunakan adalah Teorema Pythagoras dan fungsi trigonometri. Kedua rumus tersebut digunakan saat perhitungan yang dilakukan melibatkan segitiga siku-siku.
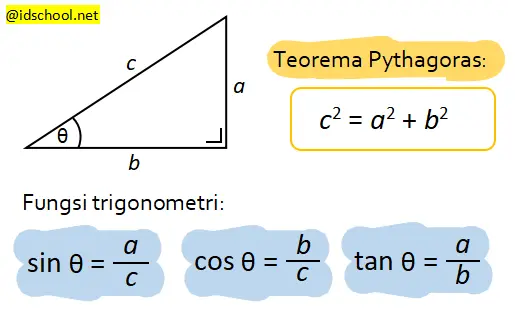
Untuk perhitungan pada bentuk bukan segitiga siku-siku, penyelesaian soal dimensi tiga dapat menggunakan aturan sinus atau aturan cosinus.
Bagaimana penerapan mareri dan penggunaan rumus dimensi tiga kelas 12 terdapat pada halaman pembahasan kumpulan contoh soal soal dimensi tiga.
Baca Juga:
- 1) Jarak titik ke titik, 2) Jarak titik ke garis, 3) Jarak titik ke bidang
- 4) Jarak garis ke garis, 5) Jarak garis ke bidang
- 6) Jarak bidang ke bidang
Sekian pembahasan materi dimensi tiga kelas 12 Matematika SMA. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!