Notasi faktorial merupakan notasi operasi hitung yang disimbolkan dengan tanda seru (!). Notasi ini menandakan bahwa perhitungan yang harus dilakukan adalah mengalikan semua bilangan asli dari bilangan paling besarnya sampai dengan bilangan satu. Di mana bilangan paling besar adalah bilangan yang berada di depan simbol faktorial. Misalnya pada notasi 3! dapat dihitung dengan cara mengalikan semua asli dari 3 sampai 1 yaitu 3 × 2 × 1 = 6. Contoh lain, pada notasi 12! = 12 × 11 × 10 × … × 3 × 2 × 1.
Notasi faktorial secara umum dinyatakan dengan simbol n! di mana n merupakan bilangan cacah. Bilangan cacah adalah himpunan ilangan yang dimulai dari o sampai tak hingga banyaknya. Secara matematis, himpunan bilangan cacah memenuhi C = 0, 1, 2, 3, 4, dan seterusnya. Bilangan bulat negatif tidak memiliki definisi nilai faktorial karena nilainya yang mengecil secara terus menerus sampai bilangan negatif tak hingga.
Baca Juga: Pengertian/Perbedaan Permutasi dan kombinasi
Bagaimana bentuk u? mudah bukan, cara menghitung operasi hitung pada notasi faktorial. Sekarang kita lanjut ke pembahasan definisi umum untuk notasi faktorial. Untuk setiap n bilangan asli, maka berlaku persamaan notasi faktorial di bawah.
Table of Contents
Rumus Umum Notasi Faktorial
Pada aturan perkalian terdapat operasi yang perkalian kejadian-kejadian berlainan. Di mana jika suatu kejadian dapat terjadi dalam n1 cara yang berlainan dan kejadian yang lain dapat terjadi dalam n2 cara yang berlainan. Kejadian-kejadian tersebut secara bersama dapat terjadi dalam n1 × n2 cara yang berlainan. Penyimbolan untuk perkalian bilangan-bilangan cacah tersebut dinyatakan dalam notasi faktorial.
Secara umum, rumus notasi faktorial dinyatakan dengan persamaan n! = n × (n‒1) × (n‒1) × … × 3 × 2 × 1.
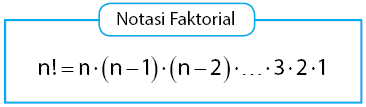
Beberapa contoh opersai hitung untuk menentukan nilai faktorial suatu bilangan terdapat seperti pada persamaan di bawah.
- 5! = 5 × 4 × 3 × 2 × 1
5! = 120 - 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1
7! = 5.040 - 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
10! = 3.628.800 - (n+1)! = (n+1) × n!
- (n+2)! = (n+2) × (n+1) ×n!
- (n-2)! = (n-2) × (n-3) × (n-4)!
Baca Juga: Peluang Suatu Kejadian
Mengapa 1! = 1 dan 0! = 1
Suatu operasi hitung biasanya tidak akan memiliki nilai yang sama. Misalnya pada perkalian, hasil dari 0 dikali 1 tidak akan sama dengan 1 dikali 1. Hasil 0 × 1 = 0 dan 1 × 1 = 1. Atau dalam pembagian, hasil 0 dibagi 1 tidak akan sama dengan 1 di bagi 1. Hasil 0/1 = 0 dan 1/1 = 1.
Namun, ada dua bilangan yang memiliki hasil nilai faktorial yang sama yaitu 1! sama dengan 0!. Kedua hasil faktorial dari kedua bilangan tersebut adalah 1. Mengapa?

Penjelasan:
Jika nilai n = 1, maka akan diperoleh persamaan: 1! = 1 × 0!, selanjutnya diteruskan pada cara di bawah.
1! = 1 × 0!
0! = 1!/1
0! = 1!
0! = 1
Jadi, terbuktilah bahwa nilai dari 0! = 1 sama dengan 1! = 1.
Baca Juga: Aturan Pengisian Tempat (Filling Slot)
Contoh Soal Notasi Faktorial dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Cara Menyatakan Notasi Faktorial
Notasi faktorial untuk persamaan (n+2) × (n+1) × n × (n-1) adalah ….
A. (n – 2)!/n!
B. (n + 2)!/(n-2)!
C. (n – 2)!/(n+2)!
D. n!/(n+2)!
E. n!/(n-2)!
Pembahasan:
Secara umum, notasi faktorial dinyatakan dalam persamaan n! = 1×2×3×…×n atau dapat juga dinyatakan dengan n! = n×(n-1)×(n-2)×…×3×2×1. Notasi faktorial untuk persamaan (n+2) × (n+1) × n × (n-1) dapat diperoleh dengan cara mengalikan (n – 2)!/(n-2)! seperti pada cara berikut.

Jadi, notasi faktorial untuk persamaan (n+2) × (n+1) × n × (n-1) adalah (n + 2)!/(n-2)!
Jawaban: B
Contoh 2 – Soal Operasi dengan Notasi Faktorial
Nilai n yang memenuhi persamaan n+2/n! = 42 adalah ….
A. 3
B. 5
C. 8
D. 12
E. 21
Pembahasan:
Penyelesaian dari operasi bilangan yang memuat nilai faktorial seperti pada soal dapat diselesaikan seperti cara berikut.
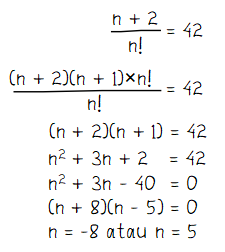
Akhir perhitungan menghasilkan dua nilai yaitu n = -8 dan n = 5. Diketahui bahwa bilangan bulat tidak memiliki definisi nilai faktorial. Sehingga nilai n = -8 tidak memenuhi persamaan, nilai n yang memenuhi persamaan adalah 5. Jadi, nilai n yang memenuhi persamaan n+2/n! = 42 adalah n = 5.
Jawaban: B
Oke, sekian penjabaran materi tentang notasi faktorial dan penjelasan mengenai nilai 0! = 1 dan 1! = 1. Terimakasih sudah mengunjungi idschool.net, semoga bermanfaat, sampai jumpa di artikel selanjutnya.
Baca Juga: Pengertian Permutasi, Kombinasi, dan Perbedaannya


n!/(n-3) cara mengerjakanya bagaimana kak