Polinomial atau suku banyak adalah deret bilangan yang memuat variabel, eksponen (pangkat), dan koefisien. Contoh suku banyak berderajat dua adalah P(x) = 3x2 + 5x + 19. Contoh suku banyak berderajat tiga adalah P(x) = x3 – 6x2 + 11x – 6. Derajat dalam suku banyak menyatakan pangkat tertinggi dari variabelnya.
Pembagian suku banyak adalah salah satu operasi untuk melakukan pembagian fungsi P(x) dengan suatu fungsi f(x). Bagaimana cara melakukan operasi pembagian suku banyak? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Pembagian suku banyak dengan cara bersusun
Cara melakukan operasi pembagian suku banyak dengan cara bersusun dilakukan seperti melakukan operasi pembagian bilangan biasa. Sebagai contoh, perhatikan operasi pembagian suku banyak P(x) = x2 + 6x – 10 oleh (x – 1) dengan cara bersusun seperti berikut.

Pertama, perhatikan bahwa persamaan P(x) = x2 + 6x – 10 mempunyai pangkat tertinggi 2, sedangkan pembaginya x – 1 mempunyai pangkat tertinggi 1.
Agar x2 pada P(x) = x2 + 6x – 10 dapat habis dikurang, sobat idschool perlu mengalikan x – 1 dengan x agar menghasilkan x2 – x. Dari sini, x2 bisa saling dikurangkan. Hasil pengurangan x2 + 6x dengan x2 – x adalah 7x.
Turunkan nilai –10 sehingga bilangan yang harus dibagi selanjutnya adalah 7x – 10. Untuk mendapatkan nilai 7x, sobat idschool perlu mengalikan x – 1 dengan 7, hasilnya adalah 7x – 7. Selanjutnya, kurangkan 7x – 10 dan 7x – 7 yaitu –3.
Dari langkah pembagian yang dilakukan diperoleh bahwa hasil bagi suku banyak P(x) = x2 + 6x – 10 adalah h(x) = x + 7 dan sisa pembagiannya adalah S(x) = –3. Suku banyak P(x) secara matematis dapat dinyatakan melalui persamaan P(x) = (x – k) · (7x – 7) – 3.
Sebagai contoh lain, perhatikan cara melakukan operasi pembagian fungsi P(x) = x2+ 7x + 1 oleh 3x – 2 berikut.

Dari hasil operasi pembagian suku banyak P(x) = x2+ 7x + 1 oleh 3x – 2 dengan cara bersusun diperoleh hasil bagi H(x) = 1/3x + 23/3 = 1/3(x + 23/3) dan S(x) = 55/9. Dengan demikian, suku banyak P(x) dapat dinyatakan dalam persamaan P(x) = (3x – 2) · 1/3(x + 23/3) + 55/9.
Bentuk pembagi suku banyak dapat juga berupa suku banyak berderajat dua (ax2 + bx + c). Misalnya pada pembagian suku banyak P(x) = x3 – 2x2 + 6x + 7 oleh x2 – x + 1.
Operasi pembagian suku banyak P(x) = x3 – 2x2 + 6x + 7 oleh x2 – x + 1 dengan cara bersusun dilakukan seperti langkah penyelesaian di bawah.
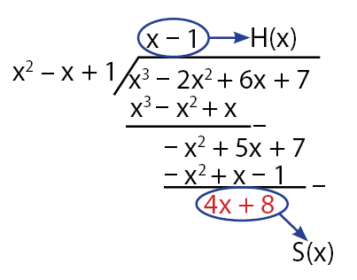
Dari langkah perhitungan diperoleh hasil bagi dari x3 – 2x2 + 6x + 7 oleh x2 – x + 1 adalah H(x) = x – 1 dan sisa pembagiannya adalah S(x) = 4x + 8. Dengan demikian, suku banyak P(x) = x3 – 2x2 + 6x + 7 memenuhi persamaan P(x) = (x2 – 2 + 1) · (x – 1) + 4x + 8.
Baca Juga: Teorema Sisa dan Teorema Faktor Pada Suku Banyak
Pembagian suku banyak dengan skema Horner
Cara lain untuk melakukan pembagian suku banyak adalah menggunakan skema horner. Pada skema Horner, perhitungan dilakukan menggunakan koefisien dari setiap suku banyak.
Misalnya pada pembagian suku banyak P(x) = ax2 + bx + 10 oleh (x – k). Langkah operasi yang dilakukan denga skema Horner mengikut aturan berikut.

Pada skema horner, baris terakhir adalah hasil yang akan digunakan. Satu suku terakhir pada baris terakhir merupakan sisa, sementara suku-suku lainnya merupakan hasil bagi. Untuk skema Horner di atas memiliki sisa pembagian S(x) = c + bk + ak2 dan hasil bagi ax + (b + ak).
Contoh penggunaan skema Horner di bawah untuk menentukan hasil bagi f(x) = x2 + 6x – 10 oleh (x – 1).

Diperoleh hasil pembagian suku banyak f(x) = x2 + 6x – 10 oleh (x – 1) adalah H(x) = x + 7 dan sisa pembagiannya adalah S(x) = –3. Hasil ini sesuai dengan apa yang diperoleh untuk pembagian suku banyak dengan cara bersusun pada penyelesaian sebelumnya, bukan?
Penggunaan skema Horner pada pembagian suku banyak lainnya akan ditunjukkan untuk mencari hasil bagi dan sisa pembagian suku banyak P(x) = x2+ 7x + 1 oleh 3x – 2.
Bentuk pembagi (ax + b) memiliki nilai k = – b/a. Jadi, nilai k untuk 3x – 2 → k = 2/3. Proses pembagian dengan sekma Horner dilakukan seperti berikut.
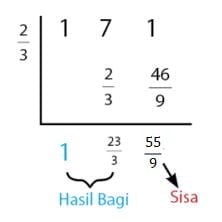
Persamaan pembagian suku banyak P(x) oleh (ax + b) adalah P(x) = (ax + b) · H(x)/a + S(x). Dari skema Horner di atas diperoleh hasil bagi H(x) = x + 23/3 dan sisa pembagian S(x) = 55/9.
Sehingga suku banyak f(x) dapat dinyatakan menjadi seperti berikut.
P(x) = (3x – 2) · (x + 23/3)/3 + 55/9
P(x) = 1/3(3x – 2)(x + 23/3) + 55/9
Hasil di atas juga sama seperti hasil dan sisa pembagian P(x) = x2+ 7x + 1 oleh 3x – 2 dengan cara bersusun.
Untuk pembagian suku banyak P(x) = x3 – 2x2 + 6x + 7 oleh x2 – x + 1 tidak bisa dilakuan dengan skema horner. Kondisi ini dikarenakan pembagi suku banyak yaitu persamaan kuadrat x2 – x + 1 memiliki nilai diskriminan D < 0 sehingga dapat disimpulkan persamaan kuadrat tidak mimiliki akar-akar real.
Pada skema Horner membutuhkan akar bilangan real untuk melakukan operasi pembagian suku banyak. Namun pada soal ini, pembagi suku banyak tidak memiliki akar real. Sehingga skema Horner tidak bisa dilakukan untuk menentukan hasil bagi dan sisa pembagian suku banyak x3 – 2x2 + 6x + 7 oleh x2 – x + 1.
Baca Juga: Induksi Matematika
Selanjutnya, agar lebih paham cara pembagian suku banyak dapat mengerjakan beberapa soal latihan di bawah.
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal Pembagian Suku Banyak
Sisa dari pembagian fungsi suku banyak f(x) = x4 + x3 – 2x2 + x + 2 oleh x + 2 adalah ….
A. 0
B. 1
C. 2
D. 3
E. 4
Pembahasan:
Sisa dari pembagian fungsi suku banyak f(x) = x4 + x3 – 2x2 + x + 2 oleh x + 2 (k = –2) dapat diketahui dengan skema Horner seperti penyelesaian berikut.
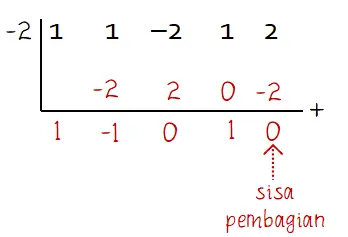
Jadi, sisa dari pembagian fungsi suku banyak f(x) = x4 + x3 – 2x2 + x + 2 oleh x + 2 adalah 0.
Jawaban: A
Contoh 2 – Soal Pembagian Suku Banyak
Hasil bagi dan sisa pembagian jika suku banyak f(x) = x4 – 3x3 – 5x2 + x – 6 dibagi oleh x2 – x – 2 berturut-turut adalah ….
A. x2 + 2x + 5 dan –8x – 16
B. x2 – 2x + 5 dan 8x + 16
C. x2 – 2x – 5 dan –8x + 16
D. x2 + 2x + 5 dan –8x + 16
E. x2 – 2x – 5 dan –8x – 16
Pembahasan:
Pertama perlu untuk mendapatkan bilangan riil pembuat nol dari pembagi suku banyak yaitu x2 – x – 2. Caranya dengan melakukan pemfaktoran untuk persamaan kuadrat x2 – x – 2 = 0 seperti berikut.
Nilai x pembuat nol bilangan penyebut:
x2 – x – 2 = 0
(x – 2)(x + 1) = 0
Diperoleh P1 = (x – 2) dan P2 = (x + 1), nilai k yang digunakan ada dua yaitu k = x1 = 2 dan k = x2 = –1. Hasil bagi dan sisa pembagian suku banyak dapat diketahui dengan skema Horner untuk pembagian f(x) = x4 – 3x3 – 5x2 + x – 6 oleh x2 – x – 2 berikut.
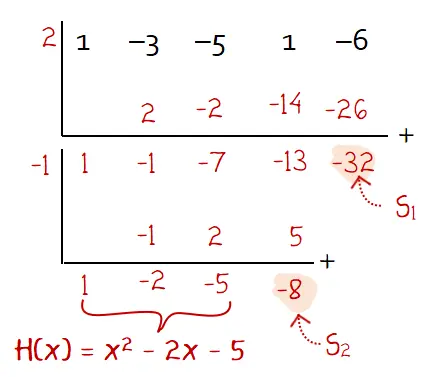
Dari skema horne di atas dapat diketahui hasil bagi dan sisa pembagian seperti berikut.
*keterangan: a = koefisien x2 pada pembagi suku banyak (x2 – x – 2), a = 1
Sisa pembagian: Sisa = S2 · P1 + S2
S(x) = –8(x – 2) + (–32)
S(x) = –8x + 16 – 32
S(x) = –8x – 16
Jadi, hasil bagi dan sisa pembagian suku banyak x4 + 4x3 + x2 – 5x + 7 oleh x + 2 berturut-turut adalah x2 – 2x – 5 dan –8x – 16.
Jawaban: E
Sekian pembahasan mengenai pembagian suku banyak dengan cara pembagian bersusun dan skema Horner. Terima kasih sudah berkunjung di idschool.net, semoga bermanfaat.

Buat pembagian suku banyak cara horner dengan pembagi yang dapat difaktorkan, itu salah jawaban dan caranya. Setelah di kali antara hasil bagi-pembagi-ditambah sisa itu masih salah hasilnya.
Halo Fikar, sudah ada revisi, terimakasih atas koreksi dan kunjungannya. Salam sukses selalu!