Bahasan perkalian vektor dapat berupa perkalian vektor dengan suatu skalar atau perkalian vektor dengan vektor. Pengertian dari vektor sendiri adalah besaran yang memiliki nilai dan arah. Sedangkan besaran yang hanya memiliki nilai saja disebut skalar. Hasil dari perkalian vektor adalah vektor yang mengalami perubahan sehingga dapat dikatakan menjadi vektor baru. Perubahan yang terjadi dari perkalian skalar vektor dapat lebih panjang, lebih pendek, atau sama dengan vektor awal.
Perkalian skalar vektor juga dapat mengubah arah vektor awal, bisa searah atau berlawanan. Misalnya pada perkalian skalar vektor dengan nilai skalar k = 2 akan menghasilkan vektor yang memiliki ukuran 2 kali vektor awal.

Bagaimana cara melakukan perkalian vektor dengan skalar? Bagaimana cara perkalian vektor dengan vektor? Sobat idscool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Perkalian Vektor dengan Skalar
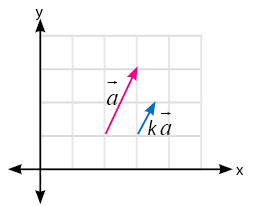
Perkalian skalar dengan suatu vektor dapat digambarkan secara geometri. Misalkan terdapat k yang merupakan anggota bilangan real dan terdapat vektor a yang meruakan sebuah vektor. Hasil perkalian skalar k dengan vektor a ditulis sebagai k · a. Arti penulisan k · a memiliki arti bahwa suatu vektor yang memiliki panjang k kali panjang vektor a.
Hasil perkalian vektor dengan skalar dapat memiliki beberapa kemungkinan bergantung nilai skalar k yang menjadi faktor pengali. Beberapa kemungkinan yang dapat terjadi pada perkalian vektor dengan skalar diberikan seperti pada pada beberapa nilai k berikut.
Untuk k > 1 maka k · a searah dengan vektor a dan diperpanjang.

Untuk k = 1 maka k · a sama dengan vektor a.

Untuk 0 < k < 1 maka k · a searah dengan panjang vektor a yang lebih diperpendek
Untuk -1 < k < 0 maka k · a berlawanan arah dengan panjang vektor a yang lebih diperpendek

Untuk k = -1 maka k · a berlawanan arah dengan panjang yang sama

Untuk k< -1 maka k · a berlawanan arah dengan vektor a dan lebih panjang

Perkalian vektor denga skalar juga dapat dilakukan secara aljabar yaitu dengan cara mengalikan semua unsur pada vektor dengan nilai pengalinya. Jika k adalah suatu konstanta real dan diketahui koordinat vektor a maka vektor b yang merupakan hasil perkalian antara k dan vektor a dituliskan sebagai b = k · a
Sebagai contoh:terdapat skalar dengan nilai k = 2 dan vektor a = 2x + 3y – 5z, perkalian vektor a dengan skalar k dapat dilakukan seperti cara berikut.
b = k · a
b = 2 · (2x + 3y – 5z)
b = 4x + 6y – 10z
Perkalian vektor dengan skalar memiliki beberapa sifat yang diberikan seperti pada daftar berikut.

Baca Juga: Perbandingan Vektor pada Sebuah Ruas Garis
Perkalian Vektor dengan Vektor
Perkalian vektor dengan vektor dibedakan untuk perkalian silang (cross product) dan perkalian titik (dot product). Kedua jenis perkalian memiliki aturan yang perlu diikuti, sobat idschool hanya perlu mengikuti bagaimana aturan yang berlaku.
Untuk bahasan di bawah merupakan perkalian dot vektor.
Operasi perkalian vektor dengan vektor dilakukan dengan cara mengalikan semua bilangan dengan arah yang sama. Misalnya diketahui suatu vektor dinyatakan dalam persamaan vektor u = 3i + 8j + k dan vektor lain katakanlah vektor v = i + 5j + 2k. Pada dua contoh persamaan vektor yang diberikan memiliki arah yang dinyatakan dalam i, j, dan k. Arah yang sama ditunjukkan oleh huruf yang sama seperti i dengan i, j dengan j, atau k dengan k.
Secara umum, rumus perkalian vektor dengan vektor dinyatakan seperti pada persamaan-persamaan di bawah
1) Perkalian skalar dua vektor di ruang dimensi dua:
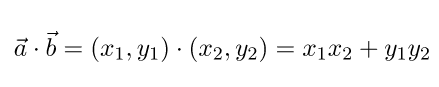
2) Perkalian skalar dua vektor di ruang dimensi tiga:

Perkalian antara dua vektor memenuhi sifat-sifat perkalian berikut.

Pada perkalian vektor a dan vektor b membentuk suatu sudut yang besarnya dipengaruhi oleh panjang vektor keduanya. Jika besar sudut antara vektor a dan vektor b diketahui maka perkalian kedua vektor tersebut dapat dihitung dengan rumus berikut.

Baca Juga: Cara Menentukan Vektor yang Saling Sejajar dan Tegak Lurus
Contoh Soal dan Pembahasan
Beberapa contoh di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Perkalian Vektor
Diketahui vektor a = 5i + 3j – 8k dan vektor b = 3i + 4j – 2k. Hasil kali skalar vektor a · b adalah ….
A. 11
B. 27
C. 33
D. 43
E. 53
Pembahasan:
Menghitung hasil kali skalar vektor a · b:
a · b = 5 × 3 + 3 × 4 + (–8) × (–2)
= 15 + 12 + 16
= 43
Jawaban: D
Contoh 2 – Soal Perkalian Vektor
Jika diketahui nilai panjang vekor | p | = 2, | q | = 3, | p ‒ q | = √7 maka nilai | p + q | adalah ….
A. √13
B. √15
C. √17
D. √19
E. √21
Pembahasan:
Mencari nilai 2pq:
| p ‒ q | = √7
| p ‒ q |2 = 7
| p || p | ‒ 2 | p | | q | + | q | | q | = 7
2 × 2 ‒ 2 | p || q | + 3 × 3 = 7
4 – 2 | p || q | + 9 = 7
2 | p || q | = 9 + 4 – 7
2 | p || q | = 6
Mencari nilai | p + q |:
| p + q |2 = p || p | + 2 | p | | q | + | q | | q |
| p + q |2 = 22 + 6 + 32
| p + q |2 = 4 + 6 + 9
| p + q |2 = 19
| p + q | = √19
Jawaban: D

kak ini gimana ya cara penyelesaiannya
Hitunglah perkalian scalar vector = 3i+ 4k dan v=-i +4j-5k
Kak ini cara nya gimna?
Dua vektor memiliki nilai masing masing 3N dan 4N. Tentukan hasil kali skalar dua vektor trsebut jika sudut yg dibentuk kedua vektor adalah 30°
Ditentukan a = i – 3j + 4k dan b = 5i – k Tentukanlah a x b dan b x a
Penyelesaian :
a x b =
gimana ya ka?
kak gimana nyelesaikan tugas ini?
1.dik.vektor a=3i-4k dan vektor b=2i-2j
dit: sinus sudut antara kedua vektor
tolong yah kak:v
Halo Nola, kamu bisa mencarinya dengan menentukan nilai cos nya terlebih dahulu. Setelah itu kamu bisa menentukan nilai sin nya.
a=3i-4k maka |a| = V3^{2} + 4 ^{2} = V25 = 5
b=2i-2j maka |b| = V2^{2} + 2^{2} = V8 = 2V2
Mencari besar sudut:
a.b = |a||b| cos A
3×2 + (-4)(-2) = 5 x 2V2 x cos A
6 + 8 = 10V2 x cos A
6 + 8 = 10V2 x cos A
14 = 10V2 x cos A
cos A = 14/10V2
diperoleh: sisi samping = 14 dan sisi miring = 10V2
Mencari sisi depan:
= V(10V2)^{2} – 14^{2}
= V 200 – 196
= V4
= 2
Jadi, sinus antara kedua vektor tersebut adalah
sin A = sisi depan/sisi miring
sin A = 2/10V2 = 2/5 . V2
Keterangan: V = akar
Semoga membantu :)
Kak gimana cara mencari perkalian titik antara dua vektor a dan b(a.b) dan perkalian silang antara a dan b (axb) dari vektor a=3i+j+2k dan b=i-2j-4k