Refleksi adalah pencerminan terhadap suatu sumbu. Untuk refleksi vertikal, pencerminan dilakukan terhadap sumbu x. Sementara untuk refleksi horizontal, pencerminan dilakukan terhadap sumbu y.
Objek yang mengalami refleksi dapat berupa titik, garis, atau kurva. Namun pada dasarnya, refleksi garis dan kurva merupakan refleksi setiap titik yang terdapat pada suatu garis atau kurva.
Pencerminan titik A(x, y) terhadap sumbu x (refleksi vertikal) adalah titik A'(x, –y). Sedangkan pencerminan terhadap sumbu y (refleksi horizontal) adalah titik A'(–x, y).
Bagaimana untuk pencerminan pada garis dan kurva? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Refleksi Vertikal
Refleksi vertikal adalah pencerminan terhadap sumbu x. Pada refleksi vertikal, setiap nilai absis akan tetap atau tidak mengalami perubahan (x’ = x). Sedangkan nilai ordinat karena refleksi vertikal akan menjadi bilangan lawannya (y’ = –y).
Dengan demikian dapat diketahui bahwa hasil refleksi vertikal dari fungsi y = f(x) adalah y’ = –f(x). Sebagai contoh, refleksi vertikal dari fungsi y = f(x) = 2x2 – 5x + 3 adalah y’ = –(2x2 – 5x + 3) = –2x2 + 5x – 3.
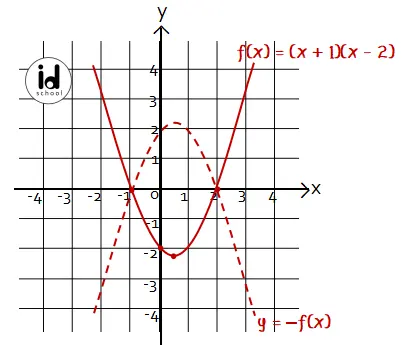
Contoh lainnya, hasil pencerminan fungsi f(x) = (x + 1)(x – 2) terhadap sumbu x adalah y’ = –f(x) = –(x + 1)(x – 2). Kurva f(x) = (x + 1)(x – 2) memiliki bentuk parrabola terbuka ke atas. Sedangkan kuva y’ = –f(x) merupakan hasil refleksi vertikal dari f(x) seperti yang terlihat pada gambar di bawah.
Baca juga: Cara Menggambar Grafik Fungsi Kuadrat (Kurva Parabola)
Refleksi Horizontal
Refleksi horizontal adalah pencerminan terhadap sumbu y. Setiap titik yang mengalami pencerminan terhadap sumbu y akan merubah nilai absis menjadi lawannya (x’ = –x), sementara nilai ordinat tidak berubah (y’ = y).
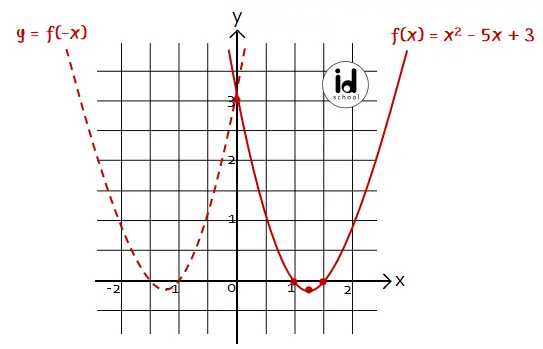
Sehingga dapat diketahui bahwa hasil refleksi horizontal y = f(x) adalah y’ = f(–x). Contohnya, refleksi dari y = 2x2 – 5x + 3 terhadap sumbu y adalah y’ = 2(–x)2 – 5(–x) + 3 = 2x2 + 5x + 3. Gambar kurva y = 2x2 – 5x + 3 dan hasil pencerminannya terhadap sumbu y terlihat seperti berikut.
Baca Juga: Rumus Translasi Vertikal dan Horizontal + Pembahasan Soalnya
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman materi refleksi vertikal dan horizontal. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Gunakanlah pembahasan soal yang diberikan sebagai tolak ukur keberhasilan mengerjakan soal! Selamat berlatih.
Soal 1 – Menentukan fungsi yang dihasilkan
Jika y = x2 + 2x – 1, tentukan fungsi yang dihasilkan dari
a) y = –f(x)
b) y = –f(–x)
Jawab:
a) y = –f(x)
y = –(x2 + 2x – 1)
y = –x2 – 2x + 1
b) y = –f(–x)
y = –((–x)2 + 2(–x) – 1)
y = –(x2 – 2x – 1) = –x2 + 2x + 1
Soal 2 – Gambar grafik fungsi
Diketahui f(x) = x(x + 1)(x – 2), gambarlah grafik fungsi berdasarkan:
a) 1 + f(–x)
b) –f(x + 5)
Jawab:
a) 1 + f(–x) → diperoleh dari grafik f(x) yang dicerminkan terhadap sumbu y (refleksi horizontal) kemudian digeser satu satuan ke atas.
b) –f(x + 5) → diperoleh dari grafik f(x) yang mengalam translasi horizontal sebanyak 5 satuan ke kiri kemudian dicerminkan terhadap sumbu x (refleksi vertikal).
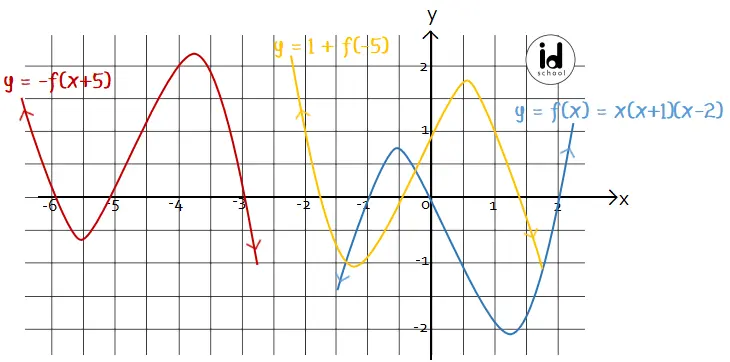
Grafik fungsi f(x) = x(x + 1)(x – 2) memiliki tiga titik potong dengan sumbu x yaitu pada titik (0, –1); (0, 0); dan (0, 2). Tiga kurva dari fungsi f(x), 1 + f(–x), dan –f(x + 5) terdapat pada gambar berikut.
Soal 3: Refleksi Vertikal dan Horizontal
Terdapat suatu grafik fungsi y = (x + 2)4 + 1. Jika grafik fungsi tersebut direfleksikan secara horizontal dan vertikal, bagaimana prosedur menentukan hasil refleksinya?
Jawab:
Refleksi secara horizontal: y= f(x) → y’ = f(–x)
Diketahui: f(x) = (x + 2)4 + 1
Maka, y’ = (–x + 2)4 + 1
y’ = (2 – x)4 + 1
Refleksi secara vertikal = f(x) → y’ = –f(x)
Diketahui: f(x) = (x + 2)4 + 1
Maka,
y’ = –[(x + 2)4 + 1]
y’ = –(x + 2)4 – 1
Soal 4 – Fungsi hasil refleksi vertikal dan horizontal
Tentukan persamaan grafik setelah ditransformasikan berikut!
a) y = 2x4 setelah direfleksikan terhadap sumbu x
b) y = 2x + 1 – 3 setelah direfleksikan terhadap sumbu y
c) y = 3–x + 1 setelah direfleksikan terhadap sumbu x
Jawab:
a) Refleksi terhadap sumbu x: y = f(x) → y’ = –f(x)
Untuk y = f(x) = 2x4 maka y’ = –2x4
Jadi, hasil refleksi vertikal dari fungsi y = 2x4 adalah y’ = 2x4.
b) Refleksi terhadap sumbu y: y = f(x) → y’ = f(–x)
Untuk y = f(x) = 2x + 1 – 3 maka
y’ = 2–x + 1 – 3 = 21 · 2–x – 3
Jadi, hasil refleksi horizonral dari fungsi y = 2–x + 1 – 3 adalah y’ = 2/2x – 3.
c) Reflesi vertikal: y = f(x) → y’ = –f(x)
Untuk y = f(x) = 3–x + 1 maka y’ = –(3–x + 1)
y’ = –3–x – 1
Jadi, refleksi fungsi y = 3–x + 1 terhadap sumbu x adalah y’ = –3–x – 1.
Soal 5 – Menentukan grafik fungsi hasil refleksi
Diketahui suatu fungsi y = f(x) seperti gambar di bawah ini.
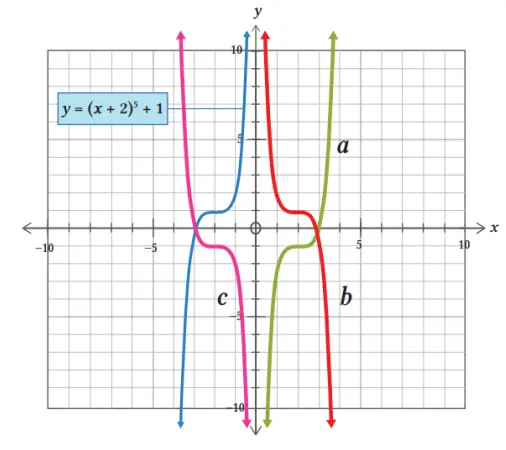
Tunjukkan fungsi yang ditunjukkan pada grafik a, b, dan c.
Jawab:
Grafik b adalah hasil pencerminan terhadap sumbu y (refleksi horizontal) dari grafik y = (x + 2)5 + 1. Jadi, fungsi yang sesuai untuk grafik pada gambar b adalah yb’ = (–x + 2)5 + 1 → yb’ = (2 – x)5 + 1.
Grafik a adalah hasil refleksi vertikal grafik b, sehingga fungsi yang sesuai untuk gambar grafik a adalah ya’ = –[(2 – x)5 + 1] → ya’ = –(2 – x)5 – 1.
Sementara grafik c adalah hasil refleksi vertikal dari grafik y = (x + 2)5 + 1. Jadi, fungsi yang sesuai untuk gambar grafik c adalah yc’ = –[(x + 2)5 + 1] → yc’ = –(x + 2)5 – 1.
Diperoleh fungsi yang ditunjukkan pada grafik a, b, dan c berturut-turut adalah ya’ = –(2 – x)5 – 1; yb’ = (2 – x)5 + 1; dan yc’ = –(x + 2)5 – 1.
Sekian ulasan mengenai refleksi vertikal dan horizontal. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
