Diketahui ada dua macam dilatasi yaitu dilatasi vertikal dan horizontal. Dilatasi adalah perkalian suatu objek terhadap faktor skala k. Nilai k merupakan bilangan real. Perkalian sebuah kurva dengan nilai k menghasilkan kurva menjadi lebih besar atau lebih kecil.
Sebagai contoh, grafik fungsi y = x2 – 4x – 5 akan menjadi y = 2(x2 – 4x – 5) karena dilatasi vertikal. Sedangkan grafik fungsi y = x2 – 4x – 5 akan menjadi y = (2x)2 – 4(2x) – 5 karena dilatasi horizontal.
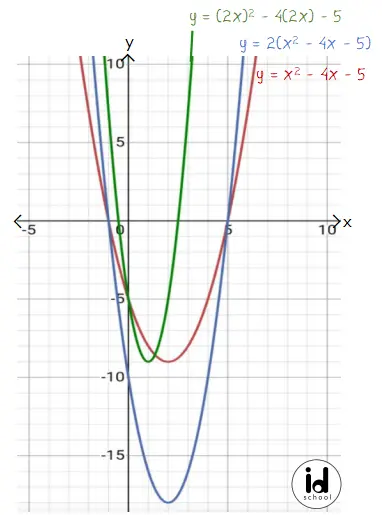
Pembahasan soal dilatasi vertikal dan horizontal ada pada detail di bawah.
Daftar isi:
Rumus Dilatasi Vertikal dan Horizontal
Ada dua bentuk dilatasi dengan faktor k yaitu dilatasi vertikal dan dilatasi horizontal. Penjelasan kedua bentuk dilatasi ada di bawah.
1) Dilatasi vertikal dengan faktor k
Dilatasi vertikal adalah dilatasi yang dilakukan sejajar sumbu y. Hasil translasi y = f(x) karena dilatasi vertikal dengan faktor skala k adalah y = k · f(x).
- Pada y = k · f(x) berlaku:
- Untuk nilai k > 1, grafik y = f(x) menjadi lebih besar secara vertikal
- Untuk nilai 0 < k < 1, grafik y = f(x) menjadi lebih kecil secara vertikal
Saat nilai absisnya tetap. Dilatasi vertikal membuat setiap ordinat dikalikasi dengan dengan faktor skala k.
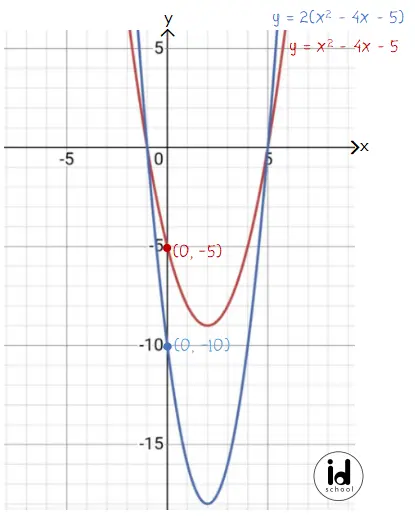
Contohnya pada fungsi y = x2 – 4x – 5. Dilatasi vertikal dengan faktor skala k = 2 mmenghasilkan fungsi y = 2(x2 – 4x – 5). Untuk nilai x yang sama, nilai y akan menjadi dua kalinya.
Misalnya saat nilai x = 0, nilai y = –5 menjadi y’ = –10 karena dilatasi vertikal dengan faktor skala k = 2.
Baca Juga: Cara Menggambar Grafik Fungsi Kuadrat (Kurva Parabola)
2) Dilatasi horizontal dengan faktor k
Dilatasi horizontal adalah dilatasi dilakukan dengan faktor skala k yang sejajar sumbu x. Hasil dilatasi horizontal y = f(x) adalah grafik y = f(k · x). Dengan nilai k adalah bilangan real positif.
Dilatasi horizontal membuat setiap nilai absis dibagi dengan faktor skala k.
- Pada y = f(k · x) berlaku:
- Untuk k > 1, grafik y = f(x) yang diperkecil secara horizontal
- Untuk 0 < k < 1, grafik y = f(x) yang diperbesar secara horizontal
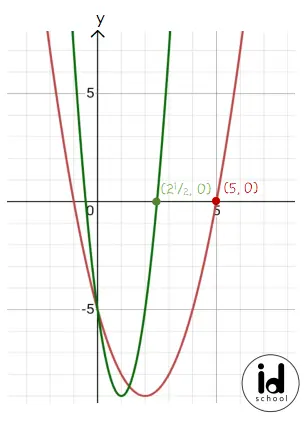
Contohnya pada fungsi y = x2 – 4x – 5. Dilatasi horizontal dengan faktor skala k = 1/2 mmenghasilkan fungsi y = (2x)2 – 4(2x) – 5.
Saat nilai y sama, nilai x akan dibagi dua. Misalnya saat y = 0, dari nilai x = 5 menjadi x’ = 21/2 karena dilatasi horizontal dengan faktor skala k = 1/2.
Baca Juga: Rumus Translasi Sejajar Sumbu x dan Sumbu y
Pembahasan Soal Dilatasi Vertikal dan Horizontal
Pembahasan soal dilatasi vertikal dan horizontal ada pada uraian di bawah. Semoga bermanfaat!
Soal 1 – Tentukan hasil dilatasi dari fungsi berikut!
Diketahui f(x) = x3. Tentukan hasil dilatasi dari fungsi berikut.
a. y = 6f(x)
b. y = f(4x)
Jawab:
a) y = 6 · f(x)
y = 6 · x3
y = 6x3
b) y = f(4x)
y = (4x)3
y = 64x3
Soal 2 – Kurva hasil dilatasi vertikal dan horizontal
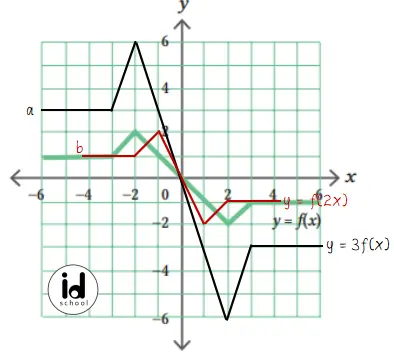
Diketahui suatu fungsi y = f(x) yang ditunjukkan pada gambar di bawah ini.
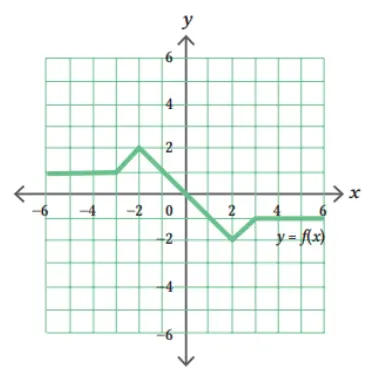
Gambarlah grafik lain berdasarkan fungsi berikut.
a. y = 3f(x)
b. y = f(2x)
Jawab:
Transformasi grafik:
a) y = 3f(x) → Nilai y menjadi tiga kalinya, nilai x tetap. Kurva akan membesar secara vertikal dengan skala 3 satuan.
b) y = f(2x) → Nilai x menjadi setengah kalinya (nilai x dibagi dua), nilai y tetap. Kurva f(x) akan mengecil secara horizontal dengan skala 1/2 satuan.
Gambar grafik y = 3f(x) dan y = f(2x) yang sesuai:
Baca Juga: Transformasi Geometeri [Translasi, Refleksi, Rotasi, dan Dilatasi]
Soal 3 – Tentukan persamaan setiap grafik setelah diberikan transformasi.
Tentukan persamaan setiap grafik setelah diberikan transformasi.
a. y = 3x2 setelah dilatasi sejajar sumbu y dengan skala 2
b. y = x3 – 1 setelah dilatasi sejajar sumbu y dengan skala 3
c. y = 4x + 6 setelah dilatasi sejajar sumbu y dengan skala 1/2
Jawab:
Rumus dilatasi sejajar sumbu y: y = f(x) → y’ = k · f(x)
a) y = 3x2; k = 2
→ y’ = 2 · 3f(x) = 6f(x)
b) y = x3 – 1; k = 3
→ y’ = 3(x3 – 1)
c) y = 4x + 6; k = 1/2
→ y’ = 1/2(4x + 6)
Soal 4 – Tunjukkan transformasi yang memetakan fungsi berikut.
Tunjukkan transformasi yang memetakan fungsi berikut.
a. y = x2 + 2x – 5 menjadi grafik y = 4x2 + 4x – 5
b. y = x2 – 3x + 2 menjadi grafik y = 3x2 – 9x + 6
c. y = 2x + 1 menjadi grafik y = 2x+1 + 2
Jawab:
a) Diketahui y = x2 + 2x – 5
Sehingga,
y’ = 4x2 + 4x – 5
y’ = (2x)2 + 2(2x) – 5
→ y’ = f(2·x) merupakan dilatasi y = x2 + 2x – 5 sejajar sumbu x dengan faktor skala k = 1/2
b) Diketahui y = x2 – 3x + 2
Sehingga,
y’ = 3(x2 – 3x + 2)
→ y’ = 3 · f(x) merupakan dilatasi y = x2 – 3x + 2 sejajar sumbu y dengan faktor skala k = 3
c) Diketahui y = 2x + 1
Sehingga,
y’ = 2x+1 + 2 = 2 · 2x + 2
y’ = 2 · (2x + 1)
→ y’ = 2 · f(x) merupakan dilatasi y = 2x + 1 sejajar sumbu x dengan faktor skala 2.
Sekian ulasan rumus dilatasi vertical dan horizontal. Terima kasih sudah mengunjungi idschool(dot)net. Semoga bermanfaat!
