Ketinggian maksimum peluru saat ditembakkan dengan lintasan parabola dicapai saat berada pada titik terjauh dari tanah. Ketinggian maksimum peluru merupakan titik puncak dari lintasan parabola yang dilalui peluru. Setelah peluru mencapai ketinggian maksimum, peluru tersebut akan bergerak dengan lintasan melengkung ke arah bawah. Rumus jarak dan ketinggian maksimum peluru dapat dicari dengan persamaan-persamaan yang berlaku pada gerak benda dengan bentuk lintasan parabola.
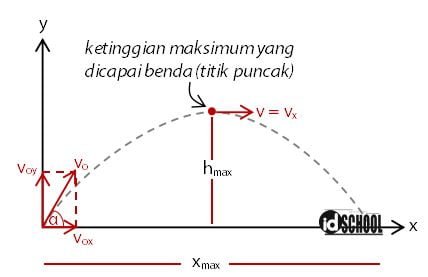
Sebuah peluru yang ditembakkan dengan sudut tertentu terhadap bidang horizontal akan bergerak dengan bentuk lintasan parabola. Setelah waktu t, peluru yang ditembakkan dengan kecepatan vo akan mencapai ketinggian maksimum. Selanjutnya, peluru akan terus melaju kembali dengan suatu kecepatan v dan berhenti serta mencapai jarak mendatar maksimum.
Baca Juga: Cara Mencari Titik Berat Benda
Rumus jarak mendatar maksimum (xmax) yang dicapai peluru dan ketinggian maksimum peluru (hmax) sama dengan xmax dan hmax pada benda dengan gerak parabola. Bagaimana bentuk rumus ketinggian maksimum peluru? Bagaimana cara menghitung jarak mendatar maksimum yang dapat dicapai peluru? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Ketinggian Maksimum Peluru atau Titik Puncak yang Dapat Dicapai
- Jarak Mendatar Maksimum yang Dapat Dicapai Peluru
- Contoh Soal dan Pembahasan
Ketinggian Maksimum Peluru atau Titik Puncak yang Dapat Dicapai
Benda yang dilemparkan dengan kecepatan awal vo dan sudut elevasi α tertentu akan mempunyai lintasan berbentuk parabola. Contoh benda yang mengalami gerak parabola adalah peluru yang ditembakkan dengan kecepatan dan sudut tertentu.
Dalam gerak parabola, gerak benda dapat diuraikan dalam dua sumbu yaitu pada sumbu x dan sumbu y. Pada sumbu x berlaku gerak lurus beraturan (GLB), sedangkan pada sumbu y berlaku gerak lurus berubah beraturan (GLBB).
Kecepatan gerak pada sumbu x (horizontal) merupakan gerak lurus beraturan yang memenuhi persamaan vx = vox = vocos α. Sehingga jarak mendatar yang ditempuh oleh sebuah benda ditentukan oleh persamaan x = vx⋅t = vot ⋅ cos α.
Sedangkan kecepatan gerak pada sumbu y (vertikal) merupakan gerak lurus berubah beraturan yang memenuhi vy = voy – gt = vo⋅sin α – gt. Posisi benda pada sumbu y dapat diketahui melalui persamaan y = voyt – 1/2gt2 atau y = vot⋅sin α – 1/2gt2.
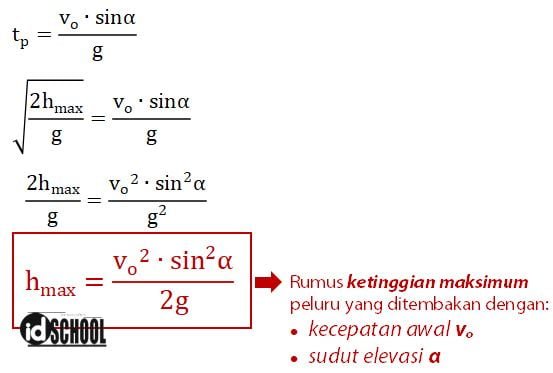
Ketinggian maksimum peluru yang ditembakkan dengan lintasan parabola terjadi saat kecepatan benda pada sumbu y sama dengan nol (vy = 0). Substitusi nilai vy = 0 pada persamaan vy = voy – gt akan menghasilkan persamaan waktu yang dibutuhkan untuk mencapai titik puncak (tp) seperti persamaan berikut.

Ketinggian benda pada titik tertinggi memenuhi persamaan hmax = 1/2gtp2 sehingga tp2 = 2hmax : g atau tp sama dengan akar dari 2hmax : g. Substitusi persamaan tp tersebut ke rumus tp = vo⋅sin α /g akan menghasilkan rumus hmax seperti berikut.
Baca Juga: Rumus Gaya Sentripetal dan Percepatan pada Benda dengan Gerak Melingkar
Jarak Mendatar Maksimum yang Dapat Dicapai Peluru
Waktu tempuh untuk mencapai titik terjauh atau jarak mendatar maksimal sama dengan dua kali waktu yang diperlukan untuk mencapai titik tertinggi (2tp). Jarak terjauh yang dicapai benda pada sumbu x (arah mendatar/horizontal) dapat dihitung melalui persamaan xmax. Di mana, persamaan tersebut dapat diperoleh melalui rumus jarak yaitu kecepatan dikali waktu yang dibutuhkan.
Sebuah peluru ditembakkan dengan kecepatan vo dan sudut elevasi α. Persamaan untuk mendapatkan jarak medatar maksimal (xmax) diberikan seperti langkah-langkah berikut.
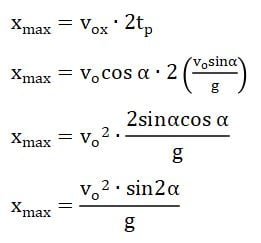
Jadi, persamaan yang dapar digunakan untuk menghitung jarak mendatar maksimum yang dapat dicapai peluru adalah sebagai berikut.

Baca Juga: Gerak Parabola dan Keterangannya
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara menghitung jarak dan ketinggian maksimum peluru dengan lintasan parabola. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Analisi Gerak Peluru dengan Gerak Parabola
Sebuah peluru yang ditembakkan dengan kecepatan Vo dan sudut elevasi α. Pada titik tertinggi, maka ….
A. tenaga kinetiknya nol
B. tenaga kinetiknya maksimal
C. tenaga potensialnya maksimal
D. tenaga totalnya maksimal
E. kecepatannya maksimal
Pembahasan:
Saat posisi benda berada di titik tertinggi pada lintasan berbentuk parabola memiliki kecepatan benda pada komponen vertikal vy = 0. Pada posisi yang sama, benda berada titip puncak atau berada pada ketinggian maksimum. Kecepatan mempengaruhi energi kinetik, sedangkan ketinggian mempengaruhi nilai energi potensial.
Sehingga, pada saat benda berada titik puncak memiliki energi kinetik minimal dan energi potensial maksimal. Jadi, pada titik tertinggi maka tenaga potensialnya maksimal.
Jawaban: C
Contoh 2 – Soal Ketinggian Maksimum Peluru
Sebuah peluru ditembakkan dengan kecepatan 60 m/s dan sudut elevasi 30°. Ketinggian maksimum peluru yang dapat dicapai adalah …. (g = 10 m/s2)
A. 30 m
B. 45 m
C. 50 m
D. 90 m
E. 100 m
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Kecepatan awal peluru: vo = 60 m/s
- Sudut elevasi: α = 30°
- Percepatan gravitasi: g = 10 m/s2
Menghitung ketinggian maksimum peluru:
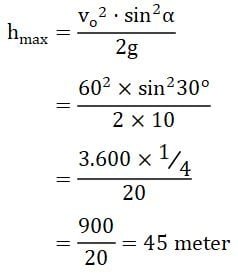
Jadi, Ketinggian maksimum yang dicapai peluru adalah 45 m.
Jawaban: B
Contoh 3 – Soal Jarak Mendatar Maksimum yang Dapat Dicapai Peluru
Sebuah peluru ditembakkan condong ke atas dengan sudut elevasi 30°. Dan kecepatan awal 30 m/s. Jika g = 10 m/s2, jarak mendatar terjauh yang dicapai peluru adalah ….
A. 45 m
B. 45√3 m
C. 90 m
D. 90√3 m
E. 180 m
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Sudut elevasi: α = 30°
- Kecepatan awal: vo = 30 m/s
- Percepatan gravitasi: g = 10 m/s2
Menghitung jarak mendatar terjauh yang dicapai peluru:
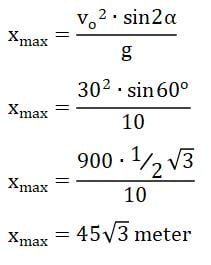
Jadi, jarak mendatar terjauh yang dicapai peluru adalah 45√3 m.
Jawaban: B
Baca Juga: Hubungan Roda-Roda (Sepusat, Bersinggungan, dan Dihubungkan oleh Tali)
Contoh 4 – Soal Ketinggian Maksimum Peluru
Sebuah benda dilempar dari suatu tempat yang tingginya 20 m di atas tanah dengan kecepatan 40 m/s dan sudut elevasi 60o terhadap horizontal. Jika g = 10 m/s2 maka tinggi maksimum yang dapat dicapai benda dari permukaan tanah adalah ….
A. 100 m
B. 80 m
C. 60 m
D. 40 m
E. 20 m
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Ketinggian mula-mula: ho = 20 m
- Kecepatan mula-mula: vo = 40 m/s
- Sudut elevasi: α = 60o
- Percepatan gravitasi: g = 10 m/s2
Menghitung ketinggian maksimum yang dicapai benda pada lintasan parabola:

Jadi, ketinggian maksimum terhadap permukaan tanah hmax = 20 + 60 = 80 meter.
Jawaban: B
Contoh 5 – Soal HOTS Benda dengan Gerak Parabola
Untuk menyalurkan bantuan kemanusiaan, sebuah pesawat kargo harus menjatuhkan kapsul besar berparasut kepada serombongan pengungsi. Jika hambatan udara sebelum parasut mengembang (yakni setelah 5 sekon dijatuhkan) diabaikan, ketinggian terbang minimal pesawat agar parasut kapsul telah mengembang di ketinggian 100 m sebelum mencapai permukaan adalah …. (g = 10 m/s2)
A. 185 m
B. 200 m
C. 215 m
D. 225 m
E. 250 m
Pembahasan:
Dari keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Ketinggian parasut: hp = 100 m
- Jarak waktu parasut dilemparkan sampai mengembang: t1 = 5s
- Percepatan gravitasi: g = 10 m/s2
- Ilustrasi yang sesuai dengan kondisi pada soal.

Selisih ketinggian sebelum parasut mengembang (t1 = 5 s):
ht = voyt + 1/2gt2
ht = 0 + 1/2 × 10 × 52
ht = 0 + 1/2 × 10 × 52 = 125 m
Ketinggian minimal pesawat:
hmin = ht + hp
hmin = 125 + 100 = 225 meter
Jadi, ketinggian terbang minimal pesawat agar parasut kapsul telah mengembang di ketinggian 100 m sebelum mencapai permukaan adalah 225 m.
Jawaban: D
Demikianlah tadi ulasan rumus ketinggian maksimum peluru dengan lintasan berbentuk parabola. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Percepatan Rata-Rata dan Sesaat
