Cara mencari titik berat benda 2 dimensi (luasan) dapat dilakukan melalui tiga langkah. Ketiga langkah pada cara mencari titik berat benda meliputi membagi bangun menjadi beberapa bagian, menentukan luas dan koordinat titik berat masing-masing bangun, serta menghitung letak titik berat benda menggunakan rumus titik berat benda.
Pengertian dari titik berat sendiri adalah titik keseimbangan sempurna atau sebuah pusat distribusi berat. Dengan kata lain, titik berat adalah titik dimana seakan akan berat seluruh benda terkosentrasi di satu titik tersebut. Sehingga, jika benda ditopang pada titik beratnya maka benda akan berada dalam keadaan seimbang.
Bagaimana cara mencari titik berat benda? Untuk mengetahui bahasan lebih lanjutnya, simak ulasan materi cara mencari titik berat benda dan contoh soal cara mencari titik berat benda beserta pembahasannya yang akan diberikan pada akhir bahasan.
Table of Contents
- Rumus Titik Berat Benda Homogen
- Contoh Cara Mencari Titik Berat Benda
- Contoh Soal Titik Berat Benda dan Pembahasan
Rumus Titik Berat Benda Homogen
Beberapa benda yang memiliki suatu bentuk bangun-bangun tertentu memiliki titik berat yang sesuai dengan tabel berikut.
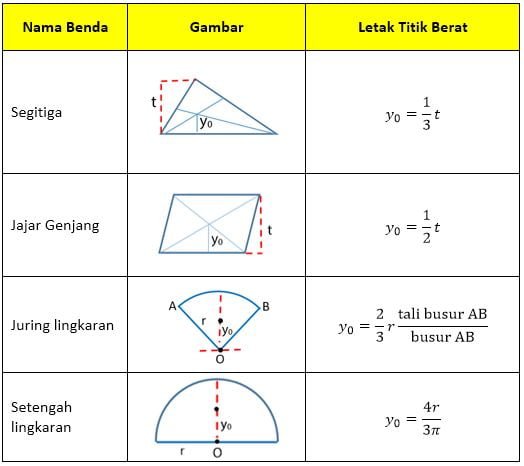
Rumus titik berat benda pada tabel di atas akan sobat idschool butuhkan pada cara mencari titik berat benda.
Selain itu, sobat idsccool juga membutuhkan rumus titik berat benda yang secara umum dapat dinyatakan dalam persamaan di bawah.

Rumus di atas digunakan ketika bangun tidak memiliki lubang/celah dalam bangun. Jika bentuk bangun memiliki lubang maka rumus menjadi pengurangan untuk bagian luas yang berlubang. Selanjutnya, penggunaan rumus titik berat bangun luasan di atas dapat dilihat seperti pada cara penyelesaian sebuah persoalan di bawah.
Baca Juga: Rumus Gerak Parabola dan Keterangannya
Contoh Cara Mencari Titik Berat Benda
Cara menghitung titik berat benda disesuaikan dengan bentuk benda tersebut. Pada proses perhitungan, sobat idschool perlu mengenali bentuk benda dan bagaimana cara menghitung luasnya. Selain dari perhitungan tersebut, proses perhitungan lainnya berupa operasi hitung bilangan penujumlahan, pengurangan, perkalian, dan pembagian.
Untuk lebih jelasnya perhatikan contoh cara mencari titik berat benda seperti bentuk berikut.
Soal: Carilah titik berat benda berikut!
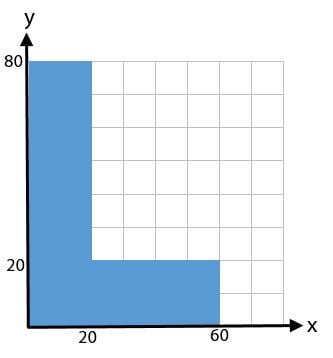
Langkah pertama, untuk mendapatkan titik berat pada bangun di atas, sobat idschool perlu membagi bangun ke dalam beberapa bagian. Dalam kasus ini, bangun tersebut akan dibagi menjadi dua bagian, seperti yang terlihat pada gambar di bawah.
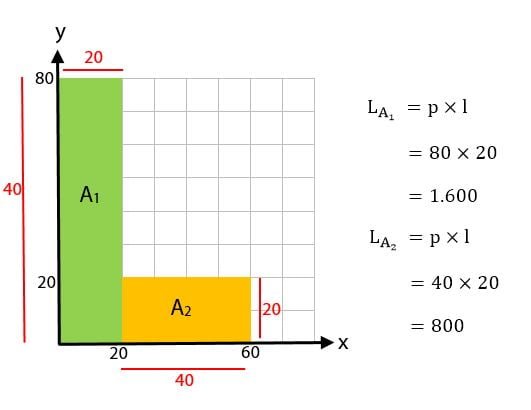
Diperoleh dua daerah yaitu daerah pertama (A1) dengan warna hijau dan daerah ke dua (A2) dengan warna kuning. Kedua daerah tersebut membentuk bangun persegi panjang. Dari dua bagian daerah tersebut, selanjutnya dapat dihitung luas kedua daerahnya. Luas daerah pertama sama dengan 1.600 satuan luas. Dan luas daerah kedua sama dengan 800 satuan luas.
Langkah berikutnya adalah menentukan koordinat titik berat dari kedua bangun. Caranya adalah dengan membuat diagonal dari keduanya dan mendapatkan titik koordinatnya.
Seperti yang terlihat pada gambar di bawah!
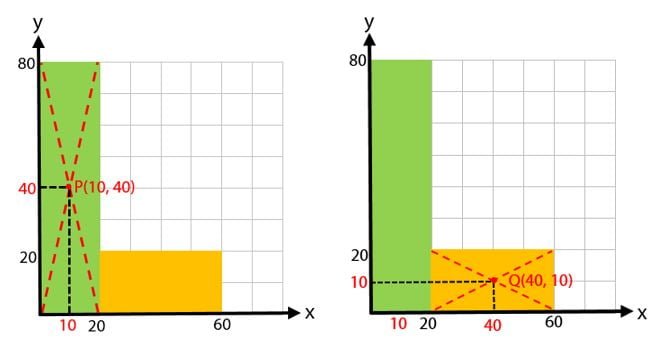
Diperoleh dua titik tengan untuk kedua bangun adalah titik P(10, 40) untuk bangun pertama dan titik Q(40, 10) untuk bangun ke dua.
Setelah mendapatkan luas masing – masing bangun dan titik berat untuk masing – masing bangun. Selanjutnya sobat idschool dapat menentukan titik berat benda yang diberikan menggunakan rumus titik berat benda yang sudah diberikan di atas.
Karena bangun yang diberikan hanya dibagi sampai dua bagian, maka sobat idschool hanya perlu menggunakan rumus berat benda sampai dua titik. Selanjutnya, perhatikan langkah pada cara mencari titik berat bendang berupa bangun luasan seperti pada cara berikut.
Mencari x0 (absis titik berat):
Mencari y0 (ordinat titik berat):
Jadi, diperoleh titik berat benda seperti pada soal adalah (20, 30) seperti yang ditunjukkan pada gambar di bawah.
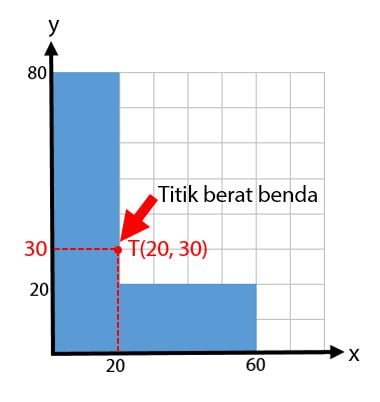
Baca Juga: Cara Mencari Titik Berat Benda Berupa Garis Lurus
Contoh Soal Titik Berat Benda dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan cara mencari titik beran benda/bangun luasan. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal dan Cara Mencari Titik Berat Benda
Perhatikan gambar di bawah!
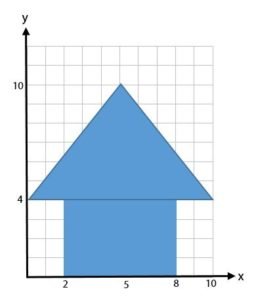
Koordinat titik berat gambar di atas adalah ….
A. 5; 4,2
B. 5; 5,0
C. 5; 5,1
D. 5; 6,0
E. 5; 6,1
Pembahasan:
Langkah pertama untuk menyelesaikan soal tersebut adalah membagi bangun menjadi beberapa bagian, dalam kasus ini, akan dibagi menjadi dua bagian yaitu bagian persegi panjang dan segitiga.
Luas daerah dari kedua bangun tersebut dapat dihitung seperti pada cara penyelesaian berikut.

Diperoleh luas bangun pertama (bangun segitiga) adalah 30 satuan luas, sedangkan luas bangun kedua (persegi panjang) adalah 24 satuan luas.
Selanjutnya atau langkah kedua adalah mencari titik berat koordinat untuk masing-masing bangun seperti yang ditunjukkan pada cara berikut.
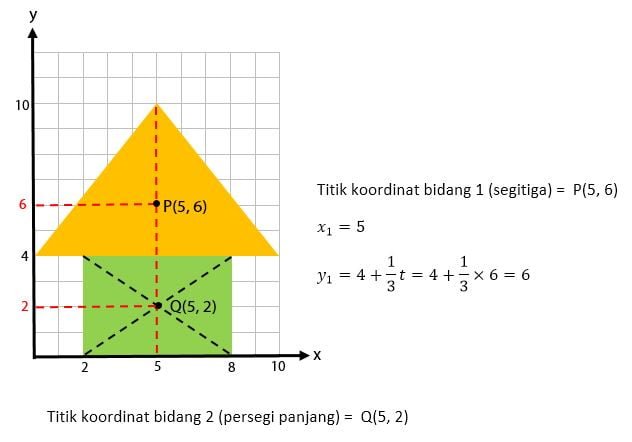
Terlihat bahwa bangun simetri pada titik x = 5, sehingga kondisi ini cukup menguntungkan. Memuat absis titik berat benda adalah x = 5. Sehingga, sobat idschool hanya perlu mencari ordinat titik berat.
Diperoleh koordinat titik berat pada masing – masing bangun adalah P(5, 6) dan Q(5, 2). Selanjutnya adalah mencari koordinat titik berat untuk bangun yang diberikan seperti pada soal.
- Mencari absis titik berat: xo = 5
- Mencari ordinat titik berat yo:
Jadi, koordinat titik berat benda adalah (5; 4,2).
Jawaban: A
Contoh 2 – Soal dan Cara Mencari Titik Berat Benda
Koordinat titik berat bangun luasan seperti gambar di atas terhadap titik O adalah ….
A. 6; 4,70
B. 6; 5,65
C. 6; 6,5
D. 6, 6,71
E. 6; 7,5
Pembahasan:
Dari gambar bangun luasan pada soal dapat diperoleh letak absis dari titik berat bangun (xo) dapat dihitung dari setangah panjang horizontal (sumbu x) dari bangun, yaitu xo = ½ × 12 = 6. Sedangkan absis untuk titik berat bangun luasan dapat dihitung seperti cara berikut.
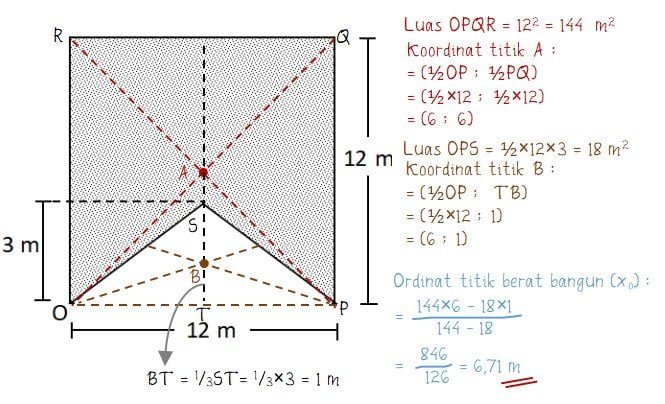
Jadi, Koordinat titik berat bangun luasan seperti gambar di atas terhadap titik O adalah 6; 6,71.
Jawaban: D
Contoh 3 – Soal dan Cara Mencari Titik Berat Benda
Koordinat titik berat bangun luasan gambar di atas terhadap titik O adalah ….
A. 6; 71/5
B. 6; 72/5
C. 6; 81/5
D. 6; 82/5
E. 6; 91/5
Pembahasan:
Benda homogen pada soal mempunyai letak absis untuk titik berat bangun pada xo = ½ × 12 = 6, sedangkan letak ordinat (yo) dapat dihitung dengan rumus titik berat. Sebelumnya perhatikan bahwa bangun berbentuk persegi panjang dengan lubang berbentuk sebuah segitiga di tengah bangun.
- Bangun 1: persegi panjang
Luas bangun: A1 = 18 × 12 = 216
Ordinat titik berat: y1 = ½ × 18 = 9
- Bangun 2: (lubang) segitiga
Luas bangun: A2 = ½ × 12 × 6 = 36
Ordinat titik berat: y2 = 6 + ⅓ × 6 = 6 + 2 = 8
Cara menghitung koordinat titik berat bangun luasan seperti gambar yang diberikan pada soal dapat dihitung seperti pada cara berikut.
Menghitung ordinat titik berat bangun:
yo = A1 · Y1 – A2 · Y2/216 – 36
yo = 216 · 9 – 36 · 8/216 – 36
yo = 1944 – 288/180
yo = 1656/180 = 936/180 = 91/5
Jadi, Koordinat titik berat bangun luasan gambar di atas terhadap titik O adalah 6; 91/5.
Jawaban: E
Contoh 4 – Soal dan Cara Mencari Titik Berat Benda
Perhatikan gambar benda homogen berikut!
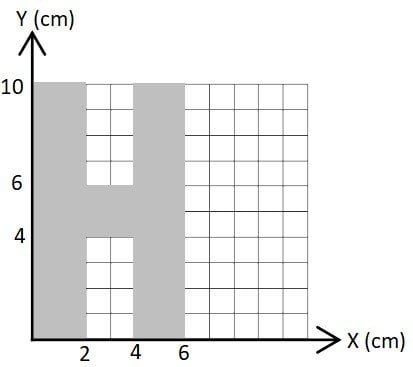
Koordinat titik berat benda homogen tersebut adalah ….
A. 3; 5
B. 3; 5,6
C. 3; 5,8
D. 5,6; 3
E. 5,8; 3
Pembahasan:
Titik berat benda homogen seperti yang diberikan pada soal dapat diperoleh dengan membagi bangun menjadi tiga bagian berupa dua bangun persegi panjang dan sebuah persegi. Dari ketiga titik berat bangun dari setiap bagian, selanjutnya dapat diperoleh koordinat titik berat benda homogen.
Cara mencari titik berat benda homogen seperti pada soal dapat diselesaikan seperti pada pengerjaan berikut.

Jadi, koordinat titik berat benda homogen tersebut adalah 3; 5.
Jawaban: A
Contoh 5 – Soal dan Cara Mencari Titik Berat Benda
Perhatikan bangun karton homogen berikut ini!
Letak koordinat titik berat bangun dari titik A adalah ….
A. 2 cm; 2 cm
B. 21/3 cm; 2 cm
C. 22/3 cm; 2 cm
D. 31/3 cm; 2 cm
E. 22/3 cm; 2 cm
Pembahasan:
Cara menentukan letak koordinat titik berat bangun dari titik A dapat diketahui seperti pada cara penyelesaian di bawah.

Jadi, Letak koordinat titik berat bangun dari titik A adalah 21/3 cm; 2 cm.
Jawaban: B
Demikianlah ulasan materi cara mencari titik berat benda 2 dimensi (luasan) yang dilengkapi dengan contoh soal titik berat benda homogen beserta pembahasannya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.




kalau semisal bangunannya ada beberapa bagian yang diarsir itu nanti pengerjaannya gimana ya ?
Sama ka, tinggal dipisah-pisah bagiannya,kemudian dilanjutkan rumusnya.