Rumus Trigonometri Sudut Rangkap

Dalam materi trigonometri, selain ada rumus jumlah dan selisih dua sudut untuk menghitung nilai suatu sudut yang bukan sudut istimewa terdapat rumus trigonometri sudut rangkap. Seperti halnya rumus jumlah dan selisih dua sudut, rumus sudut rangkap diguanakan untuk menentukan nilai fungsi trigonometri untuk suatu sudut tanpa alat bantu hitung seperti kalkulator atau tabel. Besar sudut yang dicari dengan sudut rangkap pada umumnya bukan merupakan sudut istimewa trigonometri.

Besar sudut yang termasuk dalam sudut istimewa meliputi 30^o, 45^o, 60^o, 90^o, dan beberapa sudut istimewa lainnya. Sedangkan contoh sudut yang bukan merupakan sudut istimewa adalah 75^o, 105^o, dan lain sebagainya. Rumus trigonometri sudut rangkap meliputi 3 persamaan fungsi trigonometri yang meliputi fungsi sin, cos, dan tan sudut rangkap yang sesuai persamaan di bawah.

Bagaimanakah penggunaan dari rumus fungsi trigonometri sudut rangkap? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Tujuan Penggunaan Sudut Rangkap
• Rumus Sudut Rangkap Fungsi Sinus
• Rumus Sudut Rangkap Fungsi Cosinus
• Rumus Sudut Rangkap Fungsi Tangen

Tujuan Penggunaan Sudut Rangkap

Rumus sudut rangkap dapat digunakan untuk mempermudah perhitungan dan meminimalkan hafalan dalam mengingat besar nilai fungsi trigonometri. Sebagai contoh, diketahui bahwa sudut 60^o merupakan sudut istimewa yang sobat idschool ketahui besar nilai fungsinya yaitu sin 60^o = ¹/₂√3 dan cos 60^o = ¹/₂. Melalui rumus sudut rangkap trigonometri, sobat idschool dapat mengetahui nilai fungsi trigonometri untuk sudut 120^o.

Rumus sudut rangkap trigonometri juga dapat digunakan untuk membuktikan fungsi trigonometri lainnya. Selain itu juga dapat digunakan untuk menyelesaikan beberapa permasalahan terkait fungsi trigonometri.

Baca Juga: Rumus Fungsi Trigonometri Sudut Pertengahan

Rumus Sudut Rangkap Fungsi Sinus

Persamaan sudut rangkap untuk fungsi sinus dapat dinyatakan melalui sebuah persamaan, yaitu sin 2 alfa sama dengan 2 dikali sin alfa dikali cos alfa. Rumusnya secaea matematis dinyatakana seperti pada persamaan berikut.

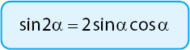
Perhatikan bagaimana pembuktian atau asal-usul persamaan rumus di atas.

Bukti:
sin 2α = sin  (α + α)
sin 2α = sin α × cos α + cos α × sin α
sin 2α = sin α × cos α + sin α × cos α
sin 2α = 2 × sin α × cos α [Terbukti]

Contoh penggunaan:

Soal:
Tentukan nilai dari sin 15^o × cos 15^o!

Pembahasan:
Diketahui bahwa nilai sin 30^o = ¹/₂, nilai sin 15^o × cos 15^o dapat diperoleh seperi yang ditunjukkan cara berikut.

sin 30^o = 2 × sin α × cos α
sin (2 × 15^o) = 2 × sin 15^o × cos 15^o
1/₂ = 2 × sin 15^o × cos 15^o
sin 15^o × cos 15^o = ¹/₂ : 2
sin 15^o × cos 15^o = ¹/₂ × ¹/₂ = ¹/₄

Jadi, nilai dari sin 15^o × cos 15^o = ¹/₄

Rumus Sudut Rangkap Fungsi Cosinus

Ada tiga rumus yang dapat digunakan untuk menentukan nilai sudut rangkap cosinus. Ketiga rumus tersebut secara matematis dinyatakan seperti pada persamaan berikut.

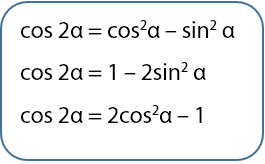
Bukti persamaan 1:
cos 2α = cos(α + α)
cos 2α = cos α × cos α – sin α × sin α
cos 2α = cos²α – sin²α

Selanjutnya akan dibuktikan bahwa persamaan kedua dan ketiga adalah persamaan yang benar. Sebelum membuktikan kedua rumus lainnya, ingat kembali rumus identitas trigonometri dari persamaan sin²α + cos²α = 1.

Bukti persamaan kedua:
cos 2α = cos²α – sin²α
cos 2α = (1 – sin²α) – sin²α
cos 2α = 1 – sin²α – sin²α
cos 2α = 1 – 2×sin²α

Bukti persamaan ketiga:
cos 2α = cos²α – sin²α
cos 2α = cos²α – (1 – cos²α)
cos 2α = cos²α – 1 + cos²α
cos 2α = cos²α + cos²α – 1
cos 2α = 2 cos²α – 1

[Terbukti] benar untuk ketiga persamaan.

Contoh penggunaan:

Soal:
Tentukan nilai fungsi cosinus untuk sudut 120^o dengan memanfaatkan rumus pada sudut rangkap!

Pembahasan:
cos 120^o = cos ( 2 × 60^o)
cos 120^o = cos²60^o – sin²60^o
cos 120^o = (¹/₂)² – (¹/₂√3)²
cos 120^o = ¹/₄ – ³/₄ = –²/₄
cos 120^o = –²/₄
cos 120^o = –¹/₂

Baca Juga: Fungsi Trigonometri dan Sudut Istimewa pada Trigonometri

Rumus Sudut Rangkap Fungsi Tangen

Terdapat sebuah persamaan yang menyatakan persamaan sudut rangkap fungsi tangen yang dinyatakan seperti rumus berikut.

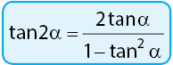
Dari mana persamaan di atas diperoleh? perhatikan pembuktian berikut.

Bukti:
tan 2α = tan(α + α)
tan 2α = ^{tan α + tan α}/1 – tan α × tan α
tan 2α = ^{2 tan α}/_1– tan2α [Terbukti]

 Contoh penggunaan::

Jika diketahui nilai tan α = ²/₃ dan sudut α merupakan sudut lancip maka tentukan nilai tan 2α!

Pembahasan:

Sekian pembahasan mengenai rumus trigonometri sudut rangkap untuk fungsi sinus, cosinus, dan rumus tangen. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Rumus Jumlah dan Selisih Dua Sudut