Sifat-sifat Komposisi Fungsi

Komposisi fungsi adalah kombinasi dari dua fungsi sehingga menjadi sebuah fungsi baru yang merupakan gabungan dari kedua fungsi. Simbol komposisi dari dua fungsi dihubungkan dengan tanda o yang biasa disebut/dibaca dengan bundaran.

Misalnya sebuah fungsi h(x) merupakan penggabungan dari fungsi f(x) yang dilanjutkan dengan fungsi g(x). Persamaan fungsi h(x) sama dengan f(g(x)) = (f o g)(x), dengan (f o g)(x) dibaca f bundaran g(x). Cara menentukan persamaan fungsi h(x) dengan melakukan operasi (f o g)(x) yang merupakan suatu komposisi fungsi.

Bagaiman cara menentukan hasil komposisi fungsi? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Pengertian Komposisi Fungsi
• Sifat-sifat Komposisi Fungsi
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Komposisi Fungsi
  • Contoh 2 – Soal Fungsi Komposisi
  • Contoh 3 – Soal Komposisi Fungsi

Pengertian Komposisi Fungsi

Sebuah fungsi h(x) = (f o g) (x) artinya persamaan h(x) sama dengan fungsi dengan persamaan f(x) kemudian dilanjut dengan g(x). Kondisi ini memberikan hasil dari daerah asal dengan fungsi f(x) yang dilanjut dengan fungsi g(x) akan sama dengan melalui fungsi h(x) secara langsung. Gambar yang menunjukkan antara fungsi f dan g dengan fungsi h dapat dilihat seperti berikut.

 
Proses pertama (tanda panah bagian atas) adalah fungsi f memetakan himpunan pertama ke himpunan ke dua dilanjutkan pemetaan ke himpunan ke tiga. Sedangkan pada proses ke dua (tanda panah bagian bawah), pemetaan h memetakan anggota himpunan pertama langsung ke himpunan ke tiga.

Proses penggabungan fungsi f dan fungsi g inilah yang disebut dengan komposisi fungsi, di mana hasilnya merupakan pemataan langsung oleh fungsi h.

Baca Juga: Komposisi Transformasi Geometri dengan Matriks 

Sifat-sifat Komposisi Fungsi

Ada tiga sifat pada komposisi fungsi yaitu tidak komutatif, asosiatif, dan memiliki elemen identitas. Sifat-sifat komposisi dari dua fungsi dapat memudahkan kita untuk menyelesaikan masalah terkait komposisi fungsi dengan tepat. Berikut ini adalah ketiga sifat fungsi komposisi dalam bentuk persamaan matematis.
 

Baca Juga: Cara Menentukan f(x) jika Diketahui (f ∘ g)(x) atau (g ∘ f)(x)

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Komposisi Fungsi

Diketahui f(x) = x² + 4x dan g(x) = –2 + √(x + 4) dengan x ≠ –4 dan x E∊ R. Fungsi komposisi (g o f)(x) adalah ….
A. 2x – 4
B. x – 2
C. x + 4
D. x
E. 2x

Pembahasan:

(g o f) (x) = g(f(x))
= g(x² + 4x)
= –2 +√(x² + 4x + 4)

Faktorkan persamaan kuadrat yang berada dalam tanda akar sehingga diperoleh hasil berikut.

(g o f)(x) = –2 + √[(x+2)²]
(g o f)(x) = –2 + (x+2) = –2 + x + 2 = x

Jadi, fungsi komposisi (g o f)(x) adalah x.

Jawaban: D

Contoh 2 – Soal Fungsi Komposisi

Pembahasan:

Jawaban: C
 
Baca Juga: Relasi dan Fungsi: Pengertian, Perbedaan, dan Contoh Soal

Contoh 3 – Soal Komposisi Fungsi

Diketahui fungsi g(x) = 2x – 1 dan persamaan (f o g)(x) = 4x² + 2x + 2. Maka nilai f(x) adalah ….
A. x² – 3x + 4
B. x² + 3x – 4
C. x² – 3x – 4
D. x² + 3x + 4
E. x² + 3x – 2

Pembahasan:

Diketahui: (f o g)(x) = 4x² + 2x + 2
Sehingga f(2x–1) = 4×2 + 2x + 2

Misalkan a = 2x – 1, maka:

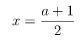
 Selanjutnya, substitusi a dan x hasil pemisalan di atas seperti cara di bawah.

Jadi, nilai f(x) adalah x² + 3x + 4.

Jawaban: D

Sekian Pembahasan mengenai komposisi fungsi disertai sifat-sifatnya dan contoh soal komposisi fungsi beserta pembahasan. Jika ada pertanyaan bisa tinggalkan pada kolom komentar di bawah. Terimakasih telah mengunjungi idschool.net, semoga bermanfaat.

 
Baca Juga: Fungsi Invers dan Sifat Fungsi Invers pada Komposisi Fungsi