Relasi dan Fungsi: Pengertian, Perbedaan, dan Contoh Soal

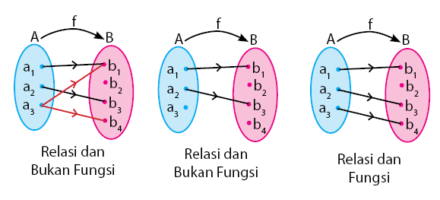
Arti sederhana dari relasi dapat diartikan sebagai hubungan, sedangkan fungsi merupakan hubungan yang memiliki suatu syarat tertentu. Sehingga dapat dikatakan bahwa antara relasi dan fungsi adalah dua jenis hubungan yang berbeda. Hubungan yang dimaksud di sini adalah hubungan antara daerah asal (domain) dan daerah kawan (kodomain). Setiap fungsi termasuk dalam relasi, namun setiap relasi belum tentu merupakan fungsi. Perbedaan antara relasi dan fungsi terletak pada cara memasangkan anggota himpunan ke daerah asalnya.

Pada relasi, tidak ada aturan khusus untuk memasangkan setiap anggota himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas pernyataan relasi tersebut. Setiap anggota himpunan daerah asal boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan. Sedangkan pada fungsi, setiap anggota himpunan daerah asal dipasangkan dengan aturan khusus. Aturan tersebut mengharuskan setiap anggota himpunan daerah asal mempunyai pasangan dan hanya tepat satu dipasangkan dengan daerah kawannya.

Baca Juga: Perbandingan Senilai dan Berbalik Nilai

Bagaimana pengertian dari relasi dan fungsi? Bagaimana cara mengenali relasi dan fungsi? Sobat idschool dapat mencari tahu jawabannya melalui ulasan pengertian/perbedaan dari relasi dan fungsi seperti berikut.

Table of Contents

• Daerah Asal, Kawan, dan Hasil
• Relasi
• Fungsi atau Pemetaan
• Sifat-sifat Fungsi
  • 1. Fungsi Injektif/Fungsi Satu-Satu (Fungsi Into)
  • 2. Fungsi Surjektif (Fungsi Onto)
  • 3. Fungsi Bijektif (Korespondensi Satu-Satu)

Daerah Asal, Kawan, dan Hasil

Dalam pembahasan relasi dan fungsi, himpunan yang terlibat digolongkan ke dalam tiga jenis daerah. Ketiga daerah tersebut adalah daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range). Secara umum, himpunan ketiga daerah tersebut dapat dilihat pada gambar di bawah.

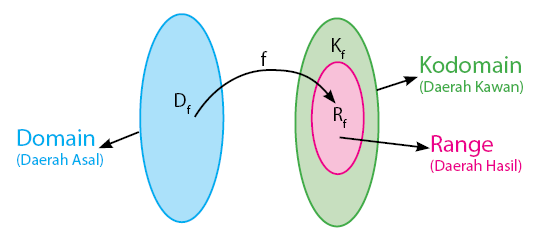
Definisi dari ketiga daerah tersebut diberikan seperti berikut.

• Domain (daerah asal): himpunan tidak kosong di mana anggota sebuah relasi didefinisikan.
• Kodomain (daerah kawan): himpunan tidak kosong dimana anggota domain memiliki pasangan sesuai relasi yang didefinisikan.
• Range (daerah hasil): semua anggota kodomain yang memiliki pasangan pada anggota domain.

Baca Juga: Cara Menentukan Domain, Kodomain, dan Range

Relasi

Seperti yang telah dijelaskan secara singkat di atas, relasi dapat diartikan sebagai hubungan. Misalkan sebuah relasi menyatakan hubungan perkalian. Hasil relasi tersebut dapat dinyatakan dalam himpunan pasangan terurut x dan y dan dapat juga digambar pada bidang kartesius.

Cara menyatakan hasil relasi perkalian antara himpunan A dan B dapat dilihat pada contoh permasalahan di bawah.
A = { 1, 2, 3 }
B = { 2, 3 }
A × B = {1, 4, 6, 3, 6, 9}

Sebuah relasi menyatakan pemetaan dengan fungsi f(x) merupakan perkalian A dan B. Anggota himpunan x adalah semua anggota A dan anggota himpunan y atau f(x) adalah hasil perkalian anggota A dan B.

x = {1, 2, 3}
y = {1, 4, 6, 3, 6, 9}

Gambar di bawah menyatakan relasi dalam bidang kartesius.

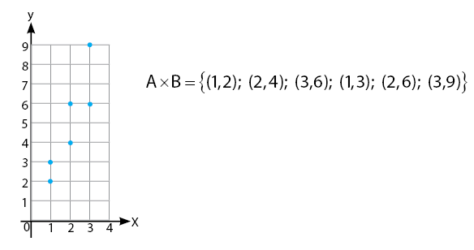
Baca Juga: Sifat-sifat dan Contoh Soal Komposisi Fungsi

Fungsi atau Pemetaan

Fungsi adalah relasi yang memasangkan setiap anggota himpunan daerah asal tepat satu ke himpunan daerah kawannya. Fungsi sering disebut juga dengan pemetaan termasuk dalam himpunan relasi. Suatu relasi disebut fungsi jika semua anggota himpunan daerah asal dipasangkan tepat satu ke daerah kawannya. Simbol fungsi yang memetakan himpunan A ke B adalah f: A → B.

Contoh permasalahan pada fungsi, diketahui himpunan A dan B diberikan seperti di bawah.
A = { 0, 1, 2, 3, 4 }
B = { 0, 1, 2, …, 10}
Didefinisikan fungsi f: A → B dengan f(x) = x + 5.
Tentukan hasil pemetaan dari x ∈ A oleh fungsi f, D_f, K_f, dan R_f!

Pembahasan:
Peta dari x ∈ A oleh fungsi f yaitu y = f(x) = x + 5:

• f(0) = 0 + 5 = 5
• f(1) = 1 + 5 = 6
• f(2) = 2 + 5 = 7
• f(3) = 3 + 5 = 8
• f(4) = 4 + 5 = 9

Hasil dari perhitungan f(x) di atas merupakan daerah hasil/range. Daerah asal/domain adalah semua anggota himpunan A. Sedangkan daerah kawan/kodomain adalah semua anggota B.  

• Daerah asal (domain): D_f = A = { 0, 1, 2, 3, 4 } 
• Daerah kawan (kodomain): K_f = B = { 0, 1, 2, …, 10} 
• Daerah hasil (range) = R_f = {5, 6, 7, 8, 9}

Baca Juga: Contoh Persaamaan Matematika yang Merupakan Fungsi

Sifat-sifat Fungsi

Fungsi dikelompokkan menjadi 3 (tiga) jenis yaitu fungsi Injektif, Surjektif, dan Bijektif. Pengelompokkan tersebut didasarkan pada sifatnya. Perbedaan ketiga jenis tersebut dapat disimak pada penjelasan di bawah.

1. Fungsi Injektif/Fungsi Satu-Satu (Fungsi Into)

Fungsi pertama yang akan dibahas adalah fungsi injektif atau sering disebut dengan fungsi into atau fungsi satu-satu. Fungsi f: A → B dikatakan fungsi injektif jika dan hanya jika anggota kodomain hanya dipasangkan satu kali dengan anggota domain. Pada fungsi injektif, anggota himpunan daerah kodomain boleh tidak memiliki pasangan, namun semua anggota kodomain yang terpasangkan hanya ada satu, tidak boleh ada yang lebih dari satu.

Perhatikan gambar di bawah untuk melihat lebih detail mengenai perbedaannya.

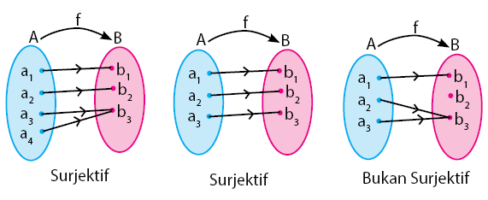
2. Fungsi Surjektif (Fungsi Onto)

Fungsi Surjektif atau onto memiliki ciri yaitu anggota kodomainnya boleh memiliki pasangan lebih dari satu, namun tidak boleh ada anggota kodomain yang tidak dipasangkan. Fungsi surjektif biasanya dipenuhi apabila jumlah anggota kodomain sama atau lebih sedikit dari anggota domain.

Perhatikan gambar di bawah untuk menambah pemahaman sobat idschool tentang sifat fungsi surjektif.

3. Fungsi Bijektif (Korespondensi Satu-Satu)

Fungsi Bijektif merupakan gabungan dari fungsi injektif dan surjektif. Pada fungsi bijektif, semua anggota domain dan kodomain terpasangkan tepat satu. Kebalikan fungsi dari fungsi injektif dan surjektif belum pasti fungsi/pemetaan, namun kebalikan fungsi dari fungsi bijektif juga merupakan fungsi/pemetaan.

Pemetaan bijektif terlihat seperti gambar di bawah.

Terlihat bahwa kebalikan dari fungsi f juga merupakan fungsi atau pemetaan, bukan?

Sekian pembahasan mengenai relasi dan fungsi, serta perbedaan dan contoh soal. Jika ada bagian yang kurang paham mengenai ulasan relasi dan fungsi di atas, sobat idschool dapat menanyakannya pada kolom komentar di bawah. Terimakasih sudah mengunjungi ulasan relasi dan fungsi dari idschool.net, semoga bermanfaat.

Baca Juga: Fungsi Invers dan Sifat Fungsi Invers pada Komposisi Fungsi