Cara Menentukan Banyaknya Anggota Himpunan Bagian

Cara menentukan banyaknya anggota himpunan bagian dari sebuah himpunan yang memiliki n anggota adalah menggunakan rumus 2ⁿ. Sebagai contoh sebuah himpunan A memiliki 3 anggota maka banyaknya himpunan bagian dari himpunan A akan sama dengan 2³ = 8. Misalkan himpunan A = {a, b c}, himpunan bagian A = {(); (a); (b); (c); (a, b); (a, c); (b, c); (a, b, c)} ada sebanyak 8.

Himpunan A = {a, b, c} memiliki anggota himpunan bagian yang terdiri dari 3 anggota sebanyak 1 yaitu (a, b, c). Banyak anggota himpunan bagian yang terdiri dari 2 anggota ada sebanyak tiga yaitu (a, b); (a, c); dan (b, c). Sementara banyak anggota himpunan bagian yang memiliki 1 anggota juga ada sebanyak tiga yaitu (a); (b); dan (c). Himpunan kosong akan selalu menjadi anggota himpunan bagian dari setiap himpunan yang jumlahnya ada 1.

Cara menentukan banyaknya anggota himpunan bagian yang terdiri dari 1, 2, …, dan n anggota dapat secara mudah diperoleh dengan segitiga pascal. Apa itu himpunan? Bagaimana cara menentukan banyaknya anggota himpunan yang terdiri dari 2 anggota? Bagaimana cara menentukan banyaknya anggota himpunan yang terdiri dari 3 anggota atau banyak anggota lainnya?

Sobat idschool dapat mencari tahu jawaban bagaimana cara menentukan banyaknya anggota himpunan bagian melalui ulasan di bawah.

Table of Contents

• Apa Itu Himpunan?
• Himpunan Bagian
• Rumus dan Cara Menentukan Banyaknya Anggota Himpunan Bagian
• Contoh Soal dan Pembahasan
  • Contoh 1 – Cara Menentukan Banyaknya Anggota Himpunan Bagian
  • Contoh 2 – Cara Menentukan Banyaknya Anggota Himpunan Bagian

Apa Itu Himpunan?

Himpunan adalah kumpulan objek-objek yang berbeda yang disebut elemen, unsur, atau anggota. Suatu himpunan memiliki syarat keanggotaan yang terdefinisi dengan jelas. Contohnya adalah himpunan hewan berkaki empat. Dalam himpunan yang telah didefinisikan tersebut dapat meliputi kambing, sapi, kerbau, singa, harimau, dan hewan berkaki empat lainnya.

Contoh himpunan lainnya adalah himpunan 5 bilangan prima pertama. Himpunan tersebut jelas terdefinisi untuk anggota himpunan yang terdiri dari bilangan 2, 3, 5, 7, dan 11.

Jika syarat keanggotaan tidak terdefinisi dengan jelas maka tidak bisa disebut dengan himpunan. Contoh sebuah definisi yang bukan himpunan adalah himpunan perempuan cantik di Jakarta. Definisi cantik merupakan kata sifat yang tidak jelas, sehingga perempuan cantik tidak dapat menjadi contoh himpunan.

Sebuah himpunan dinyatakan dengan menggunakan kurung kurawal { } dan diberi nama dengan huruf kapital. Sedangkan anggota himpunan dituliskan di dalam tanda kurung kurawal menggunakan huruf kecil.

Contohnya adalah himpunan A dengan anggota huruf vokal, untuk menyatakan himpunan A dapat dituliskan dengan mendaftar anggota-anggota himpunan A yaitu A = {a, i, u, e, o}.

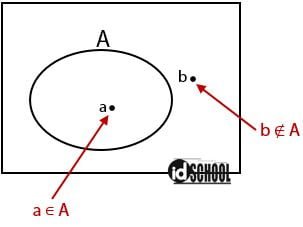
Notasi untuk menyatakan sebuah anggota merupakan bagian dari suatu himpunan adalah ∊. Misalkan terdapat sebuah himpunan A dan a merupakan anggota dari A dan b bukan merupakan anggota dari a. Untuk menyatakan kalimat tersebut dalam notasi himpunan adalah a ∊ A. Sedangkan untuk menyatakan b yang bukan anggota himpunan A adalah b ∉ A.

Baca Juga: Himpunan dan Diagram Venn

Himpunan Bagian

Sebuah himpunan memuat himpunan bagian yang terdiri dari anggota-anggota himpunan dengan banyak anggota sama dengan kosong, satu, dua, sampai n anggota. Himpunan bagian atau subset adalah suatu himpunan yang termuat dalam himpunan lain yang cakupannya lebih luas. Simbol himpunan bagian dinyatakan dalam notasi ⊂ atau ⊆.

Himpunan A merupakan himpunan bagian B bila himpunan A termuat di dalam B. Notasi untuk menyatakan himpunan A adalah subset atau himpunan bagian dari (atau termasuk ke dalam) B adalah A ⊂ B atau A ⊆ B.

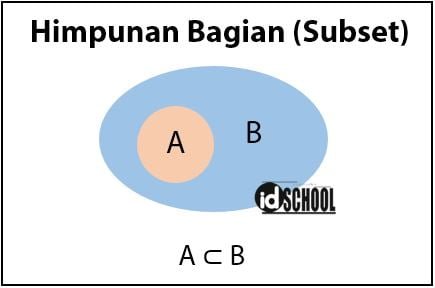
A ⊂ B berbeda dengan A ⊆ B. Pada A ⊂ B memiliki pengertian A dalah himpunan bagian dari B tetapi A ≠ B. Sedangkan A ⊆ B memiliki pengertian bahwa A adalah himpunan bagian/subset dari B yang memungkinkan A = B.

Dua buah himpunan A dan B dapat memenuhi A = B jika dan jika setiap anggota A merupakan anggota B dan anggota B merupakan anggota A. Dengan kata lain, pernyataan tersebut sama dengan A = B jika A adalah himpunan bagian dari B dan B adalah himpunan bagian dari A. Selain kondisi tersebut maka A ≠ B.

Setiap himpunan selalu mempunyai himpunan kosong dan himpunan yang persis sama dengan himpunan itu sendiri sebagai himpunan bagiannya. Himpunan bagian juga memuat kombinasi anggota-anggotanya yang banyaknya adalah 1, 2, …, (n – 1) anggota.

Sebagai contoh, sebuah himpunan H memiliki anggota himpunan lima bilangan prima pertama. Diketahui bahwa H = {2, 3, 5, 7, 11}, himpunan tersebut memiliki anggota himpunan bagian sebanyak 32 yaitu {{ }, {2}, {3}, {5}, {7}, {11}, {2, 3}, {2, 5}, {2, 7}, {2, 11}, {3, 5}, {3, 7}, {3, 11}, {5, 7}, {5, 11}, {7, 11}, {2, 3, 5}, {2, 3, 7}, {2, 3, 11}, {2, 5, 7}, {2, 5, 11}, {2, 7, 11}, {3, 5, 7}, {3, 5, 11}, {3, 7, 11}, {5, 7, 11}, {2, 3, 5, 7}, {2, 3, 5, 11}, {3, 5, 7, 11}, {2, 5, 7, 11}, {2, 3, 7, 11}, {2, 3, 5, 7, 11} }.

Cara menentukan banyaknya anggota himpunan bagian dengan cara mendaftar seperti di atas tentu tidak efisien. Sehingga diperlukan cara menentukan banyaknya anggota himpunan bagian yang lebih praktis dan efisien.

Baca Juga: Menentukan Daerah Asal (Domain), Daerah Kawan (Kodomain), dan Daerah Hasil (Range)

Rumus dan Cara Menentukan Banyaknya Anggota Himpunan Bagian

Cara menentukan banyaknya anggota himpunan bagian dapat menggunakan rumus 2ⁿ. Contoh penggunanya, ingat kembali himpunan H yang dijadikan contoh sebelumnya yaitu H = {2, 3, 5, 7, 11} yang memiliki banyak anggota himpunan bagian sebanyak 32.

Himpunan H terdiri dari n(H) = 5 anggota, cara menentukan banyaknya anggota himpunan bagian dari himpunan H dapat diperoleh menggunakan perhitungan = 2^n(H) = 2⁵ = 32.

Secara umum untuk sebuah himpunan dengan n anggota, cara menentukan banyaknya anggota himpunan bagian dapat diketahui melalui rumus 2ⁿ.

Banyaknya himpunan bagian untuk himpunan H yang terdiri dari 1, 2, 3, 4, dan 5 anggota diberikan seperti daftar berikut.

• Anggora himpunan bagian H berupa himpunan kosong ada sebanyak 1, yaitu himpunan kosong { }
• Anggota himpunan H dengan 1 anggota ada sebanyak 5 yaitu {{2}, {3}, {5}, {7}, {11}}
• Anggota himpunan bagian H dengan 2 anggota ada sebanyak 10: {{2, 3}, {2, 5}, {2, 7}, {2, 11}, {3, 5}, {3, 7}, {3, 11}, {5, 7}, {5, 11}, {7, 11}}
• Anggota himpunan bagian H dengan 3 anggota ada sebanyak 10: {{2, 3, 5}, {2, 3, 7}, {2, 3, 11}, {2, 5, 7}, {2, 5, 11}, {2, 7, 11}, {3, 5, 7}, {3, 5, 11}, {3, 7, 11}, {5, 7, 11}}
• Anggota himpunan bagian H dengan 4 anggota ada sebanyak 5: {{2, 3, 5, 7}, {2, 3, 5, 11}, {3, 5, 7, 11}, {2, 5, 7, 11}, {2, 3, 7, 11}}
• Anggota himpunan bagian H dengan 5 anggota ada sebanyak 1: {(2, 3, 5, 7, 11)}

Cara menentukan banyaknya anggota himpunan bagian yang terdiri dari 1, 2, 3, …, sampai n anggota dengan mendaftar seperti di atas tentu tidak praktis. Ada cara lain yang dapat digunakan sebagai cara menentukan banyaknya anggota himpunan bagian yang terdiri dari x anggota dengan menggunakan segitiga pascal.

Sebagai contoh gunakan kembali himpunan H yang terdiri dari 5 anggota yaitu H = {2, 3, 5, 7, 11}.

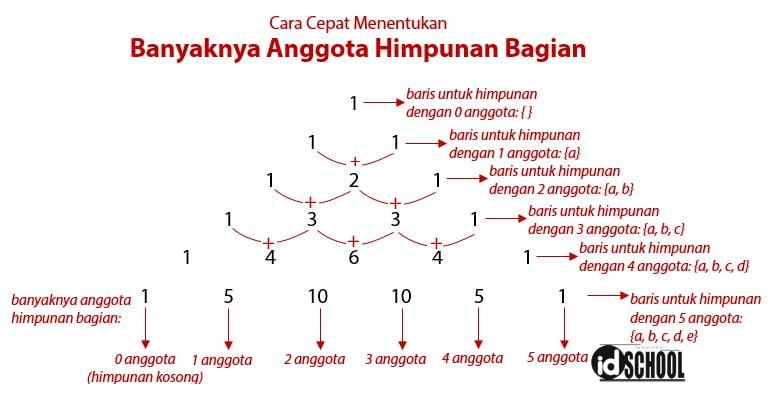
Dari segitiga pascal dapat diperoleh cara menentukan banyaknya aggota himpunan bagian yang terdiri dari 0, 1, 2, 3, 4, dan 5 anggota untuk himpunan H berturut-turtut adalah 1, 5, 10, 10, 5, dan 1. Bilangan-bilangan ini sesuai dengan banyaknya anggota himpunan bagian H yang terdiri dari 0, 1, 2, 3, 4, dan 5 anggota dengan cara mendaftarnya.

Baca Juga: Cara Menentukan Banyaknya Pemetaan

Contoh Soal dan Pembahasan

Sobat idschool dapat melatih kemampuan pemahaman materi himpunan bagian pada beberapa contoh soal di bawah. Contoh soal yang diberikan sudah dilengkapi dengan pembahasan bagaimana cara menentukan banyaknya anggota himpunan bagian. Gunakan pembahasan soal sebagai tolak ukur keberhasilan soobat idschool dalam memahai cara menentukan banyaknya anggota himpunan bagian. Selamat Berlatih!

Contoh 1 – Cara Menentukan Banyaknya Anggota Himpunan Bagian

P = {x | x ≤ 13, x ∊ bilangan prima}
Banyaknya himpunan bagian dari P yang mempunyai 2 anggota adalah ….
A.   25
B.   15
C.   12
D.   7

Pembahsan:
Dari soal diektahui bahwa:
P = {x | x ≤ 13, x ∊ bilangan prima}
P = {2, 3, 5, 7, 11, 13} → himpunan dengan 6 anggota

Segitiga pascal untuk himpunan dengan 6 anggota:

                    1
               1        1
            1      2      1
         1    3       3      1
      1    4      6      4     1
   1   5    10    10     5   1
1   6   15    20     15    6  1

Berdasarkan segitiga pascal di atas, banyak himpunan bagian dari P untuk 0, 1, 2, 3, 4, 5, dan 6 anggota berturut – turut adalah 1, 6, 15, 20, 15, 15, 6, dan 1.

Jadi, banyaknya himpunan bagian dari P yang mempunyai 2 anggota adalah 15.

Jawaban: B

Contoh 2 – Cara Menentukan Banyaknya Anggota Himpunan Bagian

Jika T = {y | 20 < y < 30, y ∊ himpunan bilangan prima}, banyak himpunan bagian dari T adalah ….
A.   16
B.   8
C.   4
D.   2

Pembahasan:
T = {y | 20 < y < 30, y ∊ himpunan bilangan prima}
T = {23, 29} → banyaknya anggota: n = 2

Banyaknya anggota himpunan bagian dengan sebuah himpunan yang terdiri dari n anggota dapat dihitung menggunakan rumus 2ⁿ.

Jadi, banyaknya himpunan bagian dari T adalah 2² = 4.

Jawaban: C

Demikianlan ulasan materi cara menentukan banyaknya anggota himpunan bagian dengan x anggota dari n anggota. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Kalimat Terbuka dan Tertutup dalam Matematika