Unsur-unsur lingkaran tidak hanya memuat jari-jari dan pusat lingkaran, namun memuat juga busur, juring, dan tembereng. Busur lingkaran adalah bagian dari keliling lingkaran, di mana panjang busur lingkaran dapat dihitung berdasarkan besar sudut yang menghadap busur dan keliling lingkaran. Sedangkan luas juring lingkaran adalah bagian dari luas lingkaran yang luasnya dipengaruhi oleh besar sudut dan luas lingkaran.
Panjang busur berhubungan dengan keliling lingkaran, sedangkan luas juring berkaitan dengan luas lingkaran. Sedagkan luas tembereng melibatkan perhitungan luas lingkaran dan luas segitiga. Bagaimana cara menghitung panjang busur lingkaran? Bagaimana cara menghitung luas juring dan tembereng lingkaran? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Panjang Busur Lingkaran
Panjang busur merupakan bagian dari keliling lingkaran yang dibatasi oleh dua titik. Kedua titik tersebut dan pusat lingkaran membentuk sebuah sudut. Bagian busur yang akan dimaksud dapat dilihat dari gambar berikut.
Baca Juga: Sudut Pusat dan Sudut Keliling Lingkaran
Rumus Mencari Panjang Busur AB
Panjang busur lingkaran bergantung dari besar sudut yang dibentuk oleh dua titik ujung busur lingkaran dan pusat lingkaran. Misalkan sebuah panjang busur lingkaran dihubungkan oleh titik A dan titik B, Besar sudut yang dibatasi oleh titik A, pusat lingkaran O, dan titik B adalah ∠AOB.
Hubungan panjang busur lingkaran dan besar ∠AOB dinyatakan melalui persamaan di bawah.
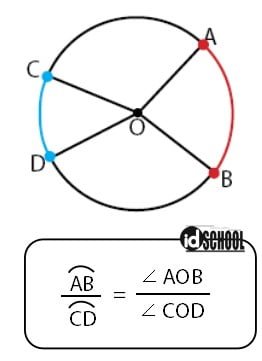
Jika pada sebuah lingkaran terdapat dua panjang busur yang sama maka kedua panjang busur lingkaran dapat dinyatakan dalam sebuah hubungan. Misalhan busur AB dan busur CD terdapat pada sebuah lingkaran O, hubungan kedua panjang busur lingkaran dinyatakan melalui persamaan berikut.
Baca Juga: Kesebangunan Trapesium
Contoh Soal Mencari Panjang Busur Lingkaran dan Pembahasan
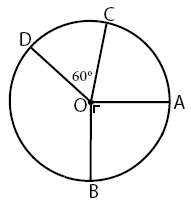
Perhatikan gambar di bawah!
Jika panjang busur AB adalah 32 cm maka panjang busur CD adalah ….
A. 211/3 cm
B. 212/3 cm
C. 221/3 cm
D. 222/3 cm
Pembahasan:
Berdasarkan keterangan pada soal, dapat diketahui bahwa:
1) besar ∠AOB = 90o (siku-siku)
2) besar ∠COD = 60o
3) panjang busur AB = 32 cm
Menghitung panjang busur CD:

Kalikan silang, sehingga diperoleh panjang busur CD:
3CD = 32 × 2
3CD = 64
CD = 64/3 = 211/3 cm
Jadi, panjang busur CD adalah 211/3 cm.
Jawaban: A
Luas Juring
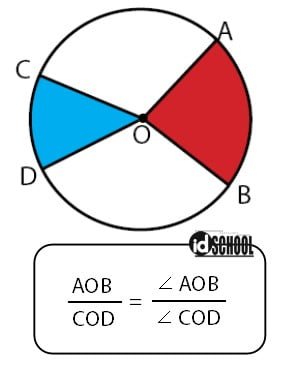
Juring merupakan daerah yang dibatasi oleh dua jari-jari dan satu busur. Daerah yang dibatasi tersebut merupakan bagian dari luas lingkaran. Bagian juring lingkaran pada sebuah lingkaran ditunjukkan seperti gambar berikut.
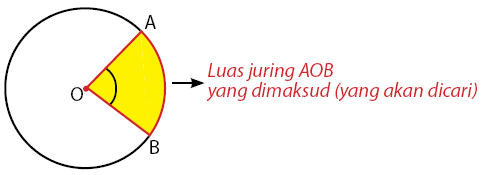
Rumus Luas Juring AOB
Sebuah juring lingkaran dibatasi oleh titik A dan titik B pada tepi lingkaran O. Besar sudut yang dibentuk titik A, pusat lingkaran O, dan titik B adalah ∠AOB . Besar juring lingkaran AOB dapat dihiting melalui persamaan di bawah.
Jika pada sebuah lingkaran terdapat dua buah jurin lingkaran maka kedua luas juring dapat dinyatakan dalam sebuah persamaan. Hubungan antara dua luas juring dengan besat sudut pusat yang berbeda dinyatakan melalui persamaan di bawah.
Baca Juga: Sistem Persamaan Linear Dua Variabel (SPLDV)
Contoh Soal Luas Juring dan Pembahasan
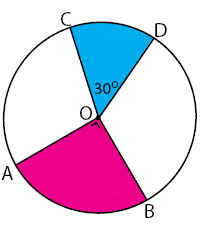
Perhatikan gambar berikut!
Lingkaran di atas memiliki ukuran jari-jari sebesar 10,5 cm. Luas juring COD adalah ….
A. 28,875 cm2
B. 288,75 cm2
C. 2.887,5 cm2
D. 28.875 cm2
Pembahasan:
Berdasarkan keterangan pada gambar, kita dapat mengetahui bahwa besar sudut AOB adalah 90 o. Luas juring AOB dapat dihitung seperti cara berikut.

Selanjutnya, kita akan mencari luas juring COD:

Jawaban: A
Luas Tembereng
Tembereng merupakan daerah yang dibatasi oleh sebuah tali busur dan busur. Luas tembereng diperoleh dengan cara mengurangkan luas juring dengan luas segitiga. Misalkann dua titik A dan titik B terletak pada sebuah lingkaran sehingga terbentuk juring AOB. Jika titik A, tiitk B, dan titik pusat lingkaran O dihubungkan garis lurus maka terdapat sebuah segitiga AOB. Bagian di dalam juring AOB dan di luar segitiga AOB merupakan daerah yang disebut tembereng.

Luas tembereng dapat dihitung melalui luas juring dikurang luas segitiga AOB.
Luas tembereng = Luas juring AOB – Luas segitigan AOB
Contoh Soal Luas Pembereng dan Pembahasan
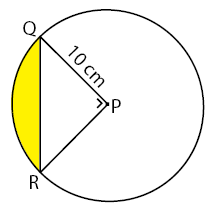
Perhatikan gambar berikut!
Luas daerah yang diarsir pada gambar di atas adalah …. (π = 3,14)
A. 78,5 cm2
B. 50 cm2
C. 38 cm2
D. 28,5 cm2
Pembahasan:
Daerah yang diarsir merupakan tembereng. Luas tembereng dapat dihitung dengan mengurangkan luas juring PQR dengan luas segitia PQR. Sehingga kita perlu menghitung luas juring PQR dengan luas segitia PQR terlebih dahulu. Kemudian kita bisa mendapatakan luas tembereng.
Luas Juring PQR:
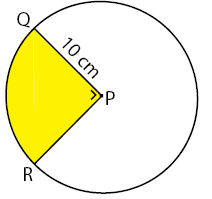
Berdasarkan pada gambar di atas dapat diperoleh data bahwa besar ∠PQR = 90o (siku-siku) dan r = 10 cm. Sehingga luas juring PQR dapat dihitung seperti padpa cara berikut.
Menghitung luas juring PQR:
Ljuring PQR = 90/360 × Llingkaran
= 1/4 × (π × r2)
= 1/4 × (3,14 × 102)
= 1/4 × 314
= 78,5 cm2
Luas segitiga PQR:
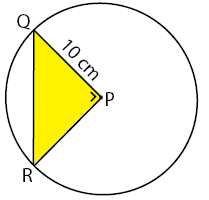
Segitiga PQR merupakan segitiga segitiga sama sisi dan siku-siku di P. PQ = PR = jari-jari =10 cm. Sehingga, luas segitiga PQR dapat dihitung seperti berikut.
Menghitung luas segitiga PQR:
LΔPQR = 1/2 × 10 × 10
= 1/2 × 100
= 50 cm2
Menghitung luas tembereng:
Larsir = Ltembereng
= Ljuring PQR − LΔPQR
= 78,5 − 50 = 28,5 cm2
Jadi, luas daerah yang diarsir sama dengan luas tembereng sama dengan 28,5 cm2.
Jawaban: D
Sekian pembahasan mengenai luas juring dan panjang busur lingkaran, serta luas tembereng dalam lingkaran. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Segi Empat Tali Busur dan Sdutu Antara Dua Tali Busur



bgs bngt mudah dipahami