Sudut pusat lingkaran adalah sudut yang titik sudutnya berada pada pusat lingkaran. Sedangkan sudut keliling lingkaran adalah sudut yang titik sudutnya terdapat pada busur lingkaran. Besar sudut pusat linkgkaran sama dengan dua kali sudut keliling lingkaran yang menghadap busur yang sama.
Busur lingkaran adalah bagian lengkung lingkaran. Perlu diperhatikan bahwa sudut pusat dan sudut keliling lingkaran menghadap busur yang sama. Agar, rumus sudut pusat = 2 × sudut keliling lingkaran dapat digunakan.
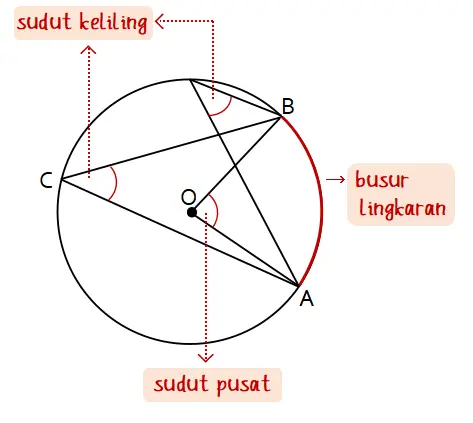
Lebih lanjut mengenai sudut pusat dan sudut keliling lingkaran ada di bawah.
Daftar isi:
- Sudut Pusat Lingkaran
- Sudut Keliling Lingkaran
- Besar Sudut Pusat dan Sudut Keliling Lingkaran
- Contoh Soal dan Pembahasan
Baca Juga: Lingkaran (Unsur-Unsur, Keliling, dan Luas)
Sudut Pusat Lingkaran
Sudut pusat adalah sudut terkecil yang dibentuk oleh dua jari-jari lingkaran. Titik sudut dari sudut pusat lingkaran merupakan titik pusat lingkaran.
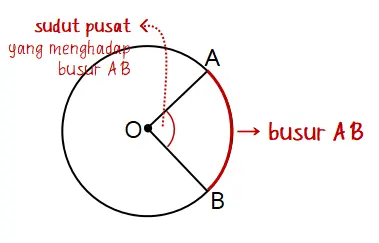
Misalkan, titik A dan B terletak pada busur lingkaran dengan titik pusat O. Ruas garis OA dan OB merupakan jari-jari lingkaran tersebut. Sudut terkecil yang dibetuk oleh titik A, O, dan B adalah ∠AOB. Sudut ini merupakan sudut pusat lingkaran yang menghadap busur AB.
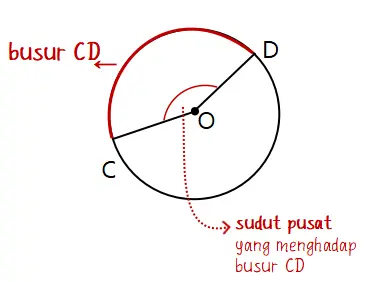
Contoh lain, titik C dan titik D terdapat pada busur lingkaran dengan pusat O. Sehingga OC dan OD merupakan jari-jari lingkaran tersebut. Sudut terkecil yang terbentuk adalah ∠COD yang menghadap busur CD. Sudut ini merupakan sudut pusat lingkaran.
Gambar sudut pusat lingkaran:
Baca Juga: Panjang Busur dan Luas Juring Lingkaran
Sudut Keliling Lingkaran
Sudut keliling adalah sudut yang dibentuk oleh dua tali busur lingkaran. Tali busur lingkaran adalah garis lurus yang menghubungkan dua titik pada busur lingkaran.
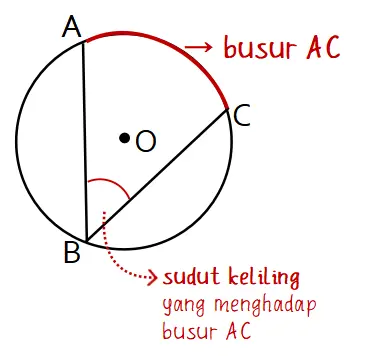
Sebagai contoh, titik A dan titik B terletak pada busur lingkaran. Sebuah ruas garis menghubungkan kedua titik tersebut sehingga menghasilkan garis AB. Garis AB merupakan tali busur lingkaran. Saat titik C juga terdapat pada lingkaran, tali busur BC dan AB membentuk sudut ABC. Sudut ABC merupakan sudut keliling yang menghadap busur AC.
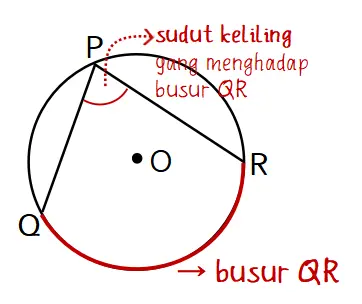
Contoh lain, titik P dan titik Q membentuk tali busur PQ. Sementara titik P dan R membentuk tali busur PR. Sudut QPR merupakan sudut keliling lingkaran yang menghadap busur PR.
Gambar sudut keliling:
Baca Juga: Garis Singgung Lingkaran Persekutuan Dalam dan Luar Lingkaran
Besar Sudut Pusat dan Sudut Keliling Lingkaran
Sudut pusat lingkaran sama dengan dua kali sudut keliling lingkaran yang menghadap busur yang sama. Sehingga perlu diperhatikan apa busur lingkaran yang berhadapan dengan sudutnya.
Misalkan, sudut AOB adalah sudut pusat lingkaran yang menghadap busur AB. Dan sudut ACB adalah sudut keliling lingkaran yang menghadap busur AB. Diketahui besar sudut ACB = 30o, maka besar sudut AOB = 2 × 30o = 60o.
Untuk setiap sudut keliling yang menghadap busur yang sama, besar sudutnya adalah sama besar. Misalkan ∠ADB dan ∠ACB adalah dua sudut keliling lingkaran yang menghadap busur AB. Besar sudut ACB adalah 30o, maka besar sudut ADB = sudut ACB = 30o.
Rumus sudut pusat dan sudut keliling:

Besar sudut pusat adalah dua kali besar sudut keliling yang menghadap busur yang sama.
Sehingga,
m∠AOB = 2× m∠APB
m∠AOB = 2× m∠AQB
Besar sudut keliling adalah setengah dari besar sudut pusat yang menghadap busur yang sama.
Sehingga,
m∠APB = 1/2× m∠AOB
m∠AQB = 1/2× m∠AOB
Besar sudut keliling yang menghadap busur yang sama adalah sama. Sehingga m∠APB = m∠AQB.
Baca Juga: Rumus Luas Tembereng dan Contoh Cara Menghitungnya
Contoh Soal dan Pembahasan
Soal sudut pusat dan sudut keliling lingkaran ada di bawah.
Contoh 1 – Jika besar ∠AOB adalah 40o maka besar ∠ACD adalah ….
Perhatikan gambar berikut!
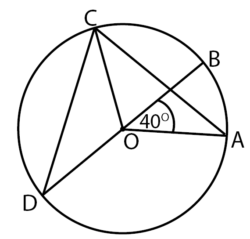
Jika besar ∠AOB adalah 40o maka besar ∠ACD adalah ….
A. 70o
B. 72o
C. 80o
D. 83o
Pembahasan:
Garis DB merupakan garis lurus. Pada garis BD terdapat ∠AOD dan ∠AOB yang saling berpelurus. INGAT!!! bahwa besar sudut pada garis lurus adalah 180o.
Sehingga, jumlah besar ∠AOD dan ∠AOB = 180o
∠AOD + ∠AOB = 180o
∠ AOD + 40o = 180o
Jadi, besar ∠AOD = 180o ‒ 40o = 140o
Sudut ACD dan ∠AOD adalah sudut pusat dan sudut keliling yang menghadap busur AD (menghadap busur yang sama). Sehingga besar sudut ACD (sudut keliling) sama dengan setengah dari besar sudut AOD (sudut pusat).
Besar ∠ACD = 70o
Besar ∠ACD = 1/2 × ∠AOD = 1/2 × 140o = 70o
Jadi, besar ∠ACD adalah 70o.
Jawaban: A
Contoh 2 – Besar ∠AOE adalah ….
Perhatikan gambar di bawah!
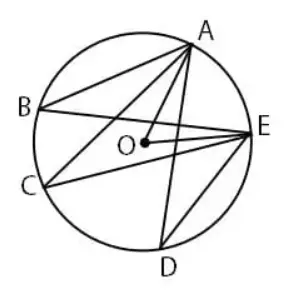
Titik O merupakan titik pusat lingkaran dan diketahui besar ∠ABE + ∠ACE + ∠ADE = 102o. Besar ∠AOE adalah ….
A. 34o
B. 51o
C. 64o
d. 68o
Pembahasan:
Sudut ABE, ACE, dan ADE adalah tiga sudut keliling yang menghadap busur yang sama yaitu busur AE. Sehingga ketiga sudut tersebut memiliki besar sudut yang sama.
Misalkan:
x = besar sudut ABE, ACE, dan ADE
Maka,
m∠ABE + m∠ACE + m∠ADE = 102o
x + x + x = 102o
3x = 102o
x = 102o : 3 = 34o
Sudut AOE adalah sudut pusat yang menghadap busur AE. Sudut ∠ABE, ∠ACE, dan ∠ADE adalah sudut keliling yang menghadap busur AE. Sehingga, besar ∠AOE sama dengan dua kali salah sudut keliling tersebut.
Besar ∠ABE = 34o
Besar ∠AOE = 2 × ∠ABE = 2 × 34o = 68o
Jadi, besar ∠AOE adalah 68o.
Jawaban: D
Baca Juga: Rumus Besar Sudut pada Segi Empat Tali Busur
Contoh 3 – Jika besar ∠OBC adalah 65o maka besar ∠AOC adalah ….
Perhatikan gambar lingkaran di bawah!
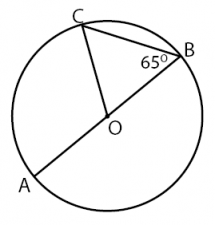
Jika besar ∠OBC adalah 65o maka besar ∠AOC adalah ….
A. 50o
B. 65o
C. 70o
D. 130o
Pembahasan:
Panjang OB = OC = jari-jari lingkaran. Sehingga segitiga BOC adalah segitiga sama kaki. Pada segitiga sama kaki, besar ketiga sudut yang menghadap kaki segitiga sama basar. Maka besar ∠OBC = ∠OCB = 65o.
Jumlah sudut dalam segitiga adalah 180o
∠OBC + ∠OCB + ∠BOC = 180o
65o + 65o + ∠BOC = 180o
130o + ∠BOC = 180o
∠BOC = 180o ‒ 130o = 50o
Garis AC merupakan garis lurus sehingga jumlah ∠BOC dan ∠AOC sama dengan 180o.
∠BOC + ∠AOC = 180o
50o + ∠AOC = 180o
∠AOC = 180o ‒ 50o = 130o
TRIK!!! CARA CEPATnya:

Jadi, Jika besar ∠OBC adalah 65o maka besar ∠AOC adalah 130o.
Jawaban: D
Sekian pembahasan mengenai sudut pusat dan sudut keliling lingkaran. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Mantap pak buk
Halo Rahesa, terimakasih kunjungan dan komentarnya.
Tau dari mana ob ama oc panjangnya sama?
Karna ob sama oc kan jari” lingkaran
Halo Fajar Kim, OB dan OC pada lingkaran tersebut meruakan jari-jari lingkaran, di mana panjang jari-jari lingkaran akan selalu sama pada lingkaran tersebut.
Halo Vii, terimakasih bantuan balasannya, salam sukses selalu!