Materi peluang SMP Kelas 9 membahas besar nilai yang menunjukkan kemungkinan terjadinya suatu kejadian. Misalnya, peluang hari akan hujan dinyatakan sebagai P(hujan) = 0,6. Artinya, besar potensi hujan hari ini adalah 0,6 atau 60%. Sisanya yaitu 0,4 = 40% adalah besar kemungkinan hari ini tidak hujan, PC(hujan) = 0,4.
Besar peluang suatu kejadian ditentukan oleh banyak kejadian dan banyak ruang sampel. Apa itu ruang sampel dan apa itu titik sampel pada bahasan materi peluang SMP? Bagaimana cara menentukan besar peluang suatu kejadian? Sobat idschool dapat mencari tahu jawabannya melalui ulasan materi peluang smp berikut,
Daftar isi:
Titik Sampel dan Ruang Sampel
Peluang adalah nilai/angka yang menunjukan kemungkinan terjadinya suatu kejadian. Besar peluang bergantung dari banyak ruang sampel dan titik sampel suatu kejadian. Sehingga perlu untuk mengetahui apa itu ruang sampel dan apa itu titik sampel terlebih dahulu sebelum menentukan besar peluang suatu kejadian.
Ruang sampel adalah himpunan dari semua hasil percobaan yang mungkin terjadi. Sedangkan titik sampel adalah anggota yang ada di dalam ruang sampel. Antara suatu kejadian dengan kejadian lain memiliki ruang sampel yang berbeda.
Cara mengetahui ruang sampel dan titik sampel dari suatu kejadian dapat dilakukan dengan mendaftar semua kemungkinan yang dapat terjadi.
A) Pelemparan n Buah Koin
Pada pelemparan sebuah koin memiliki dua kejadian yang daoat terjadi. Dua kejadian tersebut terdiri dari munculnya sisi berupa angka (A) dan munculnya sisi berupa gambar (G). Sehingga banyak ruang sampel untuk kejadian pelemparan sebuah koin adalah n(S) = 2.
Di sini, titik sampel pada pelemparan sebuah koin adalah munculnya permukaan angka atau munculnya permukaan gambar. Sedangkan ruang sampelnya adalah semua titik sampel yaitu munculnya pemukaan angka dan munculnya permukaan gambar.
Untuk pelemparan 2 buah koin, kejadian yang dapat terjadi adalah munculnya dua sisi berupa angka, satu sisi angka dan satu sisi gambar, satu sisi gambar dan satu sisi angka, serta keduanya sisi berupa angka.
Titik sampel pada pelemparan dua koin dapat dituliskan {(A, A); (A, G); (G, A); {G, G}}. Banyak ruang sampel pada pelemparan dua koin adalah n(S) = 4.
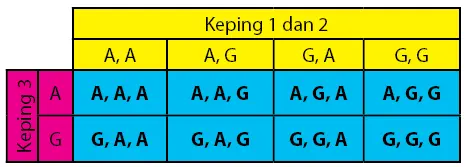
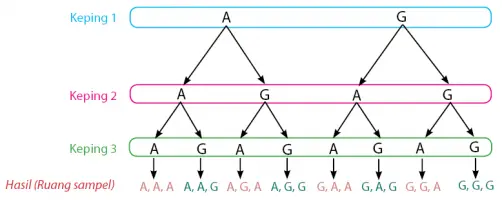
Lain lagi untuk ruang sampel dan titik sampel pada pelemparan tiga koin yang dilambungkan bersama-sama.
Cara menentukan banyak ruang sampel dan titik sempel dari kejadian pelemparan 3 buah koin dapat menggunakan tabel atau diagram pohon seperti yang yang dilakukan pada cara berikut.
Diperoleh bahwa banyak ruang sampel sama dengan 8 titik sampel, n(S) = 8. Daftar titik sampel untuk kejadian pelemparan tiga koin meliputi {(A, A, A); (A, A, G); (A, G, A); (A, G, G); (G, A, A); (G, A, G); (G, G, A); (G, G, G)}.
Secara umum, banyak ruang sampel dari kejadian pelemparan n koin sama dengan n(S) = 2n. Untuk banyak koin n = 3, banyaknya ruang sampel adalah n(S) = 23 = 8.
B) Pelemparan Dadu
Selain kejadian pelemparan n buah koin, materi peluang SMP juga sering membahas kejadian pada pelemparan dadu.
Pada pelemparan sebuah dadu memuat titik sampel munculnya mata dadu 1, 2, 3, 4, 5, dan 6. Ruang sampel pada pelemparan sebuah dadu ada sebanyak n(S) = 6 yang merupakan jumlah semua titik sampel kejadian.
Untuk kejadian pelemparan dua dadu memiliki banyak ruang sampel n(S) = 36. Titik-titik sampel kejadian pelemparan dua dadu terdapat pada tabel berikut.
| mata dadu | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | (1, 1) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) |
| 2 | (2, 1) | (2, 2) | (2, 3) | (2, 4) | (2, 5) | (2, 6) |
| 3 | (3, 1) | (3, 2) | (3, 3) | (3, 4) | (3, 5) | (3, 6) |
| 4 | (4, 1) | (4, 2) | (4, 3) | (4, 4) | (4, 5) | (4, 6) |
| 5 | (5, 1) | (5, 2) | (5, 3) | (5, 4) | (5, 5) | (5, 6) |
| 6 | (6, 1) | (6, 2) | (6, 3) | (6, 4) | (6, 5) | (6, 6) |
Cara membaca tabel: untuk (5, 6) berarti muncul mata dadu 5 pada dadu pertama dan muncul mata dadu 6 pada dadu kedua.

Baca Juga: Materi Pangkat dan Bentuk Akar
Peluang Suatu Kejadian dan Frekuensi Harapan
Peluang suatu kejadian merupakan nilai/angka yang menyatakan besar persentase keberhasilan dari terjadinya suatu kejadian. Sementara frekuensi harapan merupakan banyak kejadian berhasil dari suatu kejadian/percobaan.
Rumus materi peluang SMP dari suatu kejadian dan banyak frekuensi harapan terdapat persamaan berikut.
Rumus Peluang Kejadian
Peluang suatu kejadian adalah perbandingan antara banyaknya kejadian yang berhasil dengan banyaknya seluruh kejadian. Untuk banyak kejadian A adalah n(A) dan banyak seluruh kejadian n(S), besar peluang kejadian A sama dengan nilai yang dihasilkan rumus P(A) berikut.
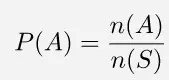
Keterangan:
P(A) = besar peluang kejadian A
n(A) = banyaknya kejadian A
n(S) = banyak kejadian (jumlah ruang sampel)
Jika diketahui Ac adalah bukan merupakan kejadian A maka besar peluang tidak terjadi kejadian A adalah P(Ac) = 1 ‒ P(A).
Peluang suatu kejadian bernilai antara 0 dan 1 atau dapat dinotasikan 0≤P(A)≤1. Apabila nilai P(A) = 0 diartikan bahwa kejadian A mustahil untuk terjadi sedangkan jika nilai P(A) = 1 diartikan bahwa kejadian A pasti akan terjadi.
Bagaimana penggunaan rumus peluang kejadian terdapat pada langkah penyelesaian soal di bawah.
Soal materi peluang SMP #1:
Sebuah dadu dilempar sekali. Peluang muncul mata dadu faktor dari 6 adalah ….
Jawab:
Titik sampelnya adalah kejadian muncul mata dadu faktor dari 6 yaitu muncul mata dadu 1, 2, 3, dan 6. Sehingga banyak kejadian muncul mata dadu faktor dari 6 adalah n(A) = 4.
Pada pelemparan sebuah dadu, banyak ruang sampel kejadian adalah n(S) = 6 yaitu munculnya mata dadu 1, 2, 3, 4, 5, dan 6. Sehingga besar peluang muncul mata dadu faktor dari 6 adalah.
Jadi, peluang muncul mata dadu faktor dari 6 adalah (C) 2/3.
Baca Juga: Cara Menyelesaikan Soal 2 Perbandingan
Frekuensi Harapan
Frekuensi banyaknya harapan kejadian A dari n kali percobaan sama dengan besar peluang kejadian A dikali banyak percobaan.
Frekuensi harapan dapat dihitungmenggunakan persamaan di bawah.
Fh(A) = P(A) × n
Keterangan:
Fh(A) = frekuensi harapan kejadian A
P(A) = nilai peluang munculnya kejadian A
n = banyak percobaan
Bagaimana penggunaan rumus frekuensi harapan terdapat pada langkah penyelesaian soal di bawah.
Soal materi peluang SMP #2:
Tiga mata uang dilempar sekaligus sebanyak 80 kali. Frekuensi harapan muncul dua sisi angka adalah ….
A. 20 kali
B. 25 kali
C. 30 kali
D. 40 kali
Jawab:
Dari soal diketahui banyak percobaan dilakukan sebanyak n = 80 kali menggunakan tiga mata uang.
Titik-titik sampel pada percobaan menggunakan tiga mata uang adalah {(A, A, A); (A, A, G); (A, G, A); (A, G, G); (G, A, A); (G, A, G); (G, G, A); (G, G, G)}.
Sehingga,
- Banyak kejadian muncul dua sisi angka: n(AA) = 3
- Banyak kejadian: n(S) = 8
Besar peluang muncul dua sisi angka:
Menghitung frekuensi harapan muncul dua sisi angka:
Fh(2A) = 3/8 × 80
= 3 × 10
= 30 kali
Jadi, frekuensi harapan muncul dua sisi angka adalah (C) 30 kali.
Baca Juga: Perbandingan Senilai dan Berbalik Nilai
Contoh Soal Materi Peluang SMP dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan materi peluang SMP di atas.
Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pemabahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Materi Peluang SMP
Tiga koin dilambungkan sekali. Peluang muncul sedikitnya satu gambar adalah ….
Pembahasan:
Titik-titik sampel pada percobaan pelemparan 3 koin terdiri dari {(A, A, A); (A, A, G); (A, G, A); (A, G, G); (G, A, A); (G, A, G); (G, G, A); (G, G, G)}. Sehingga dapat diketahui banyak ruang sampel pada pelemparan tiga koin adalah n(S) = 8.
Titik sampel untuk kejadian muncul sedikitnya satu gambar adalah {(A, A, A); (A, A, G); (A, G, A); (A, G, G); (G, A, A); (G, A, G); dan (G, G, A)}. Banyak kejadian muncul sedikitnya satu gambar adalah n(>1G) = 7.
Menghitung peluang muncul sedikitnya satu gambar:
Jadi, peluang muncul sedikitnya satu gambar pada adalah n(>1G) = 7/8
Jawaban: A
Contoh 2 – Soal Materi Peluang SMP
Dua dadu dilemparkan bersamaan satu kali, peluang munculnya mata dadu berjumlah 10 adalah ….
A. 1/81
B. 1/12
C. 1/10
D. 1/15
Pembahasan:
Titik sampel dari pelemparan dua dadu adalah sebagai berikut.
| + | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Diperoleh banyaknya ruang sampel: n(S) = 36
Misalkan A adalah kejadian munculnya jumlah kedua dadu sama dengan 10. Kejadian A adalah . Sehingga banyak kejadian A adalah n(A) = 3.
Menhitung besar peluang munculnya jumlah kedua dadu = 10:
Jadi, peluang muncul kedua mata dadu berjumlah 10 adalah P(A) = 1/12
Jawaban: B
Contoh 2 – Soal Materi Peluang SMP
Roni diperbolehkan ibunya untuk mengambil satu permen dari sebuah kantong. Warna permen dalam kantong meliputi 6 merah, 5 kuning, 3 hijau, 3 biru, 4 coklat, 2 ungu, dan 7 oranye.
Berapa peluang Roni mengambil sebuah permen warna merah?
A. 10%
B. 20%
C. 25%
D. 50%
Pembahasan:
Berdasarkan keterangan pada soal dapat diperoleh beberapa informasi berikut.
- Banyak ruang sampel:
n(S) = 6 + 5 + 3 + 3 + 2 + 4 + 2 + 5
n(S) = 30 - Banyak permen merah: n(A) = 6
Peluang Roni mengambil sebuah permen warna merah:
Jadi, persentase peluang Roni mengambil sebuah permen warna merah adalah P(merah) 1/5×100% = 20%.
Jawaban: B
Demikianlah tadi ulasan materi peluang SMP beserta contoh soal dan cara mengerjakannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Sebenernya kurang paham loh, kalo nggak dijelasin secara langsung.
Kurang paham dengan pembelajarannya
Snagat bagus penjelasannya
Mudah dipelajari:”)
Bagusss:”)