Ada dua rumus persamaan garis lurus yaitu y – y1 = m(x – x1) dan y – y1/y2 – y1 = x – x1/x2 – x1. Dua rumus tersebut digunakan untuk dua bentuk soal yang berbeda. Penjelasan cara menggunakan rumus persamaan garis lurus ada di bawah.
Daftar isi:
- Rumus Persamaan Garis Lurus
- Rumus Persamaan Garis Lurus yang Saling Sejajar dan Tegak Lurus
- Contoh Penggunaan Rumus Persamaan Garis Lurus
Rumus Persamaan Garis Lurus
Ada dua rumus persamaan garis lurus yang diketahui. Dua rumus ini digunakan untuk dua kondisi yang berbeda. Kedua rumus ada di bawah.

1) Memiliki gradien m dan melalui 1 titik
Rumus garis lurus yang memiliki gradien m dan diketahui melalui 1 titik adalah y – y1 = m(x – x1). Keterangannya m adalah gradien garis lurus dan (x1, y1) adalah satu titik yang dilalui garis lurus.
Cara menggunakan rumusnya terdapat pada penyelesaian contoh soal di bawah.
Soal:
Tentukan persamaan garis yang memiliki gradien 3 dan melalui titik (–1, 2)!
Jawab:
Diketahui garis memiliki gradien 3 dan melalui satu titik (–1, 2). Maka m = 3, x1 = –1, dan y1 = 2.
Sehingga,
y – 2 = 3(x – (–1))
y – 2 = 3(x + 1)
3x – y + 3 + 2 = 0
3x – y + 5 = 0
Jadi, persamaan garis yang memiliki gradien 3 dan melalui titik (–1, 2) adalah 3x – y + 5 = 0.
2) Diketahui melalui 2 titik
Rumus persamaan garis lurus yang diketahui melalui dua titik:
Keterangannya (x1, y1) dan (x2, y2) adalah koordinat titik-titik yang dilalui oleh garis lurus. Cara menggunakan rumusnya ada pada penyelesaian contoh soal di bawah.
Soal:
Tentukan persamaan garis melalui titik (2, −5) dan (−3, 6)!
Jawab:
Diketahui dua titik yang dilalui garis yaitu (2, −5) dan (−3, 6). Maka x1 = 2, y1 = −5, x2 = −3, dan y2 = 6.
Sehingga cara menentukan persamaan garisnya dilakukan seperti berikut.
11(x − 2) = −5(y + 5)
11x + 5y = −3
Jadi, persamaan garis melalui titik (2, −5) dan (−3, 6) adalah 11x + 5y = −3.
Rumus Persamaan Garis Lurus yang Saling Sejajar dan Tegak Lurus
Dua buah garis lurus dapat memiliki hubungan saling sejajar. Yaitu saat dua garis lurus tidak memiliki titik potong. Selain itu, dua garis lurus dapat juga memiliki hubungan saling tegak lurus. Yaitu saat dua garis lurus berpotongan dan membentuk sudut siku-siku.
Garis lurus saling sejajar memiliki gradien yang sama. Sedangkan garis lurus saling tegak lurus memiliki gradien lawan kebalikannya.
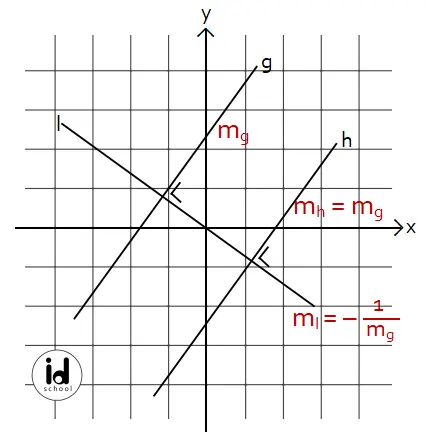
Misalkan diketahui tiga garis yaitu garis g, h, dan l. Garis g dan h sejajar, sementara garis g dan l saling tegak lurus. Diketahui gradien garis g adalah mg = 2. Maka gradien garis h adalah mh = mg = 2 dan gradien garis l adalah ml = –1/mg = –1/2.
Baca Juga: Cara Cepat Menentukan Persamaan Garis yang Saling Sejajar
Contoh Penggunaan Rumus Persamaan Garis Lurus
Cara menggunakan rumus garis lurus ada untuk menyelesaikan soal-soal di bawah.
Contoh 1
Persamaan garis yang melalui titik (-3, 5) dan tegak lurus garis 3x – 2y = 4 adalah ….
A. 2x + 3y – 9 = 0
B. 2x – 3y – 9 = 0
C. 3x + 2y + 19 = 0
D. 3x – 2y – 1 = 0
Pembahasan:
Persamaan garis 3x – 2y = 4 memiliki nilai gradien m = 3/2. Cari tahu rumus gradien terlebih dahulu jika belum tahu bagaimana cara menentukan gradien.
Garis lurus yang akan dicari persamaannya tegak lurus dengan garis 3x – 2y = 4. Sehingga gradien garis lurus yang akan dicari persamaannya adalah m = – 2/3.
Persamaan garis yang memiliki gradien m = 3/2 dan diketahui melalui titik (-3, 5) dicari menggunakan rumus y – y1 = m(x – x1).
Sehingga,
y – 5 = –2/3(x – (–3))
3(y – 5) = –2(x + 3)
3y – 15 = –2x – 6
2x + 3y – 9 = 0.
Jadi, persamaan garis yang melalui titik (-3, 5) dan tegak lurus garis 3x-2y=4 adalah 2x + 3y – 9 = 0.
Jawaban: A
Contoh 2
Perhatikan gambar berikut!
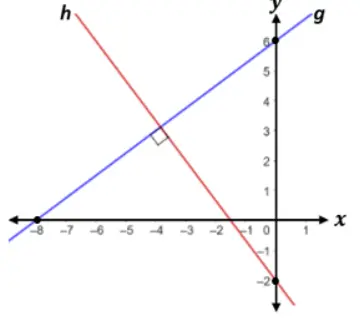
(1) Kemiringan garis g = –3/4
(2) Kemiringan garis h = –4/3
(3) Persamaan garis g adalah 3x – 4y = –24
(4) Persamaan garis h adalah 4x – 3y = 6
Pernyataan yang benar adalah ….
A. (1) dan (3)
B. (1) dan (4)
C. (2) dan (3)
D. (2) dan (4)
Pembahasan:
Dari gambar yang diberikan dapat digunakan untuk mencari nilai gradien garis g.
Garis g (garis warna biru) condong ke kanan. Sehingga gradiennya bernilai positif. Diketahui bahwa garis melalui titik (–8, 0) dan (0, 6). Sehingga nilai gradiennya adalah,
Kesimpulan: pernyataan (1) salah
Garis h tegak lurus dengan garis g, sehingga gradiennya adalah,
Kesimpulan: pernyataan (2) benar
Menentukan persamaan garis g:
y – 6 = 3/4(x – 0)
4(y – 6) = 3x
3x – 4y = –24 → Pernyataan (3) benar
Menentukan persamaan garis h:
y – (–2) = –4/3(x – 0)
3(y + 2) = –4x
4x + 3y = –6 → Pernyataan (4) salah
Jadi, pernyataan yang benar adalah (2) dan (3).
Jawaban: (C)
Contoh 3
Persamaan garis yang sejajar dengan garis yang melalui titik (2, 5) dan (−1, −4) adalah ….
A. y = ‒3x + 14
B. y = ‒1/3x + 6
C. y = 1/3x + 4
D. y = 3x ‒ 4
Pembahasan:
Gradien garis yang melalui titik (2, 5) dan (−1, −4) diketahui dengan rumus gradien berikut.
Garis lurus yang melalui titik (2, 5) dan (−1, −4) memiliki nilai gradien 3. Persamaan garis yang sejajar dengan garis tersebut juga memiliki gradien 3.
Nilai-nilai gradien persamaan garis lurus:
| Persamaan garis lurus | Gradien |
| y = ‒3x + 14 | ‒3 |
| y = ‒1/3x + 6 | ‒1/3 |
| y = 1/3x + 4 | 1/3 |
| y = 3x ‒ 4 | 3 |
Persamaan garis yang memiliki nilai gradien 3 adalah y = 3x ‒ 4. Jadi, persamaan garis yang sejajar dengan garis yang melalui titik (2, 5) dan (−1, −4) adalah y = 3x ‒ 4.
Jawaban: D
Sekian ulasan mengenai persamaan garis lurus. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!