Persamaan Garis Lurus yang Saling Sejajar +Cara Cepatnya

Dua garis dikatakan sejajar jika tidak memiliki titik potong. Pasangan garis lurus yang saling jejar memiliki gradien yang sama. Persamaan garis lurus yang saling sejajar adalah y – y₁ = m(x – x₁). Syaratnya nilai m pasangan garis sama.

Dua buah garis sejajar tidak akan memiliki titik potong sampai kapanpun. Meseki garis diperpanjang sampai panjangnya tak hingga.

Lebih lanjut mengenai persamaan garis lurus yang saling sejajar ada di bawah.

Daftas isi:

• Rumus Garis Lurus yang Saling Sejajar
• Cara Cepat Menentukan Persamaan Garis Lurus yang Saling Sejajar
• Contoh Soal dan Pembahasannya
  • Contoh 1 – Menentukan pasangan garis lurus sejajar
  • Contoh 2 – Soal Garis Saling Sejajar

Rumus Garis Lurus yang Saling Sejajar

Dua garis sejajar memiliki nilai gradien yang sama. Sebagai contoh, sebuah garis memiliki gradien m = 2. Semua garis yang sejajar dengan garis tersebut memiliki gradien yang sama yaitu 2.

Selanjutnya persamaan garis lurus yang saling sejajar dapat menggunakan rumus berikut.

Langkah – langkah menemukan persamaan garis yang saling sejajar:

1. Menentukan gradien garis lurus yang sejajar dengan garis yang akan dicari persamaannya
2. Gradien garis pertama sama dengan gradien garis kedua, sehingga m_g1 = m_g2
3. Perhatikan sebuah titik yang dilalui garis, misalkan (x₁, y₁)
4. Substitusi nilai gradien m_g2 dan titik (x₁, y₁) ke persamaan y – y₁ = m(x – x₁)
5. Selesaikan operasi hitung

Baca Juga: Persamaan Garis yang Saling Tegak Lurus

Cara Cepat Menentukan Persamaan Garis Lurus yang Saling Sejajar

Ada cara cepat yang dapat digunakan. Bagaimana cara cepat menemukan persamaan garis lurus yang saling sejajar ada di bawah.

Kesimpulan:
1) Persamaan garis ax + by + c = 0 akan sejajar dengan garis ax + by = a × x₁+ b × y₁
2) Persamaan garis ax – by + c = 0 akan sejajar dengan garis ax – by = a × x₁– b × y₁

Keterangan: x₁ dan y₁ adalah titik yang dilalui garis tersebut.

Contoh Soal dan Pembahasannya

Soal mengenai persamaan garis lurus sejajar ada di bawah.

Contoh 1 – Menentukan pasangan garis lurus sejajar

Persamaan garis yang melalui titik (4, 2) dan sejajar dengan garis 2x – y + 5 = 0 adalah ….
A. x + 2y + 6 = 0
B. 2x + y – 6 = 0
C. 2x – y – 6 = 0
D. 2x – y + 6 = 0

Pembahasan:
Pertama, akan dikerjakan dengan cara step by step. Kemudian akan dibandingkan hasilnya dengan cara cepat.

Menentukan gradien dari garis 2x – y + 5 = 0:

m = −^{koef. x}/_{koef. y}

m = −²/₋₁ = 2

Karena yang akan dicari adalah garis yang sejajar dengan garis 2x – y + 5 = 0 maka nilai gradien garis yang akan dicari adalah sama yaitu m₂ = 2.

Persamaan garis yang akan dicari melalui titik (4, 2):

y – y₁ = m₂ (x – x₁)

y – 2 = 2(x – 4)

2x – y – 8 + 2 = 0

2x – y – 6 = 0

Jadi, persamaan garis yang melalui titik (4, 2) dan sejajar dengan garis 2x – y + 5 = 0 adalah 2x – y – 6 = 0.

Bandingkan hasilnya dengan cara cepat berikut.

Persamaan garis melalui titik (4, 2) maka x₁ = 4 dan y₁ = 2.

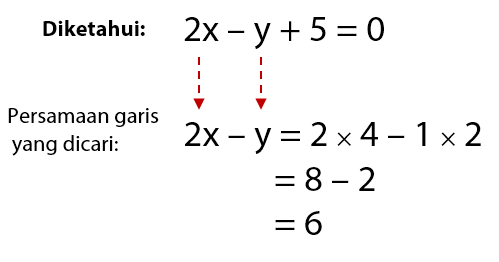
Diperoleh persamaan garis 2x – y = 6 → 2x – y – 6 = 0, hasil yang sama dengan cara pertama.

Jadi, persamaan garis yang melalui titik (4, 2) dan sejajar garis 2x – y + 5 = 0  adalah 2x – y – 6 = 0.

Jawaban: C

Baca Juga: Persamaan Garis Saling Tegak Lurus

Contoh 2 – Soal Garis Saling Sejajar

Persamaan garis yang melalui titik P(3, 2) dan sejajar dengan garis y = –4x + 6 adalah ….
A.    4x + y – 14 = 0
B. 4x + y + 14 = 0
C. 4x + y – 10 = 0
D. x + 4y + 10 = 0

Pembahasan:
Gradien garis y = – 4x + 6 adalah m₁ = – 4

Karena garis yang akan dicari sejajar maka m₂ = m₁ = – 4, sehinggan persamaan garis yang melalui titik P(3, 2) dan sejajar dengan garis y = – 4x + 6 dapat dicari seperti cara berikut.

y – y₁ = m₂(x – x₁)

y – 2 = – 4(x – 3)

4x + y – 2 – 12 = 0

4x + y – 14 = 0

Jadi, persamaan garis yang melalui titik P(3, 2) dan sejajar dengan garis y = – 4x + 6 adalah 4x + y – 14 = 0.

Jawaban: A

Demikianlah ulasan persamaan garis lurus yang saling sejajar beserta contoh soalnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.