Tali busur adalah ruas garis yang menghubungkan dua titik pada busur suatu lingkaran. Segi empat tali busur adalah bagun datar berbentuk segi empat yang setiap titik sudutnya berada pada busur lingkaran. Bentuk segi empat dapat berupa segi empat beraturan seperti persegi atau bentuk segi empat tidak beraturan. Setiap sudut yang dibentuk pada segi empat tali busur dalam lingkaran merupakan sudut keliling yang menghadap busur berbeda. Sehingga, besar keempat sudut yang terdapat pada bangun oleh empat tali busur adalah berbeda.
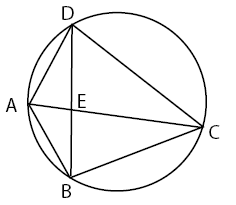
Sebuah lingkaran memiliki pusat di titik O dengan jari-jari r dan terdapat empat buah titik pada tepi lingkaran. Setiap dua titik yang terletak pada tepi lingkaran dapat dihubungan oleh sebuah ruas garis. Misalkan empat titik pada tepi lingkaran adalah titik A, B, C, dan D maka dapat diperoleh empat ruas garis. Keempat ruas garis tersebut adalah AB, BC, CD, dan DA yang keempatnya merupakan tali busur lingkaran. Keempat tali busur tersebut membentuk sebuah bangun segi empat ABCD. Untuk lebih jelasnya perhatIkan gambar di bawah.
Baca Juga: Unsur-Unsur, Keliling, dan Luas Lingkaran
Bagaimana hubungan antar sisi pada segi empat tali busur? Bagaimana hubungan dua diagonal pada segi empat tali busur? Berapa besar sudut yang terbentuk pada perpotongan antara dua tali busur? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Hubungan Diagonal Segi Empat Tali Busur
- Hubungan Sudut dalam Segi Empat Tali Busur
- Sudut Antara Dua Tali Busur
- Contoh Soal Empat Tali Busur dan Pembahasan
Hubungan Diagonal Segi Empat Tali Busur
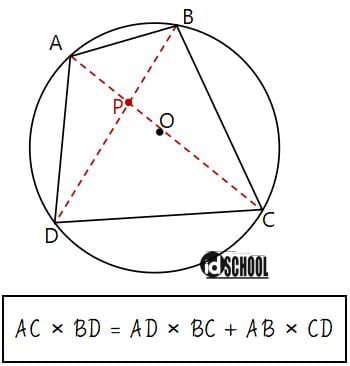
Pada bagun datar segi empat yang dibentuk oleh empat buah tali busur pada suatu lingkaran mempunyai empat sisi dan titik sudut. Jika titik sudut segi empat tali busur yang saling berhadapan dihubungkan maka akan diperoleh dua buah garis diagonal. Panjang kedua diagonal yang terbentuk memiliki hubungan dengan panjang empat sisi-sisi atau tali busurnya. Hubungan tersebut adalah hasil kali diagonal sama dengan jumlah perkalian sisi-sisi yang berhadapan.
Hasil Kali Diagonal = Jumlah Perkalian Sisi-Sisi yang Berhadapan
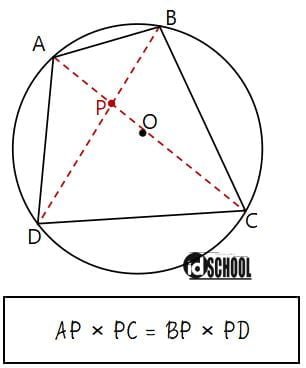
Kedua diagonal pada segi empat tali busur tersebut akan berpotongan pada satu titik, misalkan pada titik P. Bagian-bagian pada dua diagonal tersebut dapat dinyatakan dalam sebuah persamaan. Hubungan persamaan bagian-bagian diagonal adalah hasil kali antar jarak titik ke diagonal dan jarak diagonal ke titik yang dihubungkan oleh satu ruas garis adalah sama. Persamaan hubungan hasil kali bagian-bagian diagonal dinyatakan seperti persamaan berikut.
Hasil Kali Bagian-Bagian Diagonalnya adalah Sama
Baca Juga: Sudut Pusat dan Sudut Keliling pada Suatu Lingkaran
Hubungan Sudut dalam Segi Empat Tali Busur
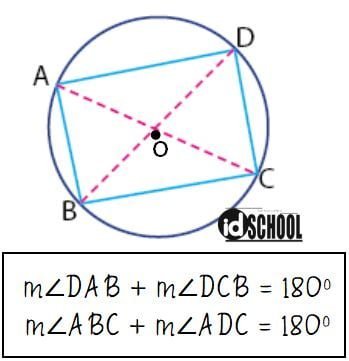
Segi empat tali busur adalah segi empat yang dibatasi oleh empat tali busur dengan keempat titik sudutnya terletak pada lingkaran. Pada segi empat tali busur, jumlah dua sudut saling berhadapan adalah 180o. Hubungan antar sudut yang terbentuk antar diagonal dua tali busur dinyatakan dalam persamaan yang di bahas di bawah.
Baca Juga: Lingkaran Dalam dan Luar Segitiga
Sudut Antara Dua Tali Busur
Tali busur lingkaran yang saling berpotongan akan membantuk suatu sudut. Perpotongan titik antar dua tali busur dapat terletak di dalam atau luar lingkaran. Banyaknya sudut yang terbentuk pada dua tali busur yang berpotongan di dalam lingkaran ada empat. Sedangkan sudut antara dua tali busur di luar lingkaran berjumlah satu yang merupakan perpanjangan ruas garis dari dua tali busur.
Tali busur yang berpotongan di dalam lingkaran
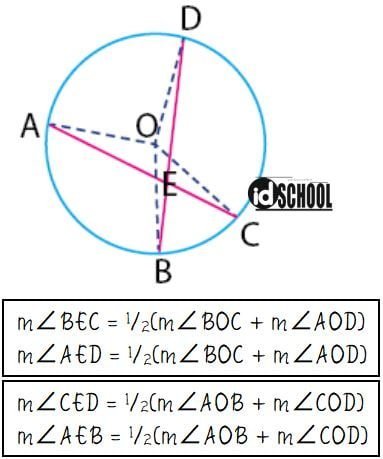
Besar sudut dari perpotongan tali busur mempunyai hubungan dengan sudut pusat yang saling menghadap busur sama. Misalkan ada dua tali busur AC dan BD yang berpotongan pasa satu titik yaitu titik E pada sebuah lingkaran dengan pusat O. Perpotongan dua tali busur tersebut membentuk dua pasang sudut yang besarnya sama untuk setiap pasang yaitu m∠AED = m∠BEC dan m∠CED dan m∠AEB.
Sudut pusat yang menghadap busur AD dan BC berturut-turut adalah ∠AOD dan ∠BOC. Sedangkan sudut pusat yang menghadap busur AB dan CD berturut-turut adalah ∠AOB dan ∠COD. Besar sudut yang terbentuk antara dua tali busur yang berpotongan di dalam lingkaran dapat diperoleh melalui persamaan di bawah.
Sudut Tali Busur yang Berpotongan di Luar Lingkaran
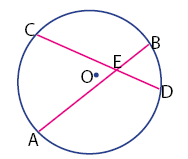
Sudut yang terbentuk antara dua tali busur yang berpotongan di luar lingkaran merupakan sudut dari perpanjangan ruas garis tali busur. Misalkan terdapat dua buah tali busur BC dan AD pada suatu lingkaran dengan pusat O. Perpanjangan dari kedua tali busur tersebut berpotongan pada titik E yang berada di luar lingkaran. Sudut yang terbentuk dari perpanjangan tali busur tersebut adalah ∠CED.
Selanjutnya, pada lingkaran terdapat dua busur yang dibentuk oleh titik AB dan CD. Sudut busat yang menghadap busur AB adalah ∠AOB dan sudut pusat yang menghadap busur CD adalah ∠COD. Besar ∠CED mempunya hubungan dengan kedua sudut pusat tersebut. Hubungan sudut tali busur yang berpotongan di luar lingkaran dan kedua sudut pusat dinyatakan seperti persamaan di bawah.
Baca Juga: Garis Singgung Lingkaran
Contoh Soal Empat Tali Busur dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman terkait bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Sudat Antara Dua Tali Busur yang Terpotong di Dalam Lingkaran
Pada gambar di bawah diketahui ∠BOD = 50o dan ∠AOC = 110o.
Besar ∠AEC adalah ….
A. 60o
B. 75o
C. 80o
D. 120o
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informai-informasi seperti berikut.
- Besar sudut pusat yang menghadap busur BD: m∠BOD = 50o
- Besar sudut pusat yang menghadap busur AC: m∠AOC = 110o
- AB dan CD adalah dua tali busur lingkaran yang berpotongan di dalam lingkarana pada titik E
Besar ∠AEC dapat dihitung menggunakan besar dua sudut pusat yang diketahui. Lihat kembali rumus pada sudut yang dibentuk antara dua tali busur yang berpotongan di dalam lingkaran, besar ∠BOD = 50o, dan besar ∠AOC = 50o.

Menghitung besar ∠AEB:
m∠AEC = 1/2 (m∠AOC + m∠DOB)
m∠AEB = 1/2 (110o + 50o) = 1/2 × 160o = 80o
Jawaban: D
Contoh 2 – Soal Hubungan Segi Empat Tali Busur
Perhatikan gambar di bawah!
Diketahui segi empat tali busur ABCD dengan AE = 3 cm, AC = 15 cm, dan BE = 9 cm. Panjang BD adalah ….
A. 15 cm
B. 14 cm
C. 13 cm
D. 12 cm
Pembahasan:
Berdasarkan keterangan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Panjang AE = 3 cm
- AC = 15 cm
AC = AE + CE
CE = AC ‒ AE
CE = 15 ‒ 3 = 12 cm - BE = 9 cm
Berdasarkan sifat segi empat tali busur dapat diperoleh persamaan yang akan digunakan untuk mendapatkan panjang DE.
BE × DE = AE × CE
9 × DE = 3 × 12
9 × DE = 36
DE = 36/9 = 4 cm
Jadi, panjang BD = BE + DE = 9 + 4 = 13 cm
Jawaban: C
Contoh 3 – Soal Hubungan Segi Empat Tali Busur

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Besar ∠BAC: m∠BAC = (2x + 10)o
- Besar ∠ABC: m∠ABC = 5xo
- m∠BCD = yo
- m∠CDA = 45o
Berdasarkan sifat sudut-sudut pada segi empat tali busur dapat diperoleh dua persamaan seperti di bawah.
- 5xo + 45o = 180o
- (2x + 10)o + yo = 180o
Menghitung nilai x:
5xo + 45o = 180o
5xo = 180o ‒ 45o
xo = 135o : 5 = 27o
Menentukan nilai y:
(2x + 10)o + yo = 180o
2×27o + 10o + yo = 180o
54o + 10o + yo = 180o
yo = 180o ‒ 54o ‒10o = 116o
Besar ∠BCD = y = 116o
Jawaban: D
Oke, demikian tadu ulasan materi segi empat tali busur dan sudut antara dua tali busur. Tereimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Unsur-unsur, Keliling, dan Luas Lingkaran