Jari-Jari Lingkaran Dalam dan Luar Segitiga +Contoh Soalnya

Pada lingkaran dalam dan luar segitiga selalu memiliki tiga titik potong. Lingkaran dalam segitiga adalah sebuah lingkaran terbesar dalam sebuah segitiga. Sedangkan lingkaran luas segitiga adalah lingkaran terkecil yang memuat sebuah segitga.

Terdapat hubungan antara jari-jari lingkaran dan luas segitiga pada lingkaran dalam dan luar segitiga. Bagaimana hubungannya? Bahasan lebih lanjut mengenai lingkaran dalam dan luas segitiga ada di bawah.

Daftar isi:

• Lingkaran Dalam Segitiga
• Lingkaran Luar Segitiga
• Luas Segitiga
• Contoh Soal Lingkaran Dalam dan Luar Segitiga
  • Contoh 1
  • Contoh 2

Baca Juga: Unsur-Unsur, Keliling, dan Luas Lingkaran

Lingkaran Dalam Segitiga

Sebuah lingkaran berada di dalam segitiga ABC yang panjang sisinya a, b, dan c. Setiap sisi segitiga menyinggung lingkaran. Sehingga ada tiga titik potong antara lingkaran dan segitiga.

Jari-jari lingkaran dalam segitiga sama dengan luas segitiga dibagi setengah keliling segitiga.

Baca Juga: Sudut Pusat dan Sudut Keliling pada Lingkaran

Lingkaran Luar Segitiga

Bentuk berikutnya adalah sebuah lingkaran berjari-jari r yang terdapat di luar segitiga ABC. Diketahui bahawa setiap sisi segitiga menyinggung lingkaran sehingga terdapat 3 titik singgung. Antara segitiga dan lingkaran tersebut memiliki hubungan antara luas segitiga dan panjang jari-jari lingkaran. luar segitiga.

Sisi-sisi segitiga ABC memiliki panjang sisi sama dengan a, b, dan c. Ketiga sisi segitiga yang diketahui dapat digunakan untuk mengetahui besar luas segitiga atau kelilingnya. Dari luas tersebut kemudian dapat digunakan untuk mendapatkan panjag jari-jari lingkaran dalam segitiga.

Jari-jari lingkaran tersebut dapat dihitung menggunakan rumus jari-jari lingkaran luar segitiga seperti persamaan di bawah.

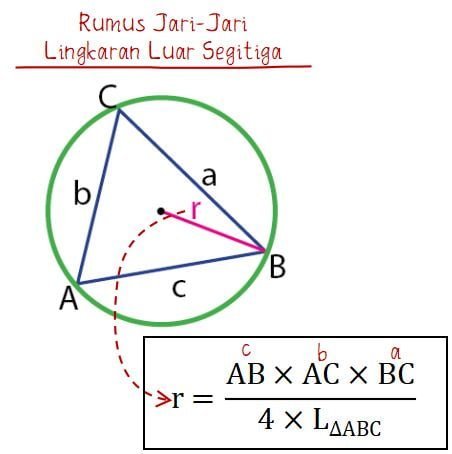
Baca Juga: Garis Singgung Lingkaran (Persekutuan Dalam dan Persekutuan Luar)

Luas Segitiga

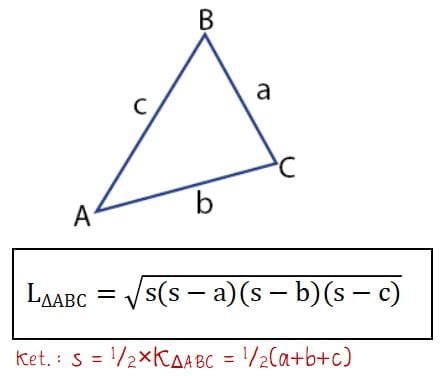
Sedangkan pada segitiga tidak beraturan atau segitiga sembarang, bagian sisi dan alas segitiga tidak dapat ditentukan. Untuk menghitung luas segitiga tak beraturan diperlukan rumus yang berbeda.

Kedua rumus segitiga yaitu segitiga beraturan dan tak beraturan diberikan seperti persamaan di bawah.

Baca Juga: Panjang Busur, Luas Juring, dan Luas Tembereng

Contoh Soal Lingkaran Dalam dan Luar Segitiga

Beberapa contoh soal lingkaran dalam dan luar segitiga ada di bawah.

Contoh 1

Perhatikan gambar di bawah!

Jika panjang AC dan BC berturut-turut 8 cm dan 15 cm maka panjang jari-jari lingkaran dalam segitiga tersebut adalah ….
A.  5 cm
B.  3,5 cm
C.  3 cm
D.  2,5 cm

Pembahasan:
Gambar pada soal merupakan lingkaran dalam segitiga. Untuk mengetahui besar jari-jari dari lingkaran tersebut digunakan rumus jari-jari lingkaran dalam segitiga.

Sebelumnya, kita perlu mencari sisi miring AB, keliling segitiga ABC, nilai s, dan luas segitiga ABC terlebih dahulu.

AB² = AC² + BC²
= 8² + 15²
= 64 + 225 = 289

Sehingga,
AB² = 289
AB = √289 = 17 cm

Keliling segitiga ABC:
K_ΔABC = AB + AC + BC
K_ΔABC = 17 + 8 + 15 = 40 cm

Mencari nilai nilai s:
s = ¹/₂ × K_ΔABC
s = ¹/₂ × 40 = 20 cm

Mencari luas segitiga ABC:
L_ΔABC = ¹/₂ × AC × BC
L_ΔABC = ¹/₂ × 8 × 15 = 60 cm²

Jadi, panjang jari-jari lingkaran dalam segitiga tersebut sama dengan r = ^LΔABC/_s= ⁶⁰/₂₀ = 3 cm.

Jawaban: C

Contoh 2

Perhatikan gambar berikut!

Luas lingkaran di atas adalah ….
A. 101⁵¹/₂₂₄ cm²
B. 100⁵¹/₂₂₄ cm²
C. 101⁵¹/₂₄₄ cm²
D. 100⁵¹/₂₄₄ cm²

Pembahasan:

Untuk mengetahui luas daerah yang diarsir, kita perlu mencari jari-jari lingkaran terlebih dahulu. Sebelumnya, kita juga perlu mencari Keliling segitiga ABC, nilai s, dan segitiga ABC terlebih dahulu.

Menghitung keliling ΔABC:
K_ΔABC = AB + BC + CA
K_ΔABC = 21 + 10 + 17 = 48 cm

Menghitung nilai s:
s = ¹/₂ × K_ΔABC
s = ¹/₂ × 48 = 24 cm

Karena segitiga di luar lingkaran merupakan segitiga tidak beraturan, maka luas diperoleh dengan cara berikut.

L_ΔABC = √[24×(24 – 10)×(24 – 17)×(24 – 21)]

= √[24 × 14 × 7 × 3]

= √7.056 = 84 cm²

 Menghitung nilai jari-jari lingkaran:

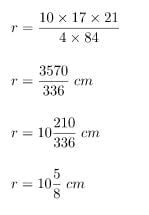
Menghitung luas lingkaran:

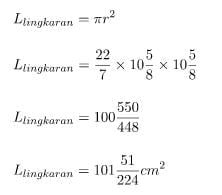
Jadi, luas lingkaran di atas adalah 101⁵¹/₂₂₄ cm²

Jawaban: A

Sekian pembahasan materi lingkaran dalam dan luar segitiga. Terimakasih sudah berkunjung ke idschool.net, semoga bermanfaat!