Contoh Soal Kesamaan Suku Banyak

Kesamaan berasal dari kata dasar sama, artinya materi kesamaan suku banyak berhubungan dengan sama. Bagaimana? Masih bingung?? Maksudnya di sini adalah menyelesaikan permasalahan suku banyak dengan pedoman kesamaan antar variabelnya. Contoh soal kesamaan suku banyak merupakan variasi soal atau pengembangan materi dasar dari suku banyak itu sendiri. Pembahasan soal kesamaan suku banyak berkaitan erat dengan variabel yang sama.

Gambarannya seperti ini, jika terdapat tiga pasang sandal yang diletakkan di tempat berbeda. Semua sandal sebelah kiri berada di sebelah kiri batas dan semua sendal sebelah kanan berada di sebelah kanan batas. Sandal tersebut akan terpakai secara tepat jika dipasangkan sesuai dengan pasangannya. Perhatikan gambar berikut.

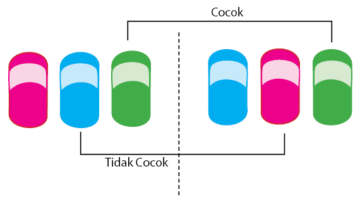
Sama dengan analogi pasangan sandal di atas. Permasalahan dalam kesamaan suku banyak diselesaikan dengan menyamakan koefisien dengan variabelnya. Penyelesaian contoh soal kesamaan suku banyak dapat lebih jelas ketika langsung melihat penyelesaian soalnya. Namun sebelumnya perhatikan prinsip kesamaan suku banyak antara dua bentuk suku banyak f(x) dan g(x) berikut.

Baca Juga: Operasi Suku Banyak: Penjumlahan, Pengurangan dan Perkalian

Kesamaan Suku Banyak

Misalkan diketahui dua buah suku banyak sebagai berikut:

• f(x) = a_nxⁿ + a_{n – 1}x^{n – 1} + … + a₂x² + a₁x + a₀
• g(x) = b_nxⁿ + b_{n – 1}x^{n – 1} + … + b₂x² + b₁x + b₀

Jika diketahui nilai f(x) sama dengan g(x) maka dapat diperoleh kesimpulan suatu kesamaan dari suku banyak tersebut. Kesamaan yang diperoleh merupakan kesamaan dengan variabel yang sama.

• a_n = b_n
• a_{n – 1} = b_{n – 1}
• …
• a₁ = b₁
• a₀ = b₀

Selanjutnya, perhatikan contoh soal kesamaan suku banyak yang akan diberikan berikut. Simak pembahasannya juga untuk menambah pemahaman sobat idschool.

Contoh Soal dan Pembahasan Kesamaan Suku Banyak

Perhatikan persamaan di bawah!

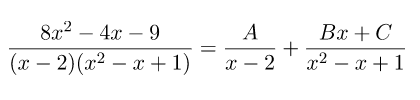
Nilai A + B + C = ….
A. 11
B. 12
C. 13
D. 14
E. 15

Pembahasan:
Langkah pertama adalah menyamakan penyebut dari kedua ruas seperti yang dilakukan pada cara di bawah.

Berdasarkan sifat kesamaan suku banyak diperoleh persamaan-persamaan berikut.

• Kesamaan 1: A + B = 8 → A = 8 – B 
• Kesamaan 2: A + 2B – C = 4
  Substitusi nilai A = 8 – B pada persamaan A + 2B – C = 4
  8 – B + 2B – C = 4
  B – C = 4 – 8
  B – C = –4
  C = B + 4 

• Kesamaan 3: A – 2C = –9
  Substitusi nilai A = 8 – B  dan C = B + 4 pada persamaan A – 2C = –9.
  – B + 8 – 2( B + 4) = – 9
  – 3B = – 9 → B = 3
  Diperoleh nilai B = 3

Selanjutnya, substitusi nilai B pada persamaan A = 8 – B dan C = B + 4 untuk mendapatkan nilai A dan C.

• A = 8 – B = 8 – 3 = 5
• C = B + 4 = 3 + 4 = 7

Jadi, nilai A + B + C = 5 + 3 + 7 = 15

Jawaban: E

Sekian materi mengenai contoh soal kesamaan suku banyak. Jika ada bagian yang salah karena kurang teliti dalam menghitung bisa tinggalkan komentar di bawah. Jika ada bagian yang kurang jelas juga bisa ditanyakan lewat kolom komentar. Terimakasih sudah mengunjungi idschool.net, semoga bermanfaat!

Baca Juga: Teorema Sisa dan Teorema Faktor Pada Suku Banyak