Garis singgung lingkaran adalah suatu garis lurus yang memiliki satu titik potong dengan lingkaran. Ada tiga bentuk rumus persamaan garis singgung yang akan diulas pada halaman ini. Tiga bentuk persamaan garis singgung yang ada digunakan untuk menyelesaikan tipe soal yang berbeda. Dengan kata lain, setiap bentuk rumus persamaan garis singgung lingkaran yang digunakan menyesuaikan tipe soal yang akan diselesaikan.
Rumus persamaan garis singgung bentuk pertama digunakan pada garis singgung yang melalui titik pada lingkaran. Bentuk kedua, persamaan garis singgung lingkaran yang digunakan untuk menentukan persamaan garis yang melalui satu titik di luar lingkaran. Untuk bentuk ketiga, rumus persamaan garis singgung yang diguanakan untuk menentukan persamaan garis lingkaran yang diketahui nilai gradiennya (m).
Bentuk umum garis singgung lingkaran yang dihasilkan dapat dinyatakan dalam persamaan garis lurus. Contoh bentuk umum persamaan garis lurus tersebut adalah ax + by + c = 0, ax + by = c, atau y = mx + c.
Bagaimana saja bentuk rumus persamaan garis singgung lingkaran? Bagaraimana cara menentukan perasamaan garis singgung linkaran? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Baca Juga: 3 Bentuk Persamaan Lingkaran (Rumus Pusat dan Jari-Jari Lingkaran)
Rumus Persamaan Garis Singgung Lingkaran yang Diketahui Melalui Sebuah Titik
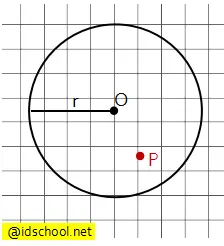
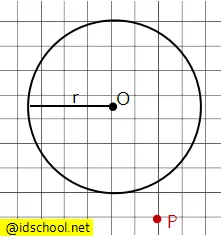
Sebuah garis lurus dapat melalui sebuah titik koordinta. Letak kedudukan titik terhadap lingkaran dapat berada di dalam, pada, atau di luar lingkaran. Tiga bentuk kedudukan titik terhadap lingkaran tersebut ada pada gambar berikut.
Letak kedudukan titik terhadap lingkaran memengaruhi rumus persamaan garis singgung lingkaran yang akan digunakan. Sehingga perlu dipastikan dahulu bagaimana kedudukan titik koordinat yang dilalui garis lurus terhadap lingkaran.
Kedudukan titik terhadap lingkaran dapat dicari tahu dengan cara subsitusi nilai absis dan ordinat titik yang dilalui garis lurus pada persamaan lingkaran. Jika diperoleh sebuah persamaan maka titik berada pada lingkaran. Jika diperoleh sebuah pertidaksamaan lebih besar maka titik berada di luar lingkaran.
1) Rumus Garis Singgung Lingkaran yang Melalui Sebuah Titik pada Lingkaran
Misalkan sebuah garis lurus menyinggung lingkaran dengan pusat P(a, b) dan jari-jari r pada titik Q(x1, y1). Titik potong garis tersebut adalah titik di mana titik Q terletak pada lingkaran.
Gambaran lingkaran, titik potong, dan garis singgung lingkaran diberikan seperti berikut.

Ada 3 (tiga) persamaan yang dapat digunakan untuk menentukan garis singgung lingkaran yang diketahui melalui satu titik. Jika titik singgung pada lingkaran adalah (x1, y1) maka persamaan garis singgung lingkaran menggunakan rumus pada tabel berikut.

Bagaimaan cara menentukan persamaan garis singgung lingkaran dengan soal diketahui sebuah titik pada lingkaran terdapat pada penyelesaian contoh di bawah.
Contoh Soal:
Tentukan persamaan garis singgung yang melalui satu titik Q(1, 4) pada lingkaran dengan persamaan (x + 2)2 + (y – 3)2 = 10!
Pembahasan:
Pertama, pastikan bahwa kedudukan titik Q(1, 4) terletak pada lingkaran. Caranya dengan subsitusi nilai titik koordinat pada persamaan lingkaran.
Mengetahui keudukan titik Q terhadap lingkaran:
(x + 2)2 + (y – 3)2
= (1 + 2)2 + (4 – 3)2
= 32 + 12
= 9 + 1 = 10
Diperoleh persamaan (x + 2)2 + (y – 3)2 = 10 yang artinya titik terletak pada lingkaran. Sehingga rumus persamaan garis singgung yang digunakan adalah:
(x – a)(x1 – a) + (y – b)(y1 – b) = r2
Menentukan persamaan garis singgung lingkaran:
(x+2)(1–2) + (y–3)(4–3) = 36
(x + 2)(–1) + (y – 3)(1) = 36
–x – 2 + y – 3 = 36
–x + y = 51
x – y + 51 = 0
Jadi, persamaan garis singgung yang melalui satu titik Q(1, 4) pada lingkaran yang memiliki persamaan (x + 2)2 + (y – 3)2 = 36 adalah x – y + 51 = 0.
Baca Juga: Persamaan Lingkaran yang Diketahui Melalui 3 Titik
2) Garis Singgung Lingkaran yang Melalui Satu Titik di Luar Lingkaran
Diketahui sebuah titik terletak di luar lingkaran. Dari titik tersebut dapat ditarik garis lurus yang menyinggung lingkaran. Sebuah titik potong antara garis lurus tersebut dengan titik pada lingkaran disebut titik singgung.
Misalkan titik Q(x1, y1) terletak di luar lingkaran, sedangkan titik R(x2, y2) dan S(x3, y3) terletak pada lingkaran. Garis lurus yang menghubungkan titik singgung lingkaran dengan titik Q(x1, y1) adalah garis singgung lingkaran. Sementara garis yang menghubungkan dua titik singgung yaitu RS disebut dengan garis polar.
Contoh ilustrasi persamaan garis singgung yang diketahui melalui di luar lingkaran terdapat pada gambar di bawah.

Langkah-langkah menentukan persamaan garis singgung lingkaran yang diketahui melalui satu titik di luar lingkaran terdapat pada tahapan penyelesaian berikut.
- Pertama:
Melakukan pemisalan garis singgung yaitu y – y1 = m(x – x1). Di mana m = kemiringan garis dan (x1, y1) = koordinat titik di luar lingkaran yang dilalui garis singgung.
- Kedua:
Substitusi persamaan y pada persamaan lingkaran sehingga diperoleh persamaan dalam variabel m.
- Ketiga:
Mencari persamaan nilai m dari persamaan diskriminan yang menghasilkan kedudukan garis terhadap lingkaran akan memotong pada satu titik (dipenuhi saat D = 0).
- Keempat:
Menyelesaikan persamaan dengan variabel m untuk mendapatkan nilainya.
- Kelima:
Substitusi nilai m yang didepat pada pemisalan persamaan y – y1 = m(x – x1) pada langkah pertama. Akan diperoleh persamaan garis lurus lingkaran yang dicari.
Contoh cara menentukan persamaan garis singgung lingkaran yang diketahui melalui satu titik di luar lingkaran dapat diamati seperti pada penyelesaian soal berikut.
Soal:
Tentukan persamaan garis singgung lingkaran yang melalui titik (3, 1) dengan persamaan x2 + y2 = 9!
Pembahasan:
Sebelumnya, pastikan bahwa titik (3, 1) berada di luar lingkaran. Caranya dengan substitusi nilai titik koordinat pada persamaan lingkaran.
Substitusi titik (3, 1) pada persamaan lingkaran x12 + y12:
= 32 + 12
= 9 + 1
= 10
Diperoleh nilai hasil substitusi x12 + y12 = 10 > 9 sehingga dapat disimpulkan bahwa letak titik (3, 1) berada di luar lingkaran.
Selanjutnya persamaan garis singgung lingkaran dicari dengan cara langkah penyelesaian berikut.
Pertama, misalkan persamaan garis singgung dengan persamaan: y – y1 = m(x – x1).
Diketahui titik (3, 1) dan persamaan garis y – y1 = m(x – x1). Substitusi titik (3, 1) ke persamaan garis sehingga diperoleh persamaan berikut.
Bentuk umum persamaan garis singgung lingkaran:
(y – 1) = m(x – 3)
y – 1 = mx – 3m
y = mx – 3m + 1
Kedua, substitusi persamaan y = mx – 3m + 1 ke persamaan lingkaran x2 + y2 = 9.
x2 + (mx–3m+1)2 = 9
x2 + mx(mx–3m+1) – 3m(mx–3m+1) +1(mx–3m+1) = 9
x2 + m2x2 – 3m2x + mx – 3m2x + 9m2 – 3m + mx – 3m + 1 = 9
(1 + m2)x2 – (6m2 – 2m)x + (9m2 – 6m – 8) = 0
Diperoleh persamaan kuadrat dengan nilai,
a = 1 + m2
b = –(6m2 – 2m) = 2m – 6m2
c = 9m2 – 6m – 8
Ketiga, menentukan nilai m dari persamaan nilai diskriminan D = b2 – 4ac. Di mana sebuah garis lingkaran akan menyinggung lingkaran saat nilai D = 0.
D = b2 – 4ac = 0
(2m – 6m2)2 – 4(m2+1)(9m2–6m– 8) = 0
4m2 – 24m3 + 36m4 – 36m4 + 24m3 + 32m2 – 36m2 + 24m + 32 = 0
24m + 32 = 0
Keempat, diperoleh persamaan 24m + 32 = 0. Nilai m dapat didapat dengan menyelesaikan persamaan tersebut.
Menentukan nilai m:
24m + 32 = 0
24m = –32
m = –32/24 = –4/3
Kelima, menentukan persamaan garis singgung yang akan dicari. Caranya dilakukan dengan subsitusi nilai m = –4/3 pada persamaan garis y = mx – 3m + 1.
Menentukan persamaan garis singgung lingkaran:
y = –4/3x – 3(–4/3) + 1
3y = –4x – 3(–4) + 3
3y = –4x + 12 + 3
4x + 3y – 15 = 0
Jadi, persamaan garis singgung lingkaran x2 + y2 = 9 yang melalui titik (3, 1) adalah 4x + 3y – 15 = 0.
Baca Juga: Cara Menentukan Persamaan Lingkaran yang Diektahui Melalui 3 Titik
Garis Singgung Lingkaran dengan Gradien Tertentu
Ada 3 (tiga) persamaan umum yang dapat digunakan untuk menentukan garis singgung lingkaran yang diketahui nilai gradiennya. Rumus yang akan digunakan tergantung pada persamaan lingkaran yang diketahui. Ada tiga rumus persamaan garis singgung lingkaran untuk tiga bentuk persamaan lingkaran yang berbeda.
Berikut ini adalah rumus umum persamaan garis singgung lingkaran untuk tiga bentuk persamaan lingkaran yang berbeda jika diketahui gradien garis singgung (m).

Contoh cara menentukan persamaan garis singgung lingkaran jika diketahui nilai gradien garis.
Contoh soal:
Sebuah lingkaran memiliki persamaan x2 + y2 = 9. Jika diketahui gradien garis singgung adalah 2, maka persamaan garis tersebut adalah ….
A. y = 2x + 3√5
B. y = 3x ‒ 2√5
C. y = 3x + 2√3
D. y = 3x ‒ 2√2
E. y = 3x + 2√5
Pembahasan:
Rumus persamaan garis singgung jika diketahui nilai gradien untuk persamaan lingkaran x2 + y2 = r2 ditunjukkan seperti pada rumus nomor 1.
Persamaan garis singgung lingkaran x2 + y2 = 9 dengan gradien m = 2:
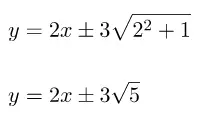
Jadi, persamaan garis singgung lingkaran x2 + y2 = 9 dengan gradien m = 2 adalah y = 2x + 3√5 atau y = 2x – 3√5.
Jawaban: A
Contoh soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap soal yang diberikan dilengkapi dengan pembahasannya. Sobat idshcool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Persamaan Garis Singgung Lingkaran
Salah satu persamaan garis singgung lingkaran x2 + y2 ‒ 10x + 4y + 4 = 0 yang sejajar dengan garis 8x ‒ 6y + 15 = 0 adalah ….
A. ‒3x + 4y ‒ 2 = 0
B. ‒3x + 4y ‒ 48 = 0
C. ‒3x + 4y + 2 = 0
D. ‒4x + 3y + 1 = 0
E. ‒4x + 3y + 5 = 0
Pembahasan:
Soal di atas menanyakan persamaan garis lurus yang memotong lingkaran x2 + y2 ‒ 10x + 4y + 4 = 0 pada satu titik. Di mana garis lurus yang akan dicari sejajar dengan garis 8x ‒ 6y + 15 = 0.
Garis 8x ‒ 6y + 15 = 0 memiliki nilai gradien m1 = ‒koef. x/koef. y = ‒8/‒6 = 4/3. Diketahui bahwa garis singgung lingkaran yang ditanyakan sejajar dengan garis 8x ‒ 6y + 15 = 0.
Sehingga nilai gradien garis singgung tersebut adalah m2 = m1 = 4/3.
Pusat lingkaran = P(‒1/2×(‒10), ‒1/2×4) = P(5, ‒2)
Jari-jari lingkaran:
r = √(52 + (‒2)2 ‒ 4)
r = √(25 + 4 ‒ 4)
r = √25 ± 5
Menentukan Persamaan garis singgung lingkaran:
y ‒ (‒2) = 4/3(x ‒ 5) ± 5√((4/3)2 + 1)
y + 2 = 4/3(x ‒ 5) ± 5√(16/9 + 16/9)
y + 2 = 4/3(x ‒ 5) ± 5×5/3
y + 2 = 4/3(x ‒ 5) ± 25/3
3(y + 2) = 4(x ‒ 5) ± 25
3y + 6 = 4x ‒ 20 ± 25
Dapat diperolah dua persamaan garis singgung lingkaran seperti berikut.
Persamaan (i):
3y + 6 = 4x ‒ 20 + 25
‒4x + 3y + 6 + 20 ‒ 25 = 0
‒4x + 3y + 1 = 0
Persamaan (ii):
3y + 6 = 4x ‒ 20 ‒ 25
‒4x + 3y + 6 + 20 + 25 = 0
‒4x + 3y + 51 = 0
Jadi, salah satu persamaan garis singgung lingkarannya adalah ‒4x + 3y + 1 = 0.
Jawaban: D
Contoh 2 – Soal Persamaan Garis Singgung Lingkaran
Salah satu garis singgung lingkaran x2 + y2 ‒ 25 = 0 yang diketahui melalui (7, 1) adalah ….
A. 7x + y ‒ 25 = 0
B. 4x + 3y ‒ 25 = 0
C. 3x + 4y ‒ 25 = 0
D. 3x ‒ 4y ‒ 25 = 0
E. x + 7y ‒ 25 = 0
Pembahasan:
Langkah pertama adalah menyelidiki kedudukan titik (7, 1) terhadap lingkaran x2 + y2 ‒ 25 = 0 untuk cara mana yang akan digunakan.
Menyelidiki letak kedudukan titik (7, 1) terhadap lingkaran x2 + y2 ‒ 25 = 0:
72 + 12 ‒ 25 = 49 + 1 ‒ 25 = 25 > 0.
Dapat diketahui bahwa letak titik berada di luar lingkaran. Sehingga cara menentukan persamaan garis singgung lingkaran dilakukan dengan langkah penyelesaian berikut.
Misalkan persamaana garis singgung lingkaran:
y ‒ 1 = m(x ‒ 7)
y ‒ 1 = mx ‒ 7m
y = mx ‒ 7m + 1
Subsitusui persamaan y = mx ‒ 7m + 1 pada persamaan lingkaran x2+y2‒25=0:
x2 + (mx ‒ 7m + 1)2 ‒ 25 = 0
x2 + mx(mx ‒ 7m + 1) ‒ 7m(mx ‒ 7m + 1) + 1(mx ‒ 7m + 1) ‒ 25 = 0
x2 + m2x2 ‒ 7m2x + mx ‒ 7m2x + 49m2 ‒ 7m + mx ‒ 7m + 1 ‒ 25 = 0
(1 + m2)x2 + (2m ‒ 14m2)x + 49m2 ‒ 14m ‒ 24 = 0
Diperoleh persamaan kuadrat dengan nilai a = 1 + m2; b = 2m ‒ 14m2; dan c = 49m2 ‒ 14m ‒ 24.
Membentuk persamaan nilai m:
D = b2 ‒ 4ac = 0
(2m ‒ 14m2)2 ‒ 4(1 + m2)(49m2 ‒ 14m ‒ 24) = 0
4m2 ‒ 56m3 + 196m4 ‒ 196m4 + 56m3 ‒ 100m2 + 56m + 96 = 0
‒96m2 + 56m + 96 = 0
12m2 ‒ 7m ‒ 12 = 0
Menentukan nilai m:
12m2 ‒ 7m ‒ 12 = 0
12m2 ‒ 16m + 9m ‒ 12 = 0
4m(3m ‒ 4) + 3(3m ‒ 4) = 0
(4m + 3)(3m ‒ 4) = 0
Dapat diperoleh dua nilai m:
- 4m + 3 = 0
4m = ‒3
m = ‒3/4
- 3m ‒ 4 = 0
3m = 4
m = 4/3
Persamaan garis singgung lingkaran untuk m = ‒3/4:
y = ‒3/4x ‒ 7(‒3/4) + 1
4y = ‒3x + 21 + 4
3x + 4y ‒ 25 = 0
Persamaan garis singgung lingkaran untuk m = 4/3:
y = 4/3x ‒ 7(4/3) + 1
3y = 4x ‒ 21 + 3
4x ‒ 3y ‒ 18 = 0
Jadi, salah satu garis singgung lingkaran x2 + y2 ‒ 25 = 0 di titik (7, 1) adalah 3x + 4y ‒ 25 = 0.
Jawaban: C
Demikianlah tadi ulasan bagaimana rumus persamaan garis singgung lingkaran beserta contoh penggunannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Persamaan-Persamaan pada Kurva dari Irisan Kerucut