Suku banyak atau polinomial adalah persamaan yang memiliki variabel dengan bilangan berpangkat. Cara menentukan nilai suku banyak (Polinomial) untuk suatu nilai x dapat dilakukan dengan cara substitusi nilai x ke persamaan suku banyak. Pangkat tertinggi dari sebuah polinomial disebut dengan derajat. Misalnya diberikan persamaan suku banyak x3 ‒ x + 3, suku banyak tersebut memiliki derajat 3. Secara umum, suku banyak atau polinomial dengan variabel x berderajat n dapat dituliskan dalam bentuk berikut.
Sebelumnya, sobat idschool pasti sudah mempelajari tentang persamaan kuadrat dan cara memfaktorkannya, yaitu persamaan yang memiliki pangkat tertinggi sama dengan 2. Bentuk persamaan kuadrat dapat termasuk dalam suku banyak atau sering disebut juga sebagai polinomial. Suku banyak atau polinomial dapat diartikan sebagai persamaan yang memiliki variabel dengan pangkat bertingkat. Contoh persamaan yang termasuk dalam suku banyak adalah x4 ‒ 1, 2x3 + x2 ‒ 5, dan lain sebagainya.
Tidak semua persamaan berpangkat tingkat disebut sebagai suku banyak. Persamaan yang memiliki pangkat negatif tidak termasuk dalam persamaan suku banyak. Kesimpulan yang dapat diambil adalah bilangan pangkat dari suku banyak harus merupakan bilangan cacah.
Contoh persamaan berpangkat yang bukan termasuk dalam suku banyak f(x) = 2x2 + 5x ‒ 3‒1 dan f(x) = 2x2 + 5x ‒ 3/x. Pesamaan f(x) seperti di atas memiliki variabel x dengan pangkat ‒1. Seperti kita ketahui bahwa ‒1 bukan merupakan bilangan cacah (bilangan bulat positif). Sehingga, persamaan f(x) bukan merupakan suku banyak.
Bagaimana cara menentukan nilai suku banyak untuk suatu nilai x? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Nilai Suku Banyak
Nilai dari suatu suku banyak atau polinomial di suatu titik dapat ditentukan melalui dua cara, yaitu cara substitusi dan horner. Cara substitusi diperoleh hanya dengan mengganti nilai variabel x dengan nilai di titik mana ingin diketahui nilai suku banyak f(x) tersebut. Sedangkan cara yang ke dua, cara horner, diperoleh dengan meletakkan koefisien-koefisien yang dimiliki variabel-varibelnya pada bagan dengan aturan yang telah ditentukan.
Simak pembahasan lengkapnya untuk kedua metode pada penjabaran materi di bawah.
Cara Substitusi
Persamaan suku banyak f(x) memiliki bentuk umum seperti yang telah dibahas sebelumnya. Nilai suku banyak di titik x = k dapat diperoleh dengan mengganti nilai x dengan k kemudian menghitungnya secara Aljabar biasa.
Nilai f(x) dengan bentuk umumnya di suatu titik x = k dinyatakan dalam persamaan di bawah.
f(x) = ankn + an ‒ 1kn ‒ 1 + . . . + a1k + a0
Untuk menambah pemahaman sobat idschool semuanya, perhatikan contoh soal di bawah.
Soal:
Nilai suku banyak f(x) = x3 + 3x2 + 3x + 1 pada titik x = 3 adalah ….
Jawab:
Mencari nilai suku banyak f(x) = x3 + 3x2 + 3x + 1 pada titik x = 3:
f(x) = x3 + 3x2 + 3x + 1
f(3) = (3)3 + 3(3)2 + 3(3) + 1
f(3) = 27 + 27 + 9 + 1 = 64
Jadi, nilai dari sukubanyak f(x) = x3 + 3x2 + 3x + 1 untuk x = 3 adalah 64.
Cara Skema/Bagan (Cara Horner)
Langkah pertama mencari nilai suku banyak f(x) untuk x = k dengan cara horner adalah meletakkan koefisien secara berurutan mulai dari pangkat tertinggi ke terendah pada sebuah bagan. Selanjutnya, melakukan operasi hitung perkalian dan penjumlahan hingga mendapatkan nilainya.
Misalkan suku banyak berderajat empat dinyatakan dalam bentuk umum berikut.
f(x) = a4x4 + a3x3 + a2x2 + a1x + a0
Bentuk bagan dan letak koefisien sesuai aturan yang telah ditentukan dapat dilihat pada gambar di bawah.

Baca Juga: Contoh Soal Kesamaan Suku Banyak
Berikut ini adalah langkah-langkah detailnya untuk menentukan nilai dari suku banyak f(x) berderajat 4 dengan bentuk umum seperti persamaan di atas dengan cara skema.
Pertama: buat skema/bagan dan letakkan koefisien dari suku banyak f(x) sesuai aturan.
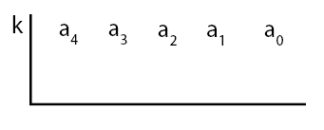
Ke dua: lakukan operasi perkalian dan penjumlahan dengan langkah sebagai berikut.

Keterangan: tanda anak panah merah menujukkan tidak ada proses yang perlu dilakukan, sedangkan tanda anak panah biru menunjukkan proses perkalian.
Ke tiga: menentukan nilai suku banyak
Nilai dari suku banyak f(x) untuk x = k adalah f(k) = a0+ a1k + a2k2 + a3k3 + a4k4.
Untuk membantu pemabahan sobat, perhatikan proses pengerjaan menentukan nilai f(x) di titik x = k dengan cara horner berikut.
Soal:
Tentukan nilai suku banyak f(x) = x3+ 3x2 + 4x ‒ 1 untuk x = 2 dengan cara skema!
Jawab:
Perhatikan gambar skema yang sesuai dengan f(x) = x3+ 3x2 + 4x ‒ 1 di bawah!

Sehingga, nilai suku banyak $f(x) = x^{3} + 3x^{2} + 4x – 1$ untuk x = 2 adalah 27.
Baca Juga: Teorema Sisa dan Teorema Faktor pada Suku Banyak (Polinomial)
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Nilai Suku Banyak untu Suatu Nilai x
Nilai dari f(x) = x2 + 4x ‒ 16 untuk x = 4 adalah ….
A. 16
B. 23
C. 38
D. 40
E. 56
Pembahasan:
Substitusi nilai x = 4 pada persamaan f(x):
f(x) = x2 + 4x ‒ 16
f(x) = 42 + 4(4)‒ 16
f(x) = 16 + 16 ‒ 16 = 16
Nilai dari f(x) = x2 + 4x ‒ 16 untuk x = 4 adalah f(x) = 16.
Jawaban: A
Contoh 2 – Soal Nilai Suku Banyak untu Suatu Nilai x
Diketahui nilai f(3) = 46 dan f(x) = 2x4 + x3 ‒ 3x2 ‒ kx + k maka nilai k adalah ….
A. 19
B. 24
C. 39
D. 43
E. 58
Pembahasan:
Substitusi nilai x = 3 pada persamaan f(x):
f(x) = 2x4 + x3 ‒ 3x2 ‒ kx + k
f(3) = 2(3)4 + (3)3 ‒ 3(3)2 ‒ k(3) + k
46 = 2 ∙ 81 + 27 ‒ 272 ‒ 3k + k
46 = 162 ‒ 2k
2k = 162 ‒ 46 = 116
k = 116/2 = 58
Jawaban: E
Sekian pembahasan mengenai pengertian suku banyak dan cara menentukan nilai suku banyak pada suatu nilai x. Jika ada bagian yang tidak paham bisa ditanyakan pada kolom komentar. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Operasi Suku Banyak: Penjumlahan, Pengurangan dan Perkalian

