PK atau Pengetahuan Kuantitatif menjadi salah satu tubtes UTBK. Merupakan bagian dari Tes Potensi Skolastik (TPS). Ada 10 contoh soal PK UTBK 2023 di halaman simulasi-tes.bppp.kemdikbud.go.id. Salinan dari sepuluh contoh soal PK UTBK 2023 dan pembahasannya ada di bawah.
Daftar isi:
- Contoh Soal PK UTBK 2023 No 1
- Contoh Soal PK UTBK 2023 No 2
- Contoh Soal PK UTBK 2023 No 3
- Contoh Soal PK UTBK 2023 No 4
- Contoh Soal PK UTBK 2023 No 5
- Contoh Soal PK UTBK 2023 No 6
- Contoh Soal PK UTBK 2023 No 7
- Contoh Soal PK UTBK 2023 No 8
- Contoh Soal PK UTBK 2023 No 9
- Contoh Soal PK UTBK 2023 No 10
Baca juga: Rekomendasi Buku UTBK 2025 Terbaik untuk Persiapanmu!
Contoh Soal PK UTBK 2023 No 1
Bilangan berikut yang habis dibagi 3 tetapi tidak habis dibagi 5 adalah ….
(A) 12345
(B) 13689
(C) 14670
(D) 15223
(E) 20579
Jawab: (B)
Akan dicari bilangan yang habis dibagi tiga dan TIDAK habis dibagi tiga.
Pertama, eliminasi bilangan yang habis dibagi 5. Bilangan yang habis dibagi 5 selalu berakhir dengan 0 atau 5. Maka bilangan 12345 dan 14670 bukan jawabannya,
Tersisa tiga bilangan yang bisa menjadi jawabannya yaitu 13689, 15223, dan 20579. Ciri bilangan habis dibagi tiga adalah jumlah angka pembentuknya merupakan kelipatan 3.
Jumlah bilangan:
13689 = 1 + 3 + 6 + 8 + 9 = 27
15223 = 1 + 5 + 2 + 2 + 3 = 13
20579 = 2 + 0 + 5 + 7 + 9 = 23
Dari nilai 27, 13, dan 23. Hanya 27 yang dapat habis dibagi 3. Jadi, bilangan berikut yang habis dibagi 3 tetapi tidak habis dibagi 5 adalah 13689.
Contoh Soal PK UTBK 2023 No 2
Kurva y = ax2 + 2x + 1 dengan a ≠ 0 memotong sumbu-x di dua titik berbeda. Pernyataan yang benar adalah …
(A) a < 1
(B) 6a < 1
(C) a > 1
(D) 3a > 1
(E) 3a > 2
Jawab: (A)
Untuk mengerjakan soal ini, kamu perlu tahu bahwa nilai diskriminan D = b2 – 4ac menentukan banyak titik potong kurva dengan sumbu x.
Ketentuan:
1) D > 0 → memiliki dua titik potong
2) D = 0 → memiliki satu titik potong
3) D < 0 → tidak memiliki titik potong
Persamaan y = ax2 + 2x + 1 merupakan persamaan kuadrat. Syarat persamaan kuadrat memotong sumbu x di dua titik adalah memiliki nilai diskriminan lebih dari nol (D = b2 ‒ 4ac > 0).
Nilai diskriminan (D) fungsi y = ax2 + bx + c adalah D = 22 ‒ 4(a)(1) = 4 ‒ 4a. Sehingga, syarat kurva y = ax2 + 2x + 1 memotong sumbu-x di dua titik adalah 4 ‒ 4a > 0.
Menentukan nilai a:
4 ‒4a > 0
‒4a > ‒4
Jadi, pernyataan yang benar adalah a < 1 (A).
Contoh Soal PK UTBK 2023 No 3
Kurva y = ax2 + 2x + 1 dengan a ≠ 0 memotong sumbu-x di dua titik berbeda. Pernyataan yang benar adalah ….
(A) kurva terbuka ke atas
(B) kurva terbuka ke bawah
(C) kurva memotong sumbu-y positif
(D) kurva memotong sumbu-y negatif
(E) titik punvak kurva berada di kuadran I
Jawab: (C)
Ketentuan sketsa grafik fungsi kuadrat dapat digunakan untuk mengerjakan soal ini. Ketentuan-ketentuannya seperti berikut.
Nilai a menentukan arah terbuka parabola:
1) a > 0 → parabola terbuka ke atas
2) a < 0 → parabola terbuka ke bawah
3) a = 0 → grafik tidak berupa parabola
Fungsi y = ax2 + 2x + 1 memotong sumbu-x di dua titik berbeda. Dicapai saat nilai a < 1. Nilai a dapat positif atau negatif sehingga bentuk kurva dapat terbuka ke atas atau ke bawah.
Nilai ab menentukan letak koordinat titik balik kurva parabola
1) ab > 0 → titik balik di kiri sumbu y
2) b = 0 → titik balik terletak pada sumbu y
3) ab < 0 → titik balik terletak di kanan sumbu y
Nilai a < 1 dan b = 2, sehingga ada dua kemungkinan nilai ab. Yaitu ab > 0 saat 0 < a < 1 dan ab < 0 saat a < 0. Maka letak titik puncak kurva tidak diketahui secara pasti.
Nilai c menentukan letak titik potong dengan sumbu y
1) c > 0 → memotong sumbu y positif
2) c = 0 → memotong sumbu y pada ordinat y = 0
3) c < 0 → memotong sumbu y negatif
Nilai c dari fungsi y = ax2 + 2x + 1 adalah c = 1, sehingga nilai c > 0. Untuk nilai c > 0, kurva memotong sumbu-y positif. Jadi, pernyataan yang benar adalah kurva memotong sumbu-y positif.
Contoh Soal PK UTBK 2023 No 4
Persamaan garis:
(1) y = ‒x + 5
(2) y = x ‒ 2
(3) y = 3x ‒ 1
(4) y = ‒2x + 7
Garis dengan persamaan mana saja yang memotong garis 2x + y = 4 dan x + 2y = 2 di dua titik berbeda?
(A) (1), (2), dan (3) SAJA yang benar
(B) (1) dan (3) SAJA yang benar
(C) (2) dan (4) SAJA yang benar
(D) HANYA (4) yang benar
(E) SEMUA pilihan benar
Jawab: (B)
Dua garis saling berpotongan jika memiliki nilai gradien garis berbeda.
Rumus gradien garis:
Gradien garis 2x + y = 4 tidak sama dengan gradien garis x + 2y = 2. Artinya, kedua garis memiliki titik potong. Koordinat titik potong garis 2x + y = 4 dan x + 2y = 2 adalah solusi dari sistem persamaan linear dua variabel (SPLDV).
Elimnasi x untuk mendapat nilai y:
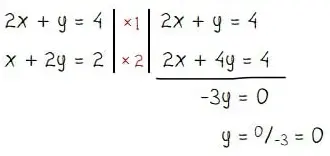
Substitusi nilai y = 0 ke persamaan 2x + y = 4 untuk mencari nilai x:
2x + 0 = 4
2x = 4
Titik potong garis garis 2x + y = 4 dan x + 2y = 2 adalah (2, 0).
Analisis Jawaban
Sebuah garis akan memotong garis 2x + y = 4 dan x + 2y = 2 di dua titik ketika memenuhi kondisi-kondisi berikut.
- Gradien garis tidak sama dengan –2 atau 1/2
- Tidak melalui titik potong kedua garis
Menentukan gradien garis persamaan (1) sampai (4):
| Persamaan | Nilai Gradien |
| y = ‒x + 5 | m = ‒1 |
| y = x ‒ 2 | m = 1 |
| y = 3x ‒ 1 | m = 3 |
| y = ‒2x + 7 | m = ‒2 |
Dari empat nilai gradien, persamaan garis (4) y = ‒2x + 7 memiliki gradien yang sama dengan garis 2x + y = 4 yaitu m = ‒2. Sehingga persamaan (4) tidak memotong garis pada dua titik dengan garis 2x + y = 4 dan x + 2y = 2.
Selanjutnya perlu diselidiki ketiga garis tersisa. Apakah letak titik potong dari garis-garis berada di perpotongan kedua garis atau tidak.
Untuk garis (1) y = ‒x + 5:
2x + y = 4
2x + (‒x + 5) = 4
x = 4 ‒ 5 = ‒1
y = ‒x + 5 = ‒(‒1 ) + 5 = 6
Salah satu titik potongnya adalah (‒1, 6).
Untuk garis (2) y = x ‒ 2:
2x + y = 4
2x + (x ‒ 2) = 4
3x = 4 + 2 = 6
x = 6/3 = 2
y = x ‒ 2 = 2 ‒ 2 = 0
Salah satu titik potongnya adalah (2, 0).
Untuk garis (3) y = 3x ‒ 1:
2x + y = 4
2x + (3x ‒ 1) = 4
5x = 4 + 1 = 5
Sehingga,
y = 3x ‒ 1 = 3 ‒ 1 = 2
Salah satu titik potongnya adalah (1, 2).
Persamaan garis (2) memiliki satu titik potong yang sama dengan titik potong kedua garis yaitu (2, 0). Sedangkan persamaan garis (1) y = ‒x + 5 dan (3) y = 3x ‒ 1 memiliki titik potong berbeda dengan titik potong kedua garis.
Jadi, persamaan garis yang memotong garis 2x + y = 4 dan x + 2y = 2 di dua titik berbeda adalah garis (1) y = ‒x + 5 dan (3) y = 3x ‒ 1.
Contoh Soal PK UTBK 2023 No 5
Diberikan kumpulan data 3, 5, 7, a
Berapakah banyaknya dari empat pernyataan berikut yang bernilai benar berdasdarkan informasi di atas?
(1) Rata-rata kumpulan data tersebut 6 bila a = 9
(2) Median kumpulan data tersebut 5 bila a = 7
(3) Jangkauan kumpulan data tersebut 4 bila a = 6
(4) Modus kumpulan data tersebut 3 bila a = 5
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Jawab: (C)
Pengertian rata-rata, median, jangkauan, dan modus:
Rata-rata: menjumlahkan semua nilai data dan kemudian membagi dengan banyak data.
Data: 3, 5, 7, 9
Median: nilai tengah dari data yang sudah diurutkan
Data yang telah diurutkan: 3, 5, 7, 9
Jangkauan: selisih nilai terbesar dan terkecil
Data: 3, 5, 7, 6
Data terurut: 3, 5, 6, 7
Jangkauan = 7 ‒ 3 = 4
Modus: nilai dengan frekuensi tertinggi atau nilai yang sering muncul
Data: 3, 5, 7, 5
Frekuensi untuk nilai 3, 5, dan 7 berurut-turut adalah 1, 2, dan 1
Modus = 5
Jadi, banyaknya empat pernyataan yang bernilai benar berdasdarkan informasi di atas adalah 2 yaitu rata-rata = 6 dan jangkauan = 4.
Contoh Soal PK UTBK 2023 No 6
Tiga bola diambil dari sebuah kotak yang berisi 3 bola merah dan 2 bola putih. Misalkan B menyatakan kejadian terambilnya 2 bola merah dan 1 bola putih dan P(B) menyatakan peluang kejadian B.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?
| P | Q |
| P(B) | 3/10 |
(A) P > Q
(B) Q > P
(C) P = Q
(D) Tidak dapat ditentukan hubungan
Jawab: (A)
Cari tahu nilai P(B) terlebih dahulu dari informasi berikut.
Banyak bola
Merah: n(Merah) = 3
Putih: n(Putih) = 2
Jumlah bola: n = 3 + 2 = 5
Banyak cara mengambil bola (gunakan rumus kombinasi):
2 bola merah dari 3 bola merah:
1 bola merah dari 2 bola putih:
3 bola dari 5 bola dalam kotak:
Besar peluang kejadian A (terambilnya 2 bola merah dan 1 bola putih):
Diperoleh nilai P = P(B) = 3/5 = 0,6 dan Q = 3/10 = 0,3 jadi dapat disimpulkan hubungan P > Q.
Contoh Soal PK UTBK 2023 No 7
Bilangan real x memenuhi pertidaksamaan 2x + 1 < 4.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?
| P | Q |
| ‒2x | 2 |
(A) P > Q
(B) Q > P
(C) P = Q
(D) Tidak dapat ditentukan hubungan
Jawab: (D)
Untuk menentukan hubungan antara P = ‒2x dan Q = 2 perlu diketahui nilai x terlebih dahulu. Cara menentukan nilai x yang memenuhi pertidaksamaan 2x + 1 < 4 dapat dilakukan seperti berikut.
2x + 1 < 4
2x < 4 ‒ 1
x < 3/2
Dari hasil perhitungan diperoleh nilai x yang memenuhi pertidaksamaan 2x + 1 < 4 adalah x < 3/2. Di mana untuk nilai x < 3/2 dapat membuat nilai 2x bernilai lebih dari, kurang dari, atau sama dengan 2. Jadi, hubungan antara kuantitas P dan Q adalah tidak dapat ditentukan hubungan.
Contoh Soal PK UTBK 2023 No 8
Titik P dan Q berturut-turut terletak pada rusuk AB dan BC kubus ABCD.EFGH dengan PA : PB = 1 : 2 dan BQ : QP = 1 : 1. Manakah dari tiga pernyataan berikut yang bernilai benar berdasarkan informasi di atas?
- Perbandingan volume limas PBQ.F dan volume kubus ABCD.EFGH = 1 : 18
- Perbandingan luas ΔPBQ dengan luas persegi ABCD = 1: 16
- PQ : AC = 1 : √2
(A) Semua pernyataan benar
(B) Pernyataan (1) dan (2) SAJA yang benar
(C) Pernyataan (2) dan (3) SAJA yang benar
(D) Pernyataan (3) SAJA yang benar
(E) Tidak ada penyataan yang benar
Jawab: (B)
Misalkan panjang rusuk kubus adalah s. Gambar kubus dan limas beserta keterangannya nampak seperti berikut.

Selanjutnya, tiga pernyataan yang diketahui dapat diselidiki satu per satu.
Volume kubus dan limas
Volume kubus:
Vkubus = s × s × s
Vkubus = s3
Volume limas: Vlimas = ⅓ × Lalas × t
Vlimas = 1/3 × (1/2 × 2/3 s × 1/2s) × s
Vlimas = 1/3 × 2/12s × s = 1/18s3
Perbandingan volume kubus dan limas:
Luas segitiga PBQ dan persegi ABCD
Luas segitiga PBQ:
LΔPBQ = ½ × ⅔s × ½s
LΔPBQ = 1/6s2
Luas persegi ABCD:
LABCD = s × s
LABCD = s2
Perbandingan ΔPBQ dengan luas persegi ABCD:
LΔPBQ : LABCD = 1/6s2 : s2
LΔPBQ : LABCD = 1/6 : 1 = 1 : 6
Panjang PQ dan QC
Untuk perbandingan panjang PQ dan QC dapat diketahui melalui penyelesaian berikut.

Jadi, jawabannya adalah pernyataan (1) dan dan (2) SAJA yang benar.
Contoh Soal PK UTBK 2023 No 9
Diketahui segitiga ABC dengan ∠B = 30o. Apakah segitiga ABC siku-siku? Putuskan apakah peernyataan (1) dan (2) berikut cukup untuk menjawab pertanyaan tersebut.
1. ∠A ‒ ∠C = 20o
2. ∠C = ∠A
(A) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
(B) Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
(C) Pernyataan (1) dan (2) cukup untuk menjawab pertanyaan, tetapi salah satu dari keduanya tidak cukup.
(D) Pernyataan (1) atau pernyataan (2) SAJA sudah cukup untuk menjawab pertanyaan.
(E) Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
Jawab: A
Diketahui bahwa besar ∠B = 30o sehingga besar sudut ∠A + ∠C = 180o ‒ 30o= 150o. Sementara untuk besar ∠A ‒ ∠C = 20o.
Segitiga siku-siku adalah sebuah segitiga yang memiliki besar sudut 90o pada salah satu sisinya. Diketahui bahwa besar ∠B = 30o, artinya besar dua sudut lainnya adalah 90o dan 60o.
INGAT:
Jumlah sudut dalam segitiga adalah 180o. Sehingga selisih antara besar ∠A dan ∠C sama dengan ∠A ‒ ∠C = 30o.
Dari pernyataan (1) diberikan informasi bahwa ∠A ‒ ∠C = 20o yang dapat menjawab pertanyaan bahwa segitiga ABC bukan merupakan segitiga siku-siku.
Sementara pernyataan (2) diberikan informasi bahwa ∠C < ∠A yang tidak dapat digunakan untuk menjawab pertanyaan apakah segitiga ABC merupakan segitiga siku-siku. Di mana besar ∠C < ∠A tidak memberikan informasi yang menjelaskan mengenai segitiga siku-siku.
Kesimpulan: Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
Contoh Soal PK UTBK 2023 No 10
Diketahui b = 2c dan b ‒ d = 3. Apakah d bilangan prima? Putuskan apakah pernyataan (1) dan (2) berikut cukup untuk menjawab pernyataan tersebut.
1. d = 2c ‒ 3
2. b ‒ 2c = 0
(A) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
(B) Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
(C) Pernyataan (1) dan (2) cukup untuk menjawab pertanyaan, tetapi salah satu dari keduanya tidak cukup.
(D) Pernyataan (1) atau pernyataan (2) SAJA sudah cukup untuk menjawab pertanyaan.
(E) Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
Jawab: (E)
Diketahui b = 2xc dan b ‒ d = 3 dan penyataan (1) d = 2c ‒ 3 dan (2) b ‒ 2c = 0.
Penyataan (1): d = 2c ‒ 3
Sementara diketahui b ‒ d = 3 atau d = b ‒ 3 = 2xc ‒ 3
Pernyataan (2): b ‒ 2c = 0 atau b = 2c
Sementara dari informasi yang diketahui pada soal adalah b = 2xc.
Diperoleh sistem persamaan yang terdiri dari 2 persamaan dan 3 variabel, serta persamaan yang tidak konsisten. Sehingga dapat ditarik kesimpulan: Penyataan (1) dan (2) tidak cukup untuk menjawab pertanyaan.
Itulah 10 contoh soal PK UTBK 2023 dari halaman simulasi-tes.bppp.kemdikbud.go.id dengan pembahasan soal yang diperjelas. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
