Banyaknya susunan kata berbeda yang dapat dibentuk dari huruf-huruf penyusun suatu kata dapat ditentukan melalui n faktorial. Notasi faktorial adalah operasi hitung bilangan dengan mengalikan bilangan-bilangan dari n sampai satu, di mana n adalah bilangan yang difaktorialkan. Misalnya 3 faktorial yang dituliskan 3! akan sesuai dengan nilai 3! = 3×2×1 = 6. Jika dalam kata terdapat beberapa huruf yang sama maka digunakan rumus permutasi n unsur dengan r unsur yg sama.
Tiga buah huruf yang terdiri dari A, I, dan R dapat membentuk kata AIR, ARI, IAR, IRA, RIA, dan RAI. Sehingga banyaknya susunan kata berbeda yang dapat dibentuk dari huruf penyusun kata AIR ada sebanyak 6 cara. Susunan kata yang dibentuk dapat memiliki arti atau tidak juga memiliki arti.

Cara menentukan banyaknya susunan kata berbeda dari huruf-huruf yang menyusun suatu kata dengan cara mendaftarnya seperti di atas tentu tidak efisien. Sehingga dibutuhkan cara yang lebih baik untuk menentukan banyak susunan kata dari huruf-huruf penyusun suatu kata. Di awal sudah disebutkan bahwa caranya dapat menggunakan notasi faktorial dan rumus permutasi n unsur berbeda dengan beberapa unsur yang sama.
Bagaimana cara menentukan banyaknya susunan kata berbeda yang dapat dibentuk dari huruf-huruf penyusun suatu kata? Bagaimana penggunaan rumus permutasi n unsur dengan beberapa unsur yang sama? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Notasi Faktorial dan Cara Melakukan Perhitungannya
- Rumus Permutasi n Unsur dengan Beberapa Unsur Sama
- Contoh Soal dan Pembahasan
Baca Juga: Perbedaan Permutasi dan Kombinasi
Notasi Faktorial dan Cara Melakukan Perhitungannya
Sebelum ke pembahasan cara menentukan banyaknya susunan kata berbeda dari suatu kata, ingat kembali bagaimana cara menihitung bilangan dengan notasi faktorial.
Notasi faktorial adalah sebuah notasi yang digunakan untuk menyatakan persamaan perkalian urutan bilangan-bilangan bulat positif. Sebagai contoh perkalian 8 bilangan bulat positif berurutan dituliskan dengan 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 8!. Secara umum, rumus umum bilangan n faktorial memenuhi persamaan n! = n × (n×1) × … × 1.

Contoh penggunaan notasi faktorial digunakan untuk menentukan banyaknya susunan n objek yang berbeda. Misalnya, terdapat 5 obyek berbeda maka banyaknya susunan yang dapat dibentuk sama dengan 5! = 5 × 4 × 3 × 2 × 1 = 120 kata.
Contoh lain, penggunaan notasi faktorial digunakan untuk menentukan banyak susunan kata yang dibentuk dari huruf-huruf yang semuanya berbeda misalnya SERING. Kata sering tersusun oleh 6 huruf berbeda, sehingga banyaknya susunan kata berbeda yang dapat dibentuk sama dengan 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720 kata.

Baca Juga: Contoh Soal Duduk Melingkar dan Pembahasannya
Rumus Permutasi n Unsur dengan Beberapa Unsur Sama
Suatu kata sering juga memiliki beberapa huruf yang sama, misalnya pada kata MATEMATIKA. Di dalam kata tersebut terdapat 10 huruf yang terdiri dari 2 huruf M, 3 huruf A, 2 huruf T, 1 huruf E, 1 huruf I, dan 1 huruf K. Ada tiga huruf yang muncul lebih dari satu (obyek sama) dan tiga huruf yang muncul hanya sekali dalam KATAMATEMATIKA.
Pada persoalan seperti kata MATEMATIKA, banyak susunan kata berbeda dapat ditentukan dengan rumus permutasi n unsur dengan beberapa obyek berbeda.

Perhatikan bagaimana penggunaan rumus permutasi di atas untuk menyelesaiakan contoh soal berikut.
Contoh:
Tentukan banyaknya susunan kata berbeda yang dapat dibentuk dari huruf-huruf penyusun kata MATEMATIKA!
Penyelesaian:
Pada kata MATEMATIKA seluruhnya terdapat sebanyak 10 huruf yang terdiri dari dua huruf M, tiga huruf A, dua huruf T, satu huruf E, satu huruf I, dan satu huruf K. Jadi, banyaknya susunan kata berbeda yang dapat dibentuk dari huruf-huruf penyusun kata MATEMATIKA dapat dihitung seperti penyelesaian berikut.

Baca Juga: Peluang Kejadian Majemuk dan Bersyarat
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Banyaknya Susunan Kata Berbeda
Banyak susunan kata berbeda yang dapat dibentuk oleh huruf-huruf penyusun kata JAKARTA adalah . . . kata.
A. 840
B. 560
C. 360
D. 180
E. 90
Pembahasan:
Huruf-huruf penyusun kata JAKARTA adalah J (1 huruf), A (3 huruf), K (1 huruf), R (1 huruf), dan T (1 huruf). Huruf-huruf yang menyusun kata JAKARTA ada sebanyak 7 huruf dengan satu huruf muncul sebanyak tiga kali dan empat huruf muncul masing-masing satu kali.
Banyaknya susunan kata berbeda yang dapat dibentuk oleh huruf-huruf penyusun JAKARTA dapat dihitung seperti pada penyelesaian berikut.
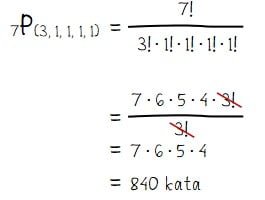
Jadi banyaknya susunan kata berbeda yang dapat dibentuk oleh huruf-huruf penyusun JAKARTA adalah 840 kata.
Jawaban: A
Contoh 2 – Banyaknya Susunan Kata Berbeda
Banyak susunan kata dengan huruf pertama berupa konsonan yang dapat dibentuk dari kata BUDAYA adalah . . . .
A. 60
B. 90
C. 120
D. 150
E. 180
Pembahasan:
Banyaknya huruf yang menyusun kata BUDAYA adalah 6 huruf yang meliputi 1 huruf B, 1 huruf U, 1 huruf D, 2 huruf A, dan 1 huruf Y. Huruf konsonan dari kata BUDAYA ada sebanyak 3 huruf yang terdiri dari B, D, dan Y.

Jadi, Banyak susunan kata dengan huruf pertama berupa konsonan yang dapat dibentuk dari kata BUDAYA adalah 180.
Jawaban: E
Contoh 3 – Banyaknya Susunan Kata Berbeda
Jika huruf-huruf K, A, M, I, dan S akan disusun secara alfabetis, maka kata KAMIS akan berada pada urutan ke ….
A. 12
B. 25
C. 51
D. 101
E. 120
Pembahasan:
Kata urutan pertama yang disusun secara alfabetis dari huruf K, A, M, I, dan S adalah AIKMS. Selanjutnya kata pada urutan kedua yang disusun secara alfabetis dari huruf K, A, M, I, dan S adalah AKIMS. Sementara urutan yang terakhir dari kata yang disusun dari lima huruf tersebut adalah SMKIA.
Banyaknya susunan yang dapat dibentuk oleh lima huruf berbeda adalah 5! = 5×4×3×2×1 = 120 susunan.
Semua kata berawalan K akan terbentuk pada urutan setelah semua susunan kata dengan awalan A dan I.
- Banyak kata berawalan A yang disusun dari huruf K, A, M, I, dan S:
= 1 × 4!
= 1 × 4 × 3 × 2 × 1
= 24 susunan
- Banyak kata berawalan I yang disusun dari huruf K, A, M, I, dan S:
= 1 × 4!
= 1 × 4 × 3 × 2 × 1
= 24 susunan
Urutan huruf yang pertama disusun berawalan huruf K secara alfabetis berturut-turut adalah KAIMS, KAISM, KAMIS, dan seterusnya. Sehingga urutan kamis KAMIS berada pada urutan ke-3 dari semua kata yang berawalan K.
Jadi, kata KAMIS akan berada pada urutan ke-(24 + 24 + 3) = 51.
Jawaban: C
Demikianlah tadi ulasan banyaknya susunan kata berbeda yang dapat dibentuk dari huruf-huruf penyusun suatu kata. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Aturan Pengisian Tempat (Filling Slots)
