Beda potensial antara titik A dan B sama dengan jumlah tegangan antara kedua titik tersebut. Rumus beda potensial pada rangkaian listrik adalah V = I × R. Untuk mengetahui nilai beda potensial perlu besaran kuat arus dan hambatan. Lebih lanjut mengenai cara menghitung beda potensial antara dua titik pada rangkaian listrik ada di bawah.
Daftar isi:
Baca Juga: Rangkaian Listrik Seri, Paralel, dan Campuran
Rumus Beda Potensial
Beda potensial sering disebut dengan tegangan (voltase). Satuan beda potensial dinyatakan dalam volt dan simbolnya adalah V.
Rumus beda potensial pada suatu rangkaian listrik adalah V = I × R. Keterangan I = kuat arus yang mengalir dan R = hambatan.
Contoh cara menghitung beda potensial ada pada penyelesaian soal di bawah.
Soal:
Arus listrik sebesar 5 A mengalir melalui sebuah rangkaian listrik yang memiliki hambatan 8 ohm. Tentukan beda potensial pada rangkaian listrik tersebut!
Jawab:
Diketahui besar kuat arus I = 5 A dan hambatan R = 8 ohm.
Sehingga,
V = I × R
V = 5 × 8 = 4 volt
Jadi, beda potensial pada rangkaian listrik tersebut adalah 8 volt.
Untuk tegangan antara dua titik, misalkan antara titik A dan B, besarnya adalah VAB. Besarnya sama dengan jumlah tegangan antara kedua titik tersebut. Sebelumnya, perlu juga untuk mengetahui Hukum Kirchoff yang ada pada bahasan di bawah.
Hukum Kirchoff
Hukum Kirchhoff menerangkan jumlah arus listrik dan beda potensial pada sebuah rangkaian listrik. Tokoh yang mengenalkan hukum Kirchoff ini adalah Gustav Robert Kirchhoff. Ada dua hukum Kirchoff yaitu Hukum I Kirchoff dan Hukum II Kirchoff. Bunyi hukumnya ada di bawah.
Hukum I Kirchoff
Bunyi:
Jumlah kuat arus yang masuk dalam titik percabangan sama dengan jumlah kuat arus yang keluar dari titik percabangan.
∑Imasuk = ∑Ikeluar
Sebagi contoh, terdat tiga arus masuk percabangan yaitu I1, I2, dan I3 serta sebuah arus keluar I. Persamaan yang sesuai untuk titik percabangan ini adalah I1 + I2 + I3 = I.
Hukum II Kirchoff
Bunyi:
Pada rangkaian tertutup jumlah aljabar GGL (ε) dan jumlah penurunan potensial (IR) sama dengan nol. Atau total beda potensial (tegangan) pada suatu rangkaian tertutup adalah nol.
∑ε + ∑IR = 0
Keterangan:
∑ε = jumlah ggl sumber arus (volt)
∑IR = jumlah tegangan (volt)
I = kuat arus listrik (A)
R = hambatan (Ω, dibaca ohm)
Cara menggunakan Hukum II Kirchoff:
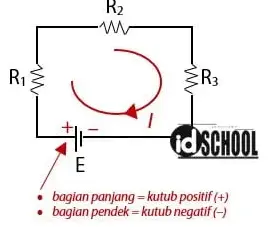
Pertama, buat perumpamaan arah kuat arus dan perumpamaan arah loop. Berlawanan arah jarum jam atau searah.
Kedua, bentuk persamaan mengikuti pemisalan loop yang telah dibuat pada langkah pertama. Ketentuannya mengikuti aturan berikut.
- Loop bertemu hambatan dalam (GGL) dari kutub positif maka nilainya positif.
- Loop bertemu GGL dari kutub negatif diberi tanda negatif.
- Saat loop bertemu hambatan menggunakan rumus V = IR
Perhatikan sebuah contoh menggunakan hukum II Kirchoff di bawah.
Titik mulai loop bisa dimulai dari mana saja. Misalkan loop dimulai dari arus yang melewati R1. Pertama diperoleh tegangan IR1 kemudian loop berlanjut ke hambatan R2 menghasilkan V = IR2.
Selanjutnya loop bertemu hambatan R3 menghasilkan V = IR3. Terakhir, loop bertemu sumber tegangan dari kutub negatif sehingga nilanya – E.
Persamaan yang sesuai untuk rangkaian listrik tertutup tersebut adalah IR1 + IR2 + IR3 – E = 0. Saat nilai-nilai hambatan diketahui, besar kuat arus yang mengalir pada rangkaian listrik dapat diketahui.
Baca Juga: Cara Hitung Biaya Pemakaian Listrik dan Contoh Soalnya
Contoh Soal dan Pembahasan
Rumus beda potensial dan hukum Kirchoff di atas berguna untuk menentukan besar beda potensial antara dua titik. Bagaimana cara menggunakannya terdapat pada contoh penyelesaian soal-soal di bawah.
Contoh 1 – Beda potensial antara dua titik
Perhatikan gambar rangkaian listrik berikut!
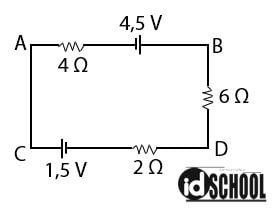
Beda potensial antara titik B dan D adalah ….
A. 0,5 V
B. 1 V
C. 3 V
D. 4 V
E. 8 V
Pembahasan:
Misalkan loop pada rangkaian listrik tertutup pada soal searah arah jarum jam. Ambil titik A sebagai awal arus listrik maka diperoleh persamaan berikut.

Menghitung arus listrik:
4I – 4,5 + 6I + 2I – 1,5 = 0
4I + 6I + 2I = 4,5 + 1,5
12I = 6
Menghitung VBD:
V = IR
VBD = 0,5 × 6 = 3 V
Jadi, beda potensial antara kedua titik tersebut adalah 3 V.
Jawaban: C
Baca Juga: Pengaruh Rangkaian GGL Seri dan Paralel Terhadap Besar Kuat Arus
Contoh 2 – Beda potensial antara titik A dan B
Perhatikan gambar rangkaian listrik berikut ini!
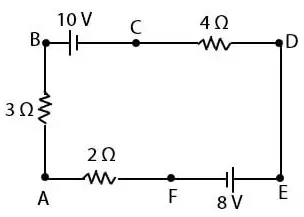
Beda potensial antara titik A dan B adalah ….
A. 1,5 volt
B. 3,0 volt
C. 6,0 volt
D. 7,5 volt
E. 9,0 volt
Pembahasan:
Misalkan arah loop searah arah jarum jam. Ambil titik A sebagai awal arus listrik. Dengan mengikuti arah loop dapat dibentuk persamaan 3I + 10 + 4I + 8 + 2I = 0.
Sehingga,
9I + 18 = 0
9I = –18
Note: tanda minus menunjukkan arah pemisalah loop yang terbalik
Menghitung VAB:
VAB = I × RAB
VAB = 2 × 3 = 6 V
Jadi, beda potensial antara titik A dan B adalah 6 V.
Jawaban: C
Baca Juga: Rumus pada Medan Listrik dan Hukum Coulomb
Contoh 3 – Beda Potensial antara 2 titik
Perhatikan rangkaian listrik berikut!
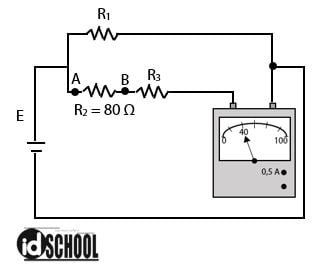
Beda potensial antara titik A dan B sebesar ….
A. 16 V
B. 32 V
C. 160 V
D. 320 V
E. 1.600 V
Pembahasan:
Langkah pertama menghitung arus listrik (I) yang mengalir pada rangkaian listrik. Caranya dengan membaca amperemeter yang terpasang.
Menghitung VAB:
VAB = I × RAB
VAB = 0,2 × 80 = 16 V
Jadi, beda potensial antara titik A dan B sebesar 16 V.
Jawaban: A
Sekian ulasan cara menghitung beda potensial antara titik A dan B. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Cara Membuat Benda Bermuatan Listrik Statis