Rumus Energi Potensial Kinetik dan Mekanik

Diketahui ada tiga macam energi yaitu energi potensial, energi kinetik, dan energi mekanik. Ketiga macam energi tersebut memiliki rumus yang berbeda untuk perhitungannya. Rumus energi potensial adalah Ep = m×g×h dan rumus energi kinetik adalah Ek =½×m×v². Sementara rumus energi mekanik sama dengan jumlah antara energi potensial dan energi kinetik sehingga memenuhi persamaan Em = Ep + Ek. Satuan ketiga macam energi yang telah disebutkan tadi sama yaitu Joule (J) atau Newton Meter (Nm).

Kata energi merupakan bahasa yunani yaitu kata ergon yang berarti kerja. Sedangkan pengertian energi dapat dipahami sebagai kemampuan untuk melakukan suatu tindakan atau usaha/pekerjaan. Energi potensial adalah besar energi yang dipengaruhi oleh letak ketinggian benda, sedangkan energi kinetik adalah besar energi yang dipengaruhi oleh gerak benda. Hubungan antara energi potensial dan kinetik pada suatu titik dinyatakan melalui energi mekanik yang selalu sama di setiap titik

Apa itu energi potensial? Apa itu energi kinetik dan mekanik? Bagaimanakah rumus energi potensial? Apa rumus untuk menghitung energi kinetik? Bagaimana cara menghitung besar energi mekanik? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Rumus Energi Potensial
  • Contoh Cara Menghitung Energi Potensial
• Rumus Energi Kinetik
  • Contoh Cara Menghitung Energi Kinetik
• Rumus Energi Mekanik = Energi Potensial + Energi Kinetik
  • Contoh Menghitung Energi Mekanik
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Penggunaan Rumus Energi Potensial
  • Contoh 2 – Soal Energi Kinetik
  • Contoh 3 – Soal Penerapan Rumus Energi Potensial dan Energi Kinetik

Rumus Energi Potensial

Energi potensial adalah energi yang dimiliki benda karena ketinggian dari kedudukan/posisi benda. Semakin tinggi posisi benda dari permukaan tanah, besar nilai energi potensial akan semakin besar. Begitu juga sebaliknya, besar nilai energi potensial akan semakin kecil ketika ketinggian benda semakin rendah.

Besar energi potensial akan maksimal saat berada pada ketinggian maksimal (h = h_max). Nilai besar energi potensial akan sama dengan nol jika posisi benda berada tepat diatas permukaan tanah (h = 0).

Selain tinggi benda, besar energi potensial juga dipengaruhi oleh massa benda (m) percepatan gravitasi bumi (g). Massa benda yang semakin berat akan membuat energi potensial yang dihasilkan semakin besar. Sebaliknya, massa benda yang semakin ringan akan membuat besar energi potensial semakin kecil.

Besar gravitasi bumi (g) mempunyai nilai rata-rata yang hampir sama pada setiap permukaan bumi yaitu g = 9,8 m/s² atau sering dibulatkan dengan g = 10 m/s². Sehingga, pengaruh gravitasi bumi tidak berpengaruh pada perbandingan energi potensial dua benda yang terletak di tempat berbeda dengan ketinggian yang sama.

Rumus energi potensial secara matematis dinyatakan melalui persamaan berikut.

Baca Juga: Pesawat Sederhana (Tuas, Katrol, dan Bidang Miring)

Contoh Cara Menghitung Energi Potensial

Soal:
Suatu benda yang bermassa 0,075 kg yang terlempar ke atas dengan ketinggian maksimum 1,4 m. Jika diketahui percepatan gravitasi adalah 10 m/s² maka besarnya energi potensial tersebut adalah … Joule.
A. 1,05
C. 3,5
B. 1,5
D. 0,05​

Penyelesaian:
Berdasarkan keterangan yang diberikan pada soal dapat diketahui beberapa nilai besaran seperti berikut.

• Massa benda: m = 0,075 kg
• Ketinggian maksimum: h = 1,4 m
• Percepatan gravitasi: g = 10 m/s²

Menghitung energi potensial:
Ep = m×g×h
Ep = 0,075×10×1,4 = 1,05 joule

Jadi, besarnya energi potensial pada benda tersebut adalah 1,05 joule. (B)

Baca Juga: Rumus Energi dan Daya Listrk

Rumus Energi Kinetik

Energi kinetik adalah energi yang dimiliki oleh benda karena geraknya. Setiap benda yang bergerak memiliki energi kinetik. Besar energi kinetik dipengaruhi oleh massa benda (m) dan kecepatan benda (v), begitu juga sebaliknya. Semakin tinggi kecepatan benda (v) akan membuat energi kinetik semakin besar, juga berlaku untuk kondisi sebaliknya.

Pada kasus benda yang jatuh pada ketinggian tertentu, besar nilai energi kinetik akan mencapai maksimal saat mencapai permukaan tanah. Kondisi ini dikarenakan benda akan memiliki kecepatan tertinggi sesaat sebelum tepat berhenti di atas permukaan tanah.

Sedangkan besar nilai energi kinetik paling kecil/minimal (sama dengan nol) saat benda tepat akan dijatuhkan. Hal ini dikarenakan benda pada awalnya tidak memiliki kecepatan (v_o = 0) sehingga energi kinetik akan sama dengan nol.

Rumus energi kinetik secara matematis sesuai dengan persamaan berikut.

Contoh Cara Menghitung Energi Kinetik

Soal:
Sebuah benda bermassa 60 kg bergerak dengan kecepatan 5 m/s. Besar energi kinetik benda tersebut adalah …. joule.
A. 125
B. 250
C. 625
D. 750

Penyelesaian:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh beberapa nilai besaran seperti berikut.

• Massa benda: m = 60 kg
• Kecepatan benda: v = 5 m/s

Menghitung besar energi kinetik benda:
Ek =½×m×v²
Ek =½×60×5²
= ½×60×25
= 750 joule

Jadi, besar energi kinetik benda tersebut adalah 750 joule. (D)

Baca Juga: Cara Menghitung Biaya Pemakaian Listrik

Rumus Energi Mekanik = Energi Potensial + Energi Kinetik

Energi mekanik merupakan jumlah energi dalam sebuah sistem mekanik. Terdapat sebuah hukum yang menyatakan bahwa Energi tidak dapat diciptakan dan tidak dapat dimusnahkan. Hukum tersebut dikenal sebagai Hukum Kekekalan Energi Mekanik. Besar energi mekanik pada setiap titik adalah sama.

Rumus energi mekanik secara matematis dapat dinyatakan seperti persamaan di bawah.

Contoh Menghitung Energi Mekanik

Soal:
Sebuah benda bermassa 2 kg jatuh dari ketinggian 1 m dengan kecepatan 5 m/s. Jjika diketahui percepatan gravitasi 10 m/s² maka besar energi mekanik benda adalah ….
A. 45 joule
B. 90 joule
C. 135 joule
D. 180 joule

Penyelesaian:
Beberapa informasi yang diberikan pada soal memuat nilai-nilai besaran seperti berikut.

• massa benda: m = 2 kg
• ketinggian: h = 1 m
• kecepatan benda: v= 5 m/s
• percepatan gravitasi: g = 10 m/s²

Menghitung besar energi potensial: Ep = m×g×h
Ep = 2×10×1
Ep = 20 joule

Menghitung besar energi kinetik: Ek = ½×m×v²
Ek = ½×2×5²
Ek = ½×2×25 = 25 joule

Jadi, besar energi menkanik pada benda tersebut adalah Em = Ep + Ek = 20 + 25 = 45 joule.

Baca Juga: Perbedaan Gaung dan Gema

Contoh Soal dan Pembahasan

Soal dapat melatih kemampuan memahami materi, termasuk untuk materi rumus energi potensial kinetik dan mekanik. Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk memperdalam pemahaman. Setiap contoh soal dilengkapi dengan pembahasan yang dapat digunakan sebagai tolak ukur keberhasilan mengerjakannya. Selamat berlatih!

Contoh 1 – Soal Penggunaan Rumus Energi Potensial

Perhatikan gambar berikut!

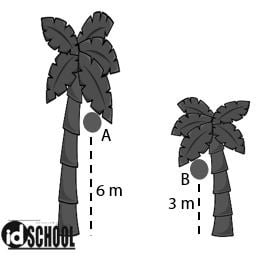
Massa buah kelapa A adalah 1,2 kg dan massa buah kelapa B adalah 1,8 kg. Jika percepatan gravitasi 9,8 m/s², perbandingan energi potensial buah kelapa A dan buah kelapa B adalah ….
A. 3 : 4
B. 4 : 3
C. 4 : 9
D. 9 : 4

Pembahasan:
Berdasarkan keterangan pada soal diperoleh informasi seperti berikut.

• Massa buah kelapa A: m_A = 1,2 kg
• Massa buah kelapa B: m_B = 1,8 kg
• Ketinggian buah kelapa A: h_A = 6 m
• Ketinggian buah kelapa B: h_B = 3 m
• Percepatan gravitasi: g = 9,8 m/s²

Menghitung energi potensial buah kelapa A:
Ep_A = m_A × g × h_A
= 1,2 × 9,8 × 6
= 70,56

Menghitung energi potensial buah kelapa B:
Ep_B = m_B × g × h_B
= 1,8 × 9,8 × 3
= 52,92

Jadi, perbandingan energi potensial buah kelapa A dan B adalah Ep_A : Ep_B = 70,56 : 52,92 = 4 : 3.

Jawaban: B

Contoh 2 – Soal Energi Kinetik

Pembahasan:
Berdasarkan keterangan pada soal diperoleh informasi seperti berikut.

• Percepatan gravitasi: g = 10 m/s²
• Massa buah kelapa: m = 2 kg
• Tinggi pohon kelapa pada titik A: h_A = 8 + 4 = 12 m
• Tinggi pohon kelapa pada titik B: h_B = 4 = 4 m

Ditanyakan: Ek pada titik B

Mencari energi potensial pada titik A:
Ep_A = m × g × h_A
Ep_A = 2 × 10 × 12 = 240 J

Menghitung energi mekanik:
Em = Ep_A + Ek_A
karena minimum, maka v = 0 sehingga Ek_A = 0
Em = 240 + 0
Em = 240 J

Menghitung energi kinetik di titik B: Em = Ep_B + Ek_B
Ek_B = Em – Ep_B
Ek_B = Em – (m × g × h)
= 240 – (2 × 10 × 4)
= 240 – 80 = 160 J

Jadi, energi kinetik yang di miliki buah kelapa sampai pada titik B sebesar 160 J.

Jawaban: C

Contoh 3 – Soal Penerapan Rumus Energi Potensial dan Energi Kinetik

Shania melakukan percobaan dengan menjatuhkan bola dari sebuah ketinggian.

Shania menyimpulkan perbandingan antara energi kinetik dan energi potensial pada titik C yaitu …. (g = 10 m/s²)
A. 3 : 2
B. 2 : 3
C. 1 : 4
D. 4 : 1

Pembahasan:
Berdasarkan keterangan pada soal diperoleh informasi seperti berikut.

• Kecepatan bola di titik A (saat dijatuhkan): v_a = 0
• Ketinggian bola di titik A: h_a = 5 m
• Ketinggian bola di titik C: h_c = 2 m
• Percepatan gravitasi bumi: g = 10 m/s²

Menghitung kecepatan bola pada titik C:
m × g × h_a + ½ × m × v_a² = m × g × h_c + ½ × m × v_c²
g × h_a + ½ × v_a² = g × h_c + ½ × v_c²
10 × 5 + 0 = 10 × 2 + ½ × v_c²
50 = 20 + ½v_c²
50 – 20 = 1/2 vc²
30 = ½ v_c²
60 = v_c²
v_c = √60 m/s

Menghitung perbandingan Ep dan Ek pada titik C:

Jadi, perbandingan antara energi kinetik dan energi potensial bola pada titik C yaitu 3 : 2.

Jawaban: A

Sekian bahasan rumus energi potensial, rumus energi kinetik, dan rumus energi mekanik. Bahasan juga dilengkapi penggunaan rumus untuk menyelesaikan beberapa contoh soal beserta pembahasannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Suhu Akhir Campuran