Suatu pernyataan majemuk dalam bahasan logika matematika memiliki bentuk ekuivalen pernyataan majemuk. Bentuk ekuivalen pernyataan majemuk dapat ditunjukkan melalui hasil nilai-nilai kebenaran yang sama. Contoh sederhana bentuk ekuivalen pernuataan majemuk terdapat pada Saya mampu mengerjakan soal matematika dan Saya bukan tidak mampu mengerjakan soal matematika. Kedua pernyataan tersebut terlihat berbeda. Namun, kedua pernyataan tersebut sebenarnya memiliki makna yang sama karena ada dua kali bentuk ingkaran atau negasi.
Contoh lain bentuk ekuivalen pernyataan majemuk: Jika saya pergi ke sekolah naik bus maka saya sampai sekolah tepat waktu dan Jika saya tidak sampai sekolah tepat waktu maka saya pergi ke sekolah tidak naik bus atau. Dua pernyataan tersebut merupakan pernyataan majemuk yang ekuivalen. Di mana prenyataan pertama merupakan implikasi dan pernyataan kedua merupakan bentuk kontraposisinya.

Ekuivalen secara umum dinyatakan dalam arti mempunyai nilai/ ukuran/ makna yang sama atau seharga. Kondisi ini bukan berarti bahwa ekuivalen dan sama dengan adalah hal yang sama. Pengertian sama dengan mengarah pada kondisi yang menunjukkan sama dan setara. Sedangkan ekuivalen memiliki cakupan kondisi yang lebih luas dari pengertian sama dengan.
Bagaimana cara mengetahui dua pernyataan majemuk yang saling ekuivalen? Bagaimana cara menentukan bentuk ekuivalen pernyataan majemuk? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Baca Juga: Konvers, Invers, dan Kontraposisi dari Suatu Implikasi
Pernyataan Majemuk yang Ekuivalen
Sebuah pernyataan majemuk bisa jadi memiliki lebih dari satu bentuk ekuivalen pernyataan majemuk. Perhatikan kembali contoh pernyataan majemuk: Jika saya pergi ke sekolah naik bus maka saya sampai sekolah tepat waktu.
Salah satu bentuk ekuivalen pernyataan majemuk tersebut adalah Jika saya tidak sampai sekolah tepat waktu maka saya pergi ke sekolah tidak naik bus atau. Bentuk ekuivalen pernyataan majemuk yang lainnya untuk pernyataan tersebut adalah Saya pergi kesekolah tidak naik bus atau saya sampai sekolah tepat waktu.
Dalam simbol logika matematika, pernyataan-pernyataan tersebut diberikan seperti daftar berikut.
- p = Saya pergi ke sekolah naik bus.
- q = Saya sampai sekolah tepat waktu.
- Jika saya pergi ke sekolah naik bus maka saya sampai sekolah tepat waktu: p → q
- Jika saya sampai sekolah tidak tepat waktu maka saya pergi ke sekolah tidak naik bus: ~q → ~p
- Saya pergi ke sekolah tidak naik bus atau saya sampai sekolah tepat waktu: ~p ∨ q
Baca Juga: Logika Matematika (Konjungsi, Disjungsi, Implikasi, dan Biimplikasi)
Untuk melihat bentuk ekuivalen pernyataan majemuk tersebut, sobat idschool dapat melihat hasil nilai-nilai kebenaran menggunakan tabel kebenaran. Pembahasan cara membuktikan bentuk ekuivalen pernyataan majemuk akan diulas lebih banyak melalui ulasan di bawah.
Cara Membuktikan Bentuk Ekuivalen Pernyataan Majemuk
Dua pernyataan dikatakan ekuivalen (sama) jika kedua pernyataan majemuk tersebut mempunyai nilai kebenaran yang sama. Sehingga, untuk melihat keabsahan dua bentuk ekuivalen pernyataan majemuk dapat dilihat melalui tabel kebenaran.
Sebagai contoh akan diselidiki tiga pernyataan majemuk yang menjadi contoh sebelumnya yang memiliki dua proposisi tunggal yaitu p = Saya pergi ke sekolah naik bus dan q = Saya sampai sekolah tepat waktu.
Akan diselidiki ekuivalensi dari tiga pernyataan majemuk berikut.
- p → q (Jika saya pergi ke sekolah naik bus maka saya sampai sekolah tepat waktu).
- ~q → ~p (Jika saya sampai sekolah tidak tepat waktu maka saya pergi ke sekolah tidak naik bus saya).
- ~p ∨ q (Saya pergi kesekolah tidak naik bus atau saya sampai sekolah tepat waktu).
Perhatikan tabel kebenaran berikut.
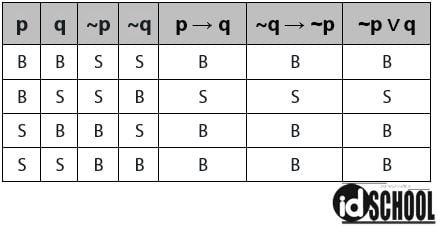
Perhatikan bahwa ketiga kolom p → q, ~q → ~p, dan ~p ∨ q memiliki nilai kebenaran yang sama. Kondisi ini dapat menjadi bukti bahwa ketiga pernyataan majemuk tersebut saling ekuivalen.
Baca Juga: Cara Melengkapi Tabel Kebenaran Logika Matematika
Beberapa hukum proposisi berikut dapat bermanfaat untuk menentukan bentuk ekuivalen pernyataan majemuk:
- Hukum Involusi: ~(~𝑝) ≡ 𝑝
- Hukum De Morgan:
∼ ( 𝑝 ∨ 𝑞) ≡ ∼ 𝑝 ∧ ∼ 𝑞 ∼ ( 𝑝 ∧ 𝑞) ≡ ∼ 𝑝 ∨ ∼ 𝑞
- Hukum Identitas:
𝑝 ∨ 𝑆 ≡ 𝑝
𝑝 ∧ 𝐵 ≡ 𝑝
- Hukum Absorpsi:
𝑝 ∨ ( 𝑝 ∧ 𝑞) ≡ 𝑝
𝑝 ∧ (𝑝 ∨ 𝑞) ≡ 𝑝
- Hukum Null (Dominisasi):
𝑝 ∧ 𝑆 ≡ 𝑆
𝑝 ∨ 𝐵 ≡ 𝐵
- Hukum Komutatif:
𝑝 ∨ 𝑞 ≡ 𝑞 ∨ 𝑝
𝑝 ∧ 𝑞 ≡ 𝑞 ∧ 𝑝
- Hukum Negasi:
𝑝 ∧∼ 𝑝 ≡ 𝑆
𝑝 ∨∼ 𝑝 ≡ 𝐵
- Hukum Asosiatif:
𝑝 ∨ ( 𝑞 ∨ 𝑟) ≡ (𝑝 ∨ 𝑞) ∨ 𝑟
𝑝 ∧ ( 𝑞 ∧ 𝑟) ≡ (𝑝 ∧ 𝑞) ∧ 𝑟
- Hukum Idempoten:
𝑝 ∨ 𝑝 ≡ 𝑝
𝑝 ∧ 𝑝 ≡ 𝑝
- Hukum Distributif:
𝑝 ∨ ( 𝑞 ∧ 𝑟) ≡ ( 𝑝 ∨ 𝑞) ∧ (𝑝 ∨ 𝑟)
𝑝 ∧ ( 𝑞 ∨ 𝑟) ≡ ( 𝑝 ∧ 𝑞) ∨ (𝑝 ∧ 𝑟)
Contoh beberapa bentuk ekuivalen pernyataan majemuk terdapat pada ekspresi-ekspresi logika matematika berikut.
- p → q ≡ ~p ∨ q
- p → q ≡ ~q → ~p
- ~(p → q) ≡ p ∧ ~q
- p → (q → r) ≡ (p ∧ q) → r
- p ↔ q ≡ (p → q) ∧ (q → p)
- p ↔ q ≡ (~p ∨ q) ∧ (~q ∨ p)
- p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
- ~(p ↔ q) ≡ p ↔ ~q
Baca Juga: Negasi Pernyataan Majemuk dengan Konjungsi, Disjungsi, Implikasi, dan Biimplikasi
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara menentukan bentuk ekuivalen pernyataan majemuk. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1: Menentukan Bentuk Ekuivalen Pernyataan Majemuk
Pernyataan yang ekuivalen dengan pernyataan “Jika semua siswa hadir, maka beberapa guru tidak hadir” adalah ….
A. Beberapa siswa tidak hadir atau beberapa guru hadir
B. Semua siswa tidak hadir atau beberapa guru tidak hadir
C. Beberapa siswa tidak hadir atau beberapa guru tidak hadir
D. Beberapa siswa tidak hadir atau semua guru tidak hadir
E. Semua siswa hadir dan beberapa guru hadir
Pembahasan:
Misalkan proposisi dari premis pada soal disimbolkan dalam huruf p dan q seperti berikut.
- p = Semua siswa hadir
- q = Beberapa guru tidak hadir
Negasi dari kedua proposisi tunggal di atas adalah:
- ~p = Beberapa siswa tidak hadir
- ~q = Semua guru hadir
Pernyataan: p → q
Salah satu bentuk pernyataan yang ekuivalen denga p → q adalah ~p ∨ q.
Pernyataan yang sesuai dengan ekspresi logika ~p ∨ q: Jika semua siswa hadir, maka beberapa guru tidak hadir” adalah “Beberapa siswa tidak hadir atau beberapa guru tidak hadir.
Jadi, pernyataan yang ekuivalen dengan pernyataan Jika semua siswa hadir, maka beberapa guru tidak hadir” adalah “Beberapa siswa tidak hadir atau beberapa guru tidak hadir.
Jawaban: C
Contoh 2: Menentukan Pernyataan Majemuk yang Ekuivalen
Pernyataan ~p → q ekuivalen dengan ….
A. p ∧ q
B. p ∨ q
C. ~p ∨ q
D. p ∨ ~q
E. q → p
Pembahasan:
Salah satu cara yang dapat digunakan untuk menentukan bentuk ekuivalen pernyataan majemuk adalah mengasikan dua kali seperti yang dilakukan pada cara berikut.
Mencari pernyataan majemuk yang ekuivalen dengan p → q:
p → q ≡ ~[~(~p → q)]
p → q ≡ ~[~p ∧ ~q]
p → q ≡ ~(~p) ∨ ~(~q)
p → q ≡ p ∨ q
Jadi, pernyataan ~p → q ekuivalen dengan p ∨ q.
Jawaban: B
Contoh 3: Menentukan Pernyataan Majemuk yang Ekuivalen

Pembahasan:
Pernyataan yang senilai adalah bentuk ekuivalen pernyataan. Pernyataan yang diberikan berupa suatu implikasi p → q.
Selidiki masing-masing pernyataan yang diberikan pada soal:
- (1) p → q ≢ q → p, karena merupakan suatu implikasi dan bentuk konvers nya, nilai kebenarannya tidak sama
- (2) p → q ≢ ~p → ~q, karena merupakan suatu implikasi dan bentuk inversnya, nilai kebenarannya tidak sama
- (3) p → q ≡ ~q → ~p, karena merupakan suatu implikasi dan bentuk kontraposisinya
- (4) p → q ≡ ~[~(p → q)] ≡ ~(p ∧ ~q) ≡ ~p ∨ ~(~q) ≡ ~p ∨ q
Jadi, pernyataan yang benar terdapat pada nomor (3) dan (4).
Jawaban: D
Demikianlah ulasan materi bentuk ekuivalen pernyataan majemuk yang dilengkapi dengan bagaimana cara membuktikan kebenarannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Tautologi, Kontradiksi, dan Kontingensi
