Determinan matriks 3×3 dapat dicari melalui dua cara yaitu metode kofaktor dan Aturan Sarrus. Nilai determinan matriks 3×3 berguna untuk mendapatkan solusi dari sistem persamaan linear tiga variabel. Fungsi determinan ini juga berlaku untuk sistem persamaan linear dengan jumlah variabel lainnya (tidak hanya tiga).
Paad matriks 2×2, nilai determinan sama dengan selisih perkalian bilangan antara diagonal utama dengan diagonal sekunder. Diagonal utama adalah bilangan-bilangan pada garis diagonal yang ditarik dari sisi kiri atas ke kanan bawah. Diagonal sekunder adalah bilangan-bilangan pada garis diagonal yang ditarik dari sisi kanan atas ke kiri bawah.

Namun cara mendapatkan determinan matriks 3×3 tidak bisa menggunakan cara seperti itu. Bagaimana cara mendapatkan determinan matriks 3×3 ada di bawah.
Daftar isi:
Baca Juga: Perkalian Matriks 2×2, 3×3, dan mxn dengan nxm
Metode Kofaktor
Ada sebuah teorema untuk menentukan nilai determinan matriks persegi berordo n. Bunyi teoremanya seperti yang diberikan pada pernyataan di bawah.
Teorema: Determinan matriks A yang berukuran n x n dapat dihitung dengan mengalikan entri-entri dalam suatu baris (atau kolom) dengan kofaktor-kofaktornya dan menambahkan hasil-hasil kali yang dihasilkan yakni untuk setiap 1 ≤ i ≤ n dan 1 ≤ j ≤ n,
maka
det(A) = a1jC1j + a2jC2j + … + anjCnj
(ekspansi kofaktor sepanjang kolom ke-j)
Atau
det(A) = ai1Ci1 + ai2Ci2 + … + ainCin
(ekspansi kofaktor sepanjang baris ke-i)
Dari teorema di atas disinggung kofaktor. Apa itu? Definisi kofaktor ada pada pernyataan di bawah.
Definisi:
Jika A adalah matriks kuadrat, maka minor entri aij dinyatakan oleh Mij dan didefinisikan menjadi determinan submatriks yang tetap setelah baris ke-i dan kolom ke-j dicoret dari A. Kofaktor entri aij dinyatakan dalam persamaan Cij = (–1)i+jMij
Teorema dan definisi di atas sekilas sulit untuk dipahami. Namun sebenarnya mudah kok. Simak penjelasan lebih lanjutnya di bawah.
Rumusnya
Minor entri aij dan kofaktor entri aij pada matriks A diperoleh dengan cara berikut.
Coret baris dan kolom pada urutan pertama untuk mendapatkan minor entri a11 dan kofaktor entri a11. Tersisa submatriks yang memilki ukuran 2×2. Minor entri a11 adalah M11 = ei – fh dan kofaktor entri C11 adalah C11 = (–1)2M11 = ei – fh.

Untuk mendapat minor entri a12 dan kofaktor entri a12, coret baris pertama dan kolom kedua. Akan ada submatriks yang memilki ukuran 2×2, sama seperti sebelumnya. Minor entri a12 adalah M12 = di – fg dan kofaktor entri C12 adalah C11 = (–1)3M12 = fg – di.
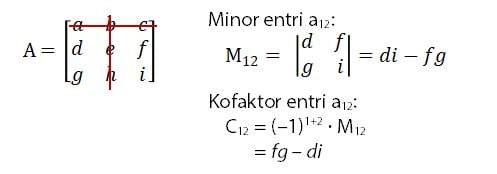
Dengan cara yang sama seperti sebelumnya dapat diperoleh minor entri a13 dan kofaktor entri a13. Minor entri a13 adalah M13 = dh – eg dan kofaktor entri C13 adalah C13 = (–1)4M13 = dh – eg.

Selanjutnya, determinan matriks A dapat dicari menggunakan rumus det(A) = a11C11 + a12C12 + a13C13.
Contohnya
Cara menghitung nilai determinan matriks 3×3 ada pada contoh di bawah.

Baca Juga: Menyelesaikan Sistem Persamaan Linear dengan Matriks
Aturan Sarrus untuk Mencari Determinan Matriks 3×3
Cara yang paling mudah (sejauh ini) untuk menentukan determinan matriks 3×3 adalah menggunakan Aturan Sarrus. Aturan ini merupakan kasus khusus dari metode kofaktor yang terdapat pada matriks berukuran 3 x 3.
Terdapat sebuah matriks A yaitu matriks persegi yang memiliki ukuran 3×3. Ada tiga bilangan disetiap elemen baris dan ada tiga bilangan di setiap elemen kolom.
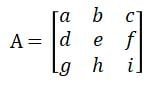
Rumus determinan matriks A pada Aturan Sarrus dalah det(A) aei + bfg + cdh – ceg – afh – bdi.

Cara menggunakan Aturan Sarrus untuk mencari determinan matriks 3×3 ada pada penyelesaian contoh soal di bawah.

Penyelesaian:
det(A) = 4×4×4 + 3×2×3 + 5×1×2 – 5×4×3 – 4×2×2 – 3×1×4
= 64 + 18 + 10 – 60 – 16 – 12
= 4
Diperoleh determinan matriks 3×3 tersebut adalah det(A) = 4. Nilainya sama dengan cara sebelumnya, bukan?
Demikianlah tadi ulasan determinan matriks 3×3 dengan Aturan Sarrys dan metode kofaktor. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Jenis-Jenis Matriks
