Konsep dari operasi hitung untuk perkalian matriks adalah mengalikan elemen-elemen baris pada matriks pertama dengan elemen-elemen kolom pada matriks ke dua. Setiap anggota elemen matriks dikalikan dengan anggota elemen matriks lainnya sesuai urutan dan aturan yang berlaku pada perkalian matriks. Sehingga, perkalian matriks hanya bisa dilakukan untuk banyaknya kolom matriks pertama sama dengan banyaknya baris pada matriks kedua.
Dua buah matriks persegi selalu bisa dilakukan operasi perkalian, misalnya pada matriks dengan ukuran 2 x 2, 3 x 3, dan n x n. Beberapa matriks dengan ukuran tertentu dapat dikalikan dengan mudah. Namun tidak semua matriks dengan kolom dan baris berbeda dapat dikalikan.
Bagaimanakah ciri dua matriks dapat dikalikan? Dan bagaimana pula ciri dua buah matriks tidak dapat dikalikan? Bagaimana cara melakukan perkalian matriks? Sobat idschool dapat mencari tahu jawabannya melalui halaman ini.
Table of Contents
Perkalian Matriks
Sebuah matriks A terdiri dari bilangan-bilangan yang tersusun dalam m baris dan n kolom, ukuran matriks A adalah m x n. Secara umum, penulisan matriks A ditulisan sesuai dengan cara berikut.
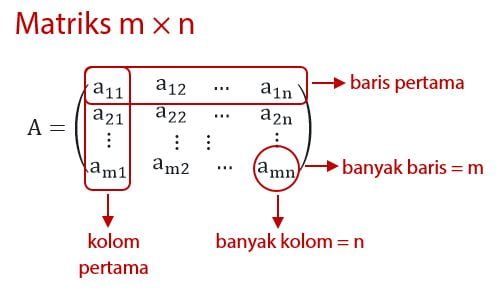
Misalkan diberikan dua buah matriks A dan B. Matriks A memiliki 3 baris dan 2 kolom, dituliskan A3×2. Matriks B memiliki dua baris dan tiga kolom, ditulis dengan B2×3.
Perhatikan bahwa matriks A memiliki 2 kolom dan matriks B memiliki 2 baris. Banyaknya kolom matriks A sama dengan banyaknya baris matriks B. Sehingga, perkalian matriks A dan B dapat dilakukan. Hasil perkalian matriks 3 x 2 dengan matriks 2 x 3 adalah matriks 3 x 3.
Secara umum, ukuran dari hasil perkalian dua matriks dinyatakan pada persamaan di bawah.

Perhatikan perbedaan mana dua buah matriks yang dapat dikalikan dan mana dua buah matriks yang tidak dapat dikalikan berikut.
Contoh dua matriks yang tidak dapat dikalikan
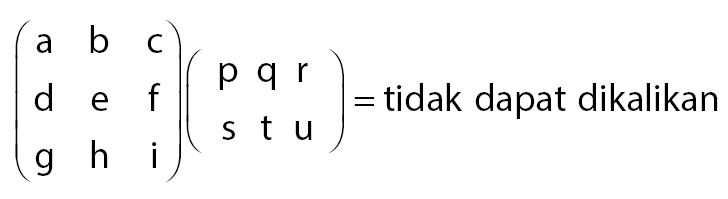
Matriks pertama mempunyai jumlah kolom sebanyak 3 dan matriks ke dua mempunyai jumlah baris sebanyak 2. Karena jumlah kolom pada matriks pertama tidak sama dengan jumlah baris pada kolom ke dua maka dua buah matriks tersebut tidak dapat dikalikan.
Contoh dua matriks yang dapat dikalikan
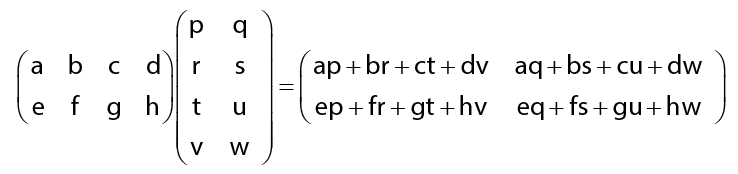
Matriks pertama pada contoh yang diberikan di atas memiliki jumlah kolom sebanyak 4 (empat) dan jumlah baris pada matriks ke dua adalah 4 (empat). Jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks ke dua. Hasil perkalian dua buah matriks ini adalah matriks dengan ukuran 2 x 2.
Baca Juga: Operasi Hitung Mattriks
Perkalian Matriks 2 x 2
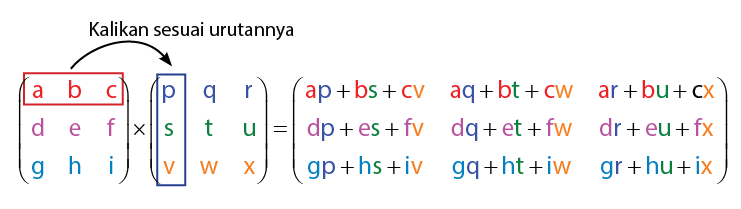
Perkalian dua buah matriks di mana kedua matriks tersebut masing-masing memiliki ukuran 2 x 2 akan menghasilkan matriks dengan ukuran 2 x 2 juga. Proses perkalian matriks ini tidak begitu rumit. Kondisi ini dikarenakan anggota – anggota penyusun matriks dengan ukuran 2 x 2 hanya terdiri atas 4 anggota untuk setiap matriks. Cara mengalikan dua buah matriks adalah mengalikan antar baris dan kolom.
Penjelasan perkalian dua buah matriks dengan ukuran 2 x 2 dalam gambar dapat dilihat seperti berikut.
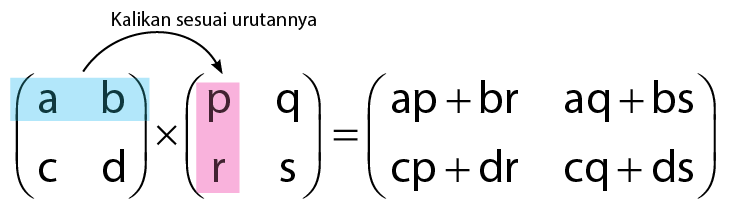
Contoh soal perkalian matriks 2 x 2:
Tentukan hasil perkalian matriks A dan B di bawah!

Jawab:
Operasi hitung untuk perkalian dua matriks tersebut dapat dilakukan seperti cara barikut.
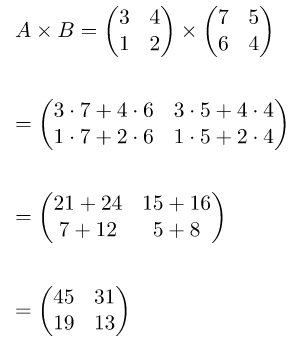
Baca Juga: Determinan dan Invers Matriks
Perkalian Matriks 3 x 3
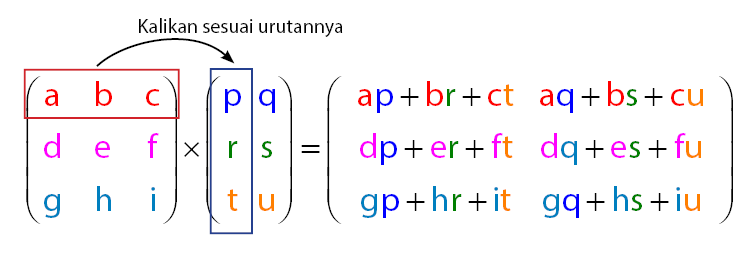
Perkalian dua buah matriks dengan ukuran 3 x 3 sedikit lebih rumit dari perkalian dua buah matriks dengan ukuran 2 x 2. Hal ini dikarenakan ukuran matriks 3 x 3 mempunyai jumlah anggota lebih banyak. Matriks persegi dengan ukuran 3 x 3 memiliki 9 anggota, yang terbagi dalam 3 baris dan 3 kolom. Pada matriks dengan ukuran 3 x 3, setiap baris dan kolom terdiri atas 3 anggota.
Konsep perkalian dua buah matriks dengan ukuran 3 x 3 sama dengan proses perkalian dua buah matriks dengan ukuran 2 x 2, hanya saja lebih rumit. Perhatikan proses perkalian dua buah matriks yang masing-masing berukuran 3 x 3 pada gambar di bawah.
Contoh soal perkalian matriks 3 x 3
Tentukan hasil perkalian matriks 3 x 3 di bawah!

Jawab:
Operasi hitung untuk perkalian dua matriks dengan ukuran 3 x 3 dapat dilakukan seperti cara berikut.

Baca Juga: Pengertian dan Jenis-Jenis Matriks
Perkalian Matriks (m x n) x (n x p)
Ulasan terakhir yang akan dibahas melalui halaman ini adalah perkalian dua matriks dengan ukuran berbeda. Konsep perkalian dua buah matriks masih sama dengan dua pembahasan sebelumnya, yaitu mengalikan antar elemen-elemen matriks pada baris dan kolom.
Sebagai contoh, akan diulas perkalian matriks dengan ukuran 3 x 2 dan matriks dengan ukuran 3 x 2. Perhatikan proses perkalian dua buah matriks yang masing-masing berukuran (3 x 3) x (3 x 2) pada gambar di bawah.
Contoh soal perkalian matriks (3 x 3) x (3 x 2)
Diberikan dua buah matriks A dan B:
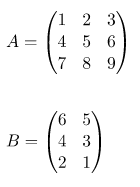
Tentukan hasil perkalian kedua matriks tersebut!
Jawab:
Operasi hitung untuk perkalian kedua matriks tersebut dapat dilakukan seperti cara berikut.
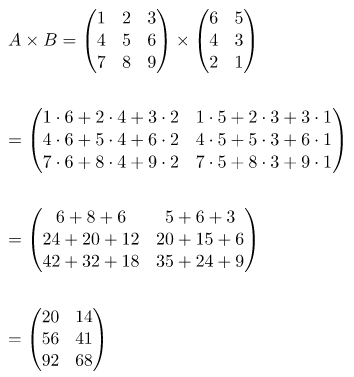
Demikian proses perkalian matriks 3 x 3 dengan 3 x 2, diperoleh matriks dengan ukuran 3 x 2.
Sekian ulasan matriks yang meliputi perkalian matriks 3 x 3, 2 x 2, dan perkalian matriks (m x n) x (n x m). Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear (SPL) dengan Matriks
