Ada dua cara yang dapat digunakan untuk menentukan invers fungsi yaitu cara biasa dan cara cepat. Tentu beberapa dari kalian sangat menyukai cara cepat. Sayangnya, cara menentukan invers fungsi dengan cara cepat hanya berlaku untuk beberapa bentuk soal. Sehingga perlu juga untuk mengetahui bagaimana cara menentukan invers fungsi dengan cara langkah per langkah.
Namun tenang, di tingkat sekolah banyak fungsi f(x) yang memiliki rumus cepat fungsi inversnya. Bagaimana cara menentukan invers fungsi? Bagaimana cara menentukan invers fungsi dengan rumus cepat? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Definisi Fungsi Invers
Invers dari fungsi f(x) adalah f(x)–1, misalnya invers fungsi dari f(x) = 3x adalah f–1(x) = 1/3x. Persamaan fungsi invers tersebut diperoleh dengan cara mengikuti definisi fungsi invers berikut.
Definisi Fungsi Invers:
Jika fungsi f: Df → Rf adalah fungsi bijektif maka invers fungsi f adalah fungsi yang didefinisikan sebagai f–1:Rf → Df dengan Df adalah daerah asal fungsi dan Rf adalah daerah hasil fungsi f.

Secara umum, untuk fungsi f(x) = p memiliki fungsi invers f–1(p) = x dan untuk fungsi f(x) = ax + b memiliki fungsi invers f–1(ax + b) = x.
Ada beberapa langkah yang perlu dilakukan untuk mementukan fungsi invers f(x) = f–1(x). Langkah-langkah untuk menentukan fungsi invers tersebut meliputi beberapa nomor berikut.
- Misalkan f(x) = y
- Variabel y atau f(x) merupakan persamaan yang memuat variabel x
- Ubah persamaan x ke dalam persamaan yang memuat variabel y
- Ubah variabel x menjadi f–1(x) dan variabel y menjadi variabel x
Bagaimana contoh cara mendapatkan fungsi invers fungsi dari suatu fungsi f(x) terdapat pada penyelesaian dua contoh soal berikut.
Soal 1:
Tentukan fungsi invers dari f(x) = 3x – 5!
Fungsi f(x) = 3x – 5 merupakan fungsi linear. Cara menentukan fungsi invers dari fungsi linear dapat dilakukan dengan me seperti cara berikut.
Misalkan y = f(x),
maka: y = 3x – 5
3x = y + 5
x = 1/3(y + 5)
f–1(x) = 1/3(y + 5)
Jadi, fungsi invers dari fungsi f(x) = 3x – 5 adalah f–1(x) = 1/3(y + 5).
Soal 2:
Tentukan fungsi invers f(x) = 1/x+2!
Misalkan f(x) = y sehingga akan menghasilkan persamaan berikut.
*kalikan silang
y(x+2) = 1
xy + 2y = 1
xy = 1 – 2y
Sehingga diperoleh invers fungsi f(x):
Jadi, fungsi invers f(x) = 1/x+2 adalah f–1(x) = 1 – 2x/x.
Baca Juga: Persamaan Matematika yang Merupakan Fungsi
Rumus Cepat Fungsi Invers f(x)
Untuk beberapa fungsi f(x), fungsi inversnya dapat diperoleh dengan rumus cepat. Beberapa bentuk fungsi f(x) dan rumus cepat fungsi inversnya terdapat pada tabel berikut.
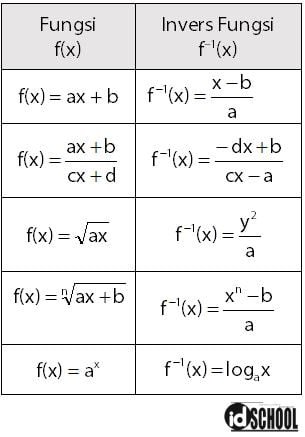
Bagaimana cara menentukan invers fungsi dengan rumus cepat ditunjukkan melalui penyelesaian soal di bawah.
Soal 3:
Tentukan invers fungsi f(x) = 2x+1/3x+5!
Invers fungsi f(x) pada soal dapat dikerjakan dengan rumus pada baris kedua pada tabel yaitu f(x) = ax+b/cx+d → f–1(x) = –dx + b/cx – a.
Fungsi f(x) = 2x+1/3x+5 mempunyai niali a = 2, b = 1, c = 3 dan d = 5. Sehingga cara menentukan invers fungsi f(x) = 2x+1/3x+5 dengan cara cepat menghasilkan persamaan berikut.
Sudah selesai! Diperoleh invers fungsi f(x) = 2x+1/3x+5 adalah f–1(x) = –5x + 1/3x – 2.
Hasil fungsi invers tersebut sama dengan pengerjaan dengan cara runut seperti yang ditunjukkan pada cara berikut.
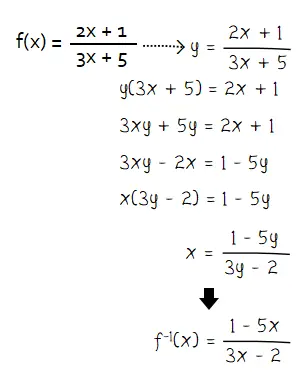
Dengan rumus cepat dan langkah demi langkah menghasilkan fungsi invers untuk f(x) yang sama yaitu f–1(x) = –5x + 1/3x – 2.
Baca Juga: Cara Menentukan Daerah Asal (Domain), Daerah Kawan (Kodomain), dan Daerah Hasil (Range)
Contoh Soal dan Pembahasan
Beberapa contoh soal fungsi invers di bawah dapat sobat idschool gunakan untuk menambah pemahaman materi di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahsan.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih
Contoh 1 – Soal dan Cara Menentukan Invers Fungsi
Diketahui fungsi f dengan rumus f(x) = 2x – 3 dan f–1(x) adalah fungsi invers dari f(x). Nilai dari f–1(3) = ….
A. –2
B. –1
C. 1
D. 2
E. 3
Pembahasan:
Perama perlu untuk mencari fungsi invers dari f(x) = 2x – 3 terlebih dahulu.
Menentukan invers fungsi f(x):
f(x) = 2x – 3
2x = f(x) + 3
x = 1/2(f(x) + 3)
x = 1/2f(x) + 3/2
f–1(x) = 1/2x + 3/2
Diperoleh invers fungsi f(x) = 2x – 3 adalah f–1(x) = 1/2x + 3/2. Selanjutnya substitusi nilai x = 3 pada persamaan f–1(x) untuk mendapatkan nilai f–1(3) seperti yang dilakukan pada penyelesaian berikut.
Menghitung nilai f–1(3):
f–1(3) = 1/2 · 3 + 3/2
f–1(3) = 3/2 + 3/2 = 6/2= 3
Jadi, nilai dari f–1(3) = 2
Jawaban: D
Baca Juga: Sifat-Sifat Komposisi Fungsi (+Contoh Soal dan Pembahasan)
Contoh 2 – Soal dan Cara Menentukan Invers Fungsi
dan f–1(x) adalah invers fungsi f(x). Nilai f–3(3) = ….
A. 4/3
B. 2
C. 5/2
D. 3
E. 7/2
Pembahasan:
Langkah pertama untuk menyelesaikan soal di atas adalah menentukan fungsi invers f(x) yaitu f–1(x) terlebih dahulu. Fungsi invers f(x) pada diperoleh dengan cara cepat berikut.
Rumus cepat fungsi invers:
Fungsi f(x):
Fungsi invers f(x):
Sehingga, fungsi invers untuk f(x) = 1–5x/x+2 adalah:
Substitusi nilai x = 3 pada persamaan f–1(x) untuk mendapatkan nilai f–1(3) seperti yang dilakukan pada cara berikut.
Menghitung f–1(3):
Jadi, nilai f–1(–3) = 7/2
Jawaban: E
Baca Juga: Perbedaan Relasi dan Fungsi
Contoh 3 – Soal dan Cara Menentukan Invers Fungsi
Jika f–1(x) adalah invers fungsi f(x) maka f–1(x – 2) = ….
Pembahasan:
Pertama perlu mencari invers fungsi f(x) terlebih dahulu. Cara menentukan invers fungsi f(x) dapat menggunakan rumus cepat.
Fungsi f(x):
Invers fungsi f(x):
Selanjutnya, substitusi nilai x menjadi x – 2 pada persamaan f–1(x) untuk mendapatkan persamaan f–1(x – 2) seperti yang dilakukan pada cara berikut.
Menentukan persamaan f–1(x–2):
Jadi, jika f–1(x) adalah invers fungsi f(x) maka f–1(x – 2) = 3x–5/x–4, x ≠ 4.
Jawaban: D
Demikianlah tadi ulasan cara menentukan invers fungsi f(x) beserta trik cepat untuk mendapatkan fungsi invers f(x). Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
