Cara menentukan persamaan grafik fungsi kuadrat ada tiga cara. Digunakan untuk tiga bentuk soal berbeda. Cara yang digunakan disesuaikan dengan informasi pada soal. Tiga cara menentukan persamaan grafik fungsi kuadrat dapat menggunakan rumus y = a(x – x1)(x – x2); y = a(x – xp)2 + yp; dan y = ax2 + bx + c.
Rumus y = a(x – x1)(x – x2) digunakan saat diketahui dua titik potong grafik dengan sumbu x. Rumus y = a(x – xp)2 + yp digunakan saat diketahui titik puncak dan satu titik yang dilalui kurva. Sementara rumus y = ax2 + bx + c digunakan saat diktahui tiga titik yang dilalui kurva.
Pembahasan lebih lanjut mengenani cara menentukan persamaan grafik fungsi kuadrat dari gambar ada di bawah.
Daftar isi:
- 1) Cara menentukan grafik fungsi kuadrat saat diketahui 2 titik potong dengan sumbu x
- 2) Diketahui koordinat titik puncak grafik fungsi kuadrat
- 3) Diketahui Tiga Titik Sembarang pada Grafik Fungsi Kuadrat
1) Cara menentukan grafik fungsi kuadrat saat diketahui 2 titik potong dengan sumbu x
Titik potong dengan sumbu x terjadi ketika nilai y = 0. Kurva parabola paling banyak memiliki dua titik potong dengan sumbu x. Dapat hanya memiliki satu titik potong atau tidak memiliki titik potong.
Diketahui sebuah grafik fungsi kuadrat memotong sumbu x di titik (x1, 0) dan (x2, 0). Kurva tersebut juga melalui sebuah titik (x3, y3). Rumus untuk menentukan grafik fungsi kuadrat tersebut adalah y = a(x – x1)(x – x2).
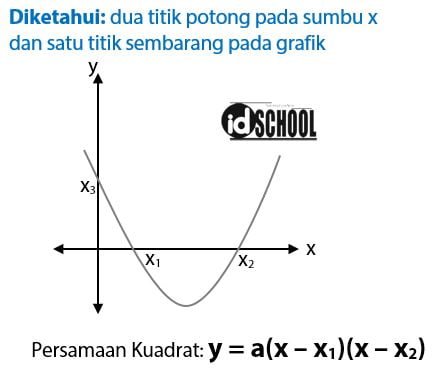
Contoh cara menentukan persamaan grafik fungsi kuadrat jika diketahui titik potong kurva dengan sumbu x dan melalui sebuah titik.
Soal:
Perhatikan gambar di bawah!
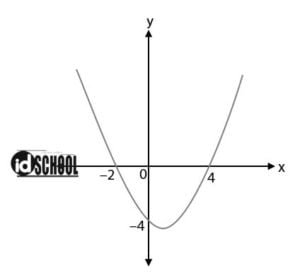
Persamaan grafik fungsi kuadrat pada gambar di atas adalah ….
A. y = x² – ½x – 8
B. y = x² – ½x – 4
C. y = ½x² – x – 4
D. y = ½x² – x – 8
E. y = ½x² – 2x – 8
Jawab:
Diketahui dua titik yang memotong sumbu x adalah (–2, 0) dan (4, 0), serta sebuah titik pada grafik fungsi kuadrat (0, -4).
Rumus yang digunakan: y = a (x – x1)(x – x2)
Mencari nilai a:
–4 = a(0 – (–2))(0 – 4)
–4 = a × 2 × (–4)
Substitusi nilai a ke y = a(x – x1)(x – x2) untuk mendapatkan persamaan y yang dicari seperti berikut.
Jadi, persamaan grafik fungsi kuadrat pada gambar di atas adalah y = ½x² – x – 4.
Jawaban: C
Baca Juga 5 Cara Menggambar Grafik Fungsi Kuadrat
2) Diketahui koordinat titik puncak grafik fungsi kuadrat
Sebuah grafik fungsi kuadrat diketahui letak koordinat titik puncaknya, yaitu (xp, yp). Grafik tersebut diketahui juga melalui (x3, y3). Rumus persamaan grafik fungsi kuadrat tersebut adalah y = a(x – xp) + yp.
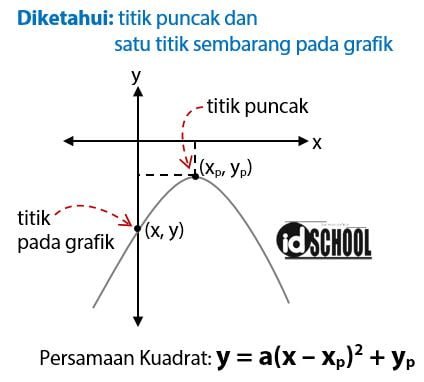
Cara menentukan persamaan grafik fungsi kuadrat yang diketahui memiliki titik potong (xp, yp) dan melalui satu titik terdapat pada penyelesaian soal di bawah.
Soal:
Perhatikan gambar di bawah!
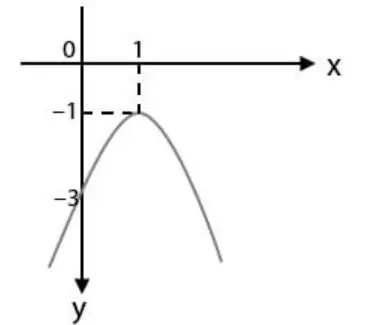
Persamaan grafik fungsi kuadrat pada gambar di atas adalah ….
A. y = –2x2 + 4x – 3
B. y = –2x2 + 4x + 3
C. y = –2x2 – 4x – 3
D. y = 2x2 + 4x – 3
E. y = 2x2 + 4x – 3
Jawab:
Diketahui koordinat titik puncak (1, –1) dan grafik melalui titik (0, –3).
Rumus yang digunakan: y = a(x – xp)2 + yp
Mencari nilai a:
–3 = a(0 – 1)2 + (–1)
–3 = a × 1 – 1
a = –3 + 1
a = –2
Mencari persamaan kuadrat:
y = –2(x – 1)2 + (–1)
= –2(x2 – 2x + 1) –1
= –2x2 + 4x – 3 (A)
Baca Juga: Himpunan Penyelesaian Pertidaksamaan Kuadrat
3) Diketahui Tiga Titik Sembarang pada Grafik Fungsi Kuadrat
Sebuah grafik fungsi kuadrat diketahui melalui tiga titik yaitu A(x1, y1); B(x2, y2); dan C(x3, y3). Kondisi soal seperti ini bisa diselesaikan dengan menggunakan bentuk umum persamaan kuadrat y = ax2 + bx + c.

Cara menentukan persamaan grafik fungsi kuadrat yang diketahui melalui tiga titik ada pada langkah penyelesaian soal di bawah.
Soal:
Perhatikan gambar berikut!

Persamaan dari grafik fungsi di atas adalah ….
A. f(x) = 4/5x2 – x – 4/5
B. f(x) = 3x2 – 4/5x – 4/5
C. f(x) = 4/5x2 – 3x + 4/5
D. f(x) = 4/5x2 + 3x – 4/5
E. f(x) = 4/5x2 – 3x – 4/5
Cara menentukan persamaan grafik fungsi kuadrat:
Substitusi tiga titik pada bentuk umum persamaan kuadrat: f(x) = ax2 + bx + c
Persamaan (1): untuk titik (–1, 3)
3 = a(–1)2 + b(–1) + c
3 = a – b + c
a – b + c = 3
Persamaan 2: untuk titik (1, –3)
–3 = a(1)2 + b(1) + c
–3 = a + b + c
a + b + c = –3
Persamaan 3: untuk titik (4, 0)
0 = a(4)2 + b(4) + c
0 = 16a – 4b+c
16a – 4b + c = 0
Eliminasi a dan c dari persamaan (1) dan (2):

Eliminasi c dari persamaan (1) dan (3):

Selanjutnya subtitusi nilai b = –3 pada persamaan 15a + 5b = –3:
15a + 5(–3) = –3
15a = 12
Substitusi nilai a = 4/5 dan b = –3 ke persamaan (1) untuk mendapatkan nilai c:
4/5 – (–3) + c = 3
4/5 + 3 + c = 3
c = 3 – 3 – 4/5 = –4/5
Diperoleh nilai nilai a = 4/5; b = -3; dan c = –4/5. Maka persamaan grafik fungsi kuadratnya adalah f(x) = 4/5x2 + (–3)x + (–4/5) = 4/5x2 – 3x – 4/5.
Jawaban: E
Demikianlah bahsan cara menentukan persamaan grafik fungsi kuadrat dari gambar. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

maaf , buat ini bagaimana ya titik simetri fungsi kuadrat y=2x Kuadrat 2+4x+3? terima kasih
Halo Heru, kamu dapat menggunakan rumus koordinbat titik puncak nya yaa (xp, yp). Untuk persamana kuadrat y = 2x^2 + 4x + 3 memiliki nilai a = 2, b = 4, dan c = 3.
Sehingga dapat dicari xp:
xp = -b/2a
= -4/2*2
= -4/4
= -1
Sementara yp dapat diperoleh dengan substitusi nilai xp ke persamaan y:
yp = 2xp^2 + 4x + 3
yp = 2(-1)^2 + 4(-1) + 3
yp = 2*1 + 4 *(-1) + 3
yp = 2 – 4 + 3 = 1.
Jadi, dipeorleh titik simetri fungsi kuadrat y = 2x^2 + 4x + 3 adalah (-1, 1). Semoga bermanfaat!
Tq.. so usefull🕊
#majuterus #semngtterus
Tolong di revisi kembali
Halo Ibnu, benar ada sedikit koreksi pada penggunaan tanda +/-, terimakasih komentar dan evaluasinya, salam sukses selalu…