Grafik Fungsi Trigonometri y = sin x, y = 2 sin x, dan y = sin 2x

Cara menggambar grafik fungsi trigonometri dapat dilakukan melalui beberapa langkah. Bentuk grafik fungsi trigonometri berupa grafik periodik yang nilainya selalu berulang berdasar suatu pola. Hal ini sesuai dengan fungsi trigonometri yang termasuk sebagai fungsi periodik. Grafik dari persamaan fungsi trigonometri biasanya akan berulang dengan bentuk yang sama setelah 360^o.

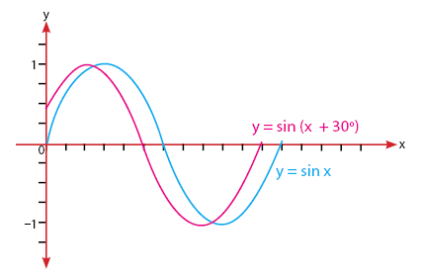
Sinus (sin) merupakan fungsi trigonometri yang menyatakan besar sudut pada segitiga dengan panjang sisi depan dan sisi miring segitiga. Bentuk grafik dari fungsi trigonometri y = sin x seperti dua buah parabola dengan arah buka yang berlawanan dan saling bersambung. Selanjutnya, bentuk grafik dari persamaan y = sin x dapat digunakan untuk mempermudah gambar grafik y = 2 sin x dan y = sin 2x, y = sin (x + 30^o), y = sin x + 1, dan fungsi sinus lainnya.

Baca Juga: Fungsi Trigonometri dan Sudut Istimewa pada Trigonometri

Bagaimana cara menggambar grafik fungsi trigonometri y = sin x? Bagaimana cara menggambar grafik fungsi trigonometri y = 2 sin x, y = sin 2x, atau fungsi yang lain? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Cara Menggambar Grafik Fungsi Trigonometri y = sin x
• Persamaan Umum Grafik Fungsi Sinus Trigonometri

Cara Menggambar Grafik Fungsi Trigonometri y = sin x

Sebelum mulai menggambar grafiknya, persiapkan peralatannya terlebih dahulu. Peralatan yang digunakan untuk menggambar grafik fungsi sinus trigonometri y = sin x adalah kertas, busur, jangka, dan pensil. Oke, mari kita mulai menggambar grafik fungsi trigonometri y = sin x.

Langkah-langkah menggambar grafik fungsi trigonometri y = sin x

1. Buat diagram kartesius, sumbu x mewakili sudutnya (dalam satuan derajat/radian) dan sumbu y mewakili nilai fungsi nya.
2. Buat lingkaran di sebelah kiri sumbu y.
3. Ukur sudut istimewa pada lingkaran menggunakan busur. Tentukan semua letak titik koordinat yang mewakili sudut istimewa dan nilai fungsi trigonometrinya. Sudut istimewa dalam fungsi trigonometri biasanya adalah 30^o, 45^o, 60^o, 90^o, 120^o, 135^o, 150^o, 180^o, 210^o, 225^o, 240^o, 270^o, 300^o, 315^o, 330^o, dan 360^o.
4. Hubungkan titik-titik yang diperoleh.

Cara menggambar grafik fungsi trigonometri fungsi sinus diberikan dalam pembahasan berikut.

Langkah 1:
Buat diagram kartesius, sumbu x mewakili sudutnya (dalam satuan derajat) dan sumbu y mewakili nilai fungsi nya.

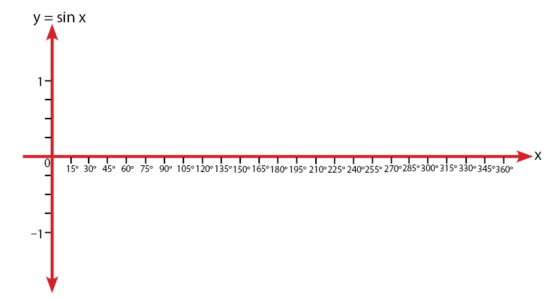
Langkah 2:
Buat lingkaran di sebelah kiri sumbu y.

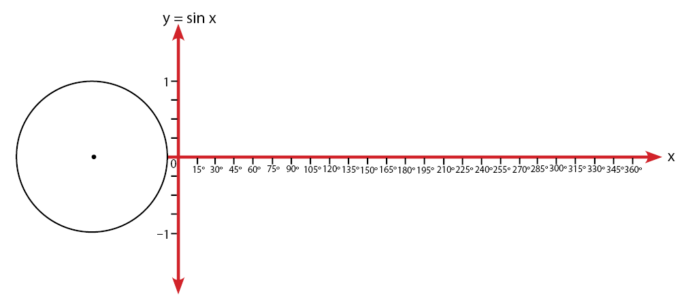
Langkah 3:
Ukur sudut istimewa pada lingkaran menggunakan busur, tentukan semua letak titik koordinat yang mewakili sudut istimewa dan nilai fungsi trigonometrinya.

Sudut 0^o:

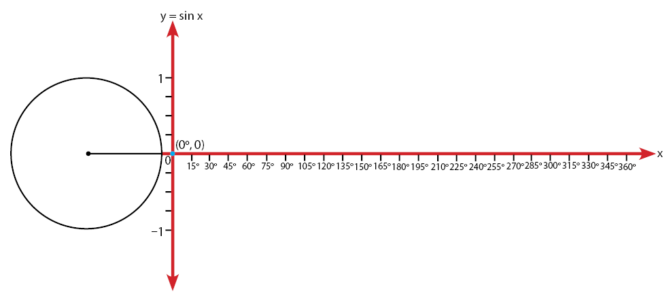
Sudut 30^o:

Sudut 45^o:

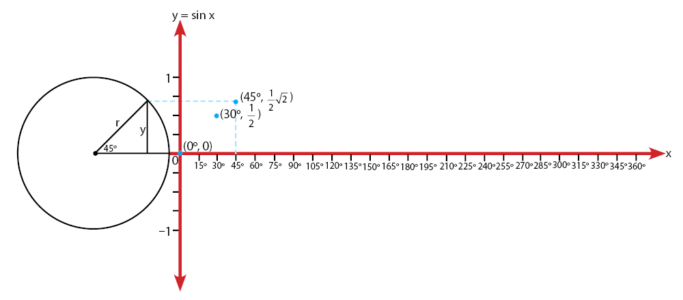
Sudut 60^o:

Sudut 90^o:

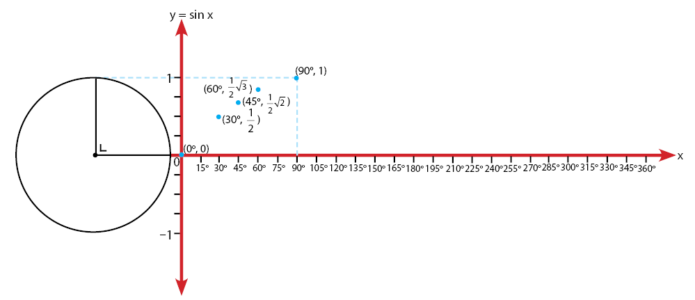
Baca Juga: Cara Menentukan Bayangan Benda Hasil dari Transformasi Geometri

Sudut 270^o:

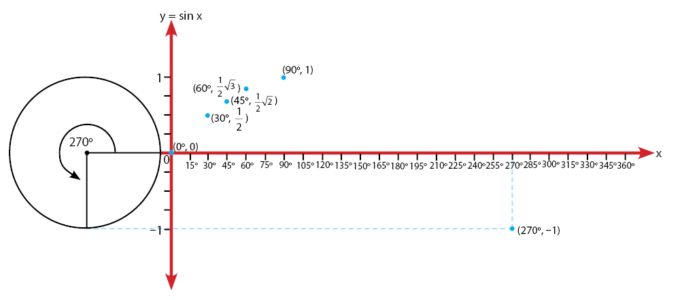
Sudut 300^o:

Lakukan untuk semua sudut istimewa dalam trigonometri sehingga diperoleh hasil seperti berikut.

Langkah 4:
Hubungkan titik-titik yang diperoleh, sehingga terbentuk grafik fungsi y = sin x seperti gambar di bawah.

Baca Juga: Cara Menggambar Grafik Fungsi Trigonometri y = cos x, y = 2 cos x, dan y = cos 2x

Persamaan Umum Grafik Fungsi Sinus Trigonometri

Persamaan umum grafik fungsi sinus trigonometri dapat dinyatakan dalam rumus:

Keterangan:
A = simpangan terjauh/amplitudo
b = banyaknya gelombang dalam rentang satu periode (0 – 2π)
α = pergerakan grafik geser ke kiri (+) atau ke kanan (–)
c = pergerakan grafik geser ke atas (+) atau ke bawah (–)

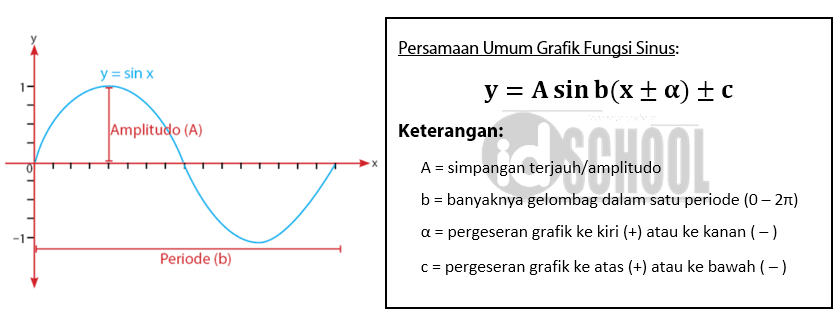
Grafik dasar dari fungsi sinus dan persamaan umum fungsi trigonometri di atas dapat digunakan untuk mempermudah pembuatan grafik sinus lain seperti y =2 sin x, y = sin 2x, y = sin (x + 30), y = sin x + 1, dan lain sebagainya.

Selanjutnya, perhatikan beberapa grafik yang diperoleh dari pengembangan grafik fungsi umum sinus y = sin x dan grafik dasarnya.

Grafik y = sin x dan y = 2 sin x: Nilai Amplitudonya berubah dari 1 menjadi 2.

Grafik y = sin x dan y = sin 2x: Banyaknya gelombang dalam rentang 0 – 2π dari satu gelombang menjadi dua gelombang.

Grafik y = sin x dan y = sin (x + 30): Geser grafik y = sin x ke arah kiri sejauh 30.

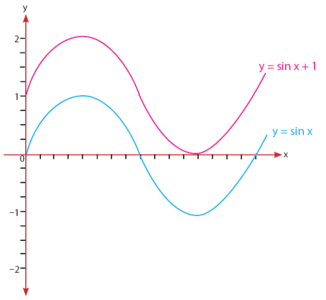
Grafik y = sin x dan y = sin x + 1: Geser grafik y = sin x ke arah atas sebanyak satu satuan.

Sekian pembahasan mengenai Cara Menggambar Grafik Fungsi Trigonometri y = sin x, y = 2 sin x, dan y = sin 2x. Meliputi juga grafik y = sin (x + 30^o) dan y = sin x + 1. Jika ada bagian yang belum paham atau (secara tidak sengaja) ada bagian yang salah bisa dituliskan pada kolom komentar.

Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Cara Menggambar Grafik Fungsi Trigonometri y = cos x, y = 2 cos x, dan y = cos 2x