Fungsi Trigonometri dan Sudut Istimewa pada Fungsi Trigonometri

Trigonometri adalah cabang ilmu matematika yang mempelajari sudut dalam segitiga. Fungsi trigonometri terdiri atas fungsi sinus (sin), cosinus (cos), tangen (tan), dan fungsi kebalikan dari ketiga fungsi tersebut. Cara menentukan nilai fungsi trigonometri dengan sudut istimewa dapat dilakukan tanpa menggunakan alat bantu hitung seperti kalkulator. Namun untuk sudut segitiga yang tidak termasuk dalam sudut istimewa biasanya dibutuhkan alat bantu hitung. Sedangkan untuk membantu sobat idschool dalam mempelajari materi, sobat idschool dapat mencari les matematika terdekat di Jakarta.

Pengertian sudut sendiri adalah suatu bangun yang dibentuk oleh suatu titik pangkal tertentu dan dua sinar dengan titik pangkal yang sama. Tempat titik pangkal yang merupakan pertemuan dua sinar disebut titik sudut. Sedangkan dua sinar tersebut dinamakan kaki sudut. Letak sudut ditunjukkan seperti pada gambar berikut.

Baca Juga: Rumus Luas Segitiga Sembarang dan Cara Menghitungnya

Bagaimana fungsi trigonometri dan bagaimana cara menentukan nilai dari fungsi trigonometri sudut istimewa? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Fungsi Trigonometri
• Sudut Istimewa pada Trigonometri

Fungsi Trigonometri

Fungsi trigonometri meliputi fungsi sinus, cosinus, tangen, dan juga fungsi kebalikan dari ketiga fungsi tersebut. Definisi dari ketiga fungsi berhubungan dengan besar sudut dan panjang sisi segitiga.

Dalam sebuah segitiga siku-siku terdapat tiga buah sisi yang terdiri dari sisi depan, samping, dan miring. Jika sebuah sudut α adalah salah satu sudut pada segitiga tersebut dan panjang ketiga sisi segitiga diketahui maka persamaan fungsi trigonometri dapat ditentukan.

Persamaan fungsi trigonometri pada suatu segitiga dengan besar sudut α sesuai dengan rumus berikut.

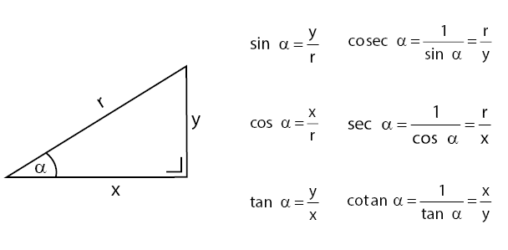
Cara untuk mengingat fungsi trigonometri dapat dilakukan dengan Jembatan Keledai: SinDeMi CosSaMi TanDeSa. Di mana, kepanjangannya adalah Sinus Depan Miring, Cosinus Samping MIring, dan Tangen Depan Samping. Perhatikan sebuah gambar segitiga siku-siku dan keterangan ketiga sisi segitiga berikut!

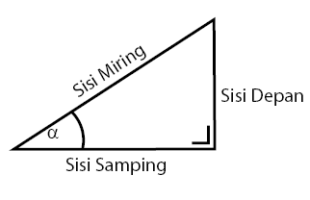
Persamaan fungsi trigonometri berdasarkan gambar segitiga di atas memenuhi persamaan di bawah.

• SinDeMi: Sinus Depan Miring
  sin α = ^{Sisi Depan}/_{Sisi Miring}

• CosSaMi: Cosinus Samping Miring
  cos α = ^{Sisi Samping}/_{Sisi Miring}

• TanDeSa: Tangen Depan Samping
  tan α = ^{Sisi Depan}/_{Sisi Samping}

Baca Juga: Rumus Jumlah dan Selisih Fungsi Sinus & Cosinus

Sudut Istimewa pada Trigonometri

Sebelum membahas mengenai sudut istimewa pada trigonometri dan nilainya, perhatikan dulu pembagian daerah diagram kartesius. Pembagian diagram kartesius dalam empat kuadran dapat mempermudah sobat untuk menentukan nilai fungsi trigonometri.

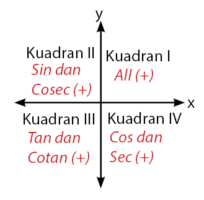
Pada kuadran I semua nilai (sin, cos, tan, dan kebalikannya) bernilai positif. Fungsi trigonometri pada kuadran II yang bernilai positif hanya sin dan kebalikannya (cosec).

Pada kuadran III, fungsi trigonometri yang bernilai postif hanya tan dan kebalikannya (cotan). Sedangkan pada kuadran IV, fungsi trigonometri yang bernilai positif hanya cos dan sec.

Ada beberapa sudut istimewa pada trigonometri yang terdiri dari 0^o, 30^o, 45^o, 60^o, 90^o, dan beberapa sudut istimewa lainnya. Namun sobat idschool hanya perlu mengetahui nilai fungsi sinus untuk sudut istimewa untuk besar sudut 0^o, 30^o, 45^o, 60^o, dan 90^o.

Di mana nilai fungsi sinus dan cosinus untuk 4 sudut istimewa sesuai dengan nilai-nilai berikut.

Nilai sudut istimewa lainnya akan mengikuti sesuai rumus pada fungsi identitas trigonometri yang akan diberikan di bawah.

1. Sudut 90^o ‒ α:
   sin (90^o ‒ α) = cos α
   cos (90^o ‒ α) = sin α

2. Sudut (90^o + α):
   sin (90^o + α) = cos α
   cos (90^o + α) = –sin α

3. Sudut 180^o – α:
   sin (180^o – α) = sin α
   cos (180^o – α) = –cos α

4. Sudut 180^o + α:
   sin (180^o + α) = –sin α
   cos (180^o + α) = –cos α

5. Sudut 270^o – α:
   sin (270^o – α) = –cos α
   cos (270^o – α) = –sin α

6. Sudut 270^o + α:
   sin (270^o + α) = –cos α
   cos (270^o + α) = sin α

7. Sudut 360^o – α:
   sin (360^o – α) = –sin α
   cos (360^o – α) = cos α

8. Sudut α + k × 360^o:
   sin (α + k × 360^o) = sin α
   cos (α + k × 360^o) = cos α

Contoh:
Cari tahu nilai dari sin 300^o!

Jawab:
Pilih salah satu rumus fungsi identitas trigonometri! Misalkan pilih cos (360^o – α) = cos α

Selanjutnya nilai sin 300 dapat dihitung seperti cara berikut.
cos 300^o = cos ( 360^o – 60^o)
cos 300^o = cos 60^o = ¹/₂

Sudut 300^o berada pada kuadran IV, fungsi cosinus pada kuadran IV adalah positif. Dari hasil perhitungan diperoleh nilai cos 300^o = ¹/₂.

Lengkapnya, berikut ini adalah tabel nilai fungsi trigonometri untuk sudut-sudut istimewa dalam derajat pada satu periode.

Sedangkan nilai fungsi trigonometri untuk sudut-sudut istimewa dalam radian pada satu periode sesuai dengan tabel berikut.

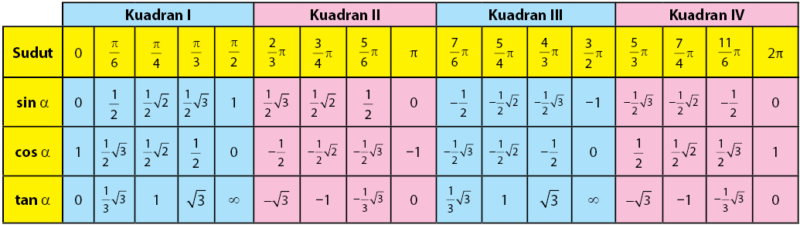
TRIK: menghafal nilai sudut istimewa pada fungsi Sinus dan Cosinus dapat menggunakan grafik fungsi y = sin x dan y = cos x.

Nilai fungsi trigonometri yang perlu hafal bisa hanya untuk fungsi sinus dan cosinus, sedangkan fungsi tangen dapat menggunakan identitas trigonometri. Untuk memperoleh nilai dari fungsi tangen (tan) dari sudut istimewa dapat menggunakan rumus seperti pada persamaan berikut.

Sebagain contoh, diketahui sin 45^o = ¹/₂√2 dan cos 45^o = ¹/₂√2 nilai tan 45^o dapat dihitung seperti cara berikut.

Diperoleh nilai tan 45^o = 1, cara di atas dapat digunakan untuk besar sudut istimewa lainnya,

Demikian pembahasan fungsi trigonometri dan cara menentukan nilai dari sudut istimewa pada fungsi trigonometri. Di era digital ini, sobat idschool dapat lebih mudah untuk belajar melalui berbagai sumber seperti blog edukasi atau platform pendidikan lainnya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Aturan Cosinus