Cara menentukan garis singgung lingkaran yang melalui satu titik dari lingkaran dengan persamaan x2 + y2 + Ax + By + C = 0 dibedakan menjadi dua. Pertama adalah cara menentukan garis singgung lingkaran yang melalui suatu titik pada lingkaran. Kedua adalah cara menentukan garis singgung yang melalui satu titik di luar lingkaran.
Untuk garis singgung yang melalui satu titik pada lingkaran ditentukan dengan rumus garis singgung. Ada tiga rumus garis singgung yang dapat digunakan. Ketiga rumus tersebut digunakan berdasarakan persamaan lingkaran yang diketahui.
Sementara cara untuk menentukan garis singgung yang diketahui melalui satu titik di luar lingkaran ada dua cara. Cara pertama dilakukan menggunakan nilai diskriminan. Dan cara kedua dilakukan dengan persamaan garis kutub (polar).
Bagaimana cara menentukan persamaan garis singgung lingkaran yang diketahui melalui satu titik pada lingkaran? Bagaimana cara menentukan persamaan garis lurus yang melalui satu titik di luar lingkaran dan menyinggung lingkaran tersebut? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah,
Daftar isi:
Baca Juga: Persamaan Lingkaran (Rumus Pusat dan Jari-jari Lingkaran)
Garis Singgung Lingkaran
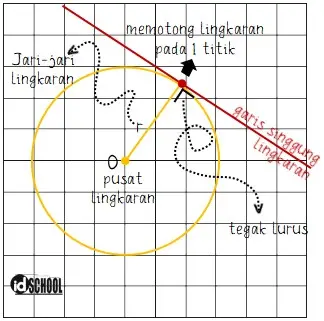
Garis singgung lingkaran adalah garis lurus yang memotong lingkaran tepat pada satu titik. Koordinat titik porong antara garis singgung dengan satu titik pada lingkaran disebut titik singgung.
Garis singgung lingkaran akan selalu tergak lurus dengan jari-jari lingkaran. Contoh bentuk garis singgung linkaran ditunjukkan pada garis lurus berwarna merah pada gambar di bawah.
Baca Juga: Cara Mencari Persamaan Lingkaran yang Diketahui Melalui 3 Titik
Garis Singgung Lingkaran yang Melalui Satu Titik PADA Lingkaran
Kedudukan sebuah titik pada lingkaran dari gambar dapat diketahui dengan melihat letak titiknya. Setiap titik yang terletak tepat pada busur lingkaran berarti kedudukan titik berada pada lingkaran.
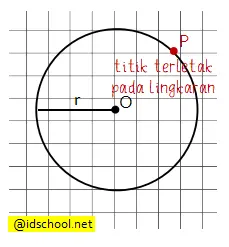
Untuk lingkaran yang diberikan dalam sebuah persamaan, kedudukan titik terhadap lingkaran dapat diketahui dengan cara substitusi nilai koordinat titiknya pada persamaan lingkaran. Titik yang terletak pada lingkaran akan menghasilkan nilai sama dengan jari-jarinya.
Sebagai contoh titik Q(5, 1) pada lingkaran L ≡ (x ‒ 2)2 + (y + 3)2 = 25. Kedudukan titik Q terhadap lingkaran dapat dicari tahu dengan cara substitusi nilai absis (x = 5) dan ordinat (y = 1) pada persamaan L seperti berikut.
Mengetahui kedudukan titik Q:
(x ‒ 2)2 + (y + 3)2
= (5 ‒ 2)2 + (1 + 3)2
= 32 + 42
= 9 + 16
= 25
Hasil substitusi titik (5, 1) pada persamaan lingkaran menghasilkan persamaan (x ‒ 2)2 + (y + 3)2 = 25. Sehingga dapat disimpulkan bahwa titik Q(5, 1) terletak pada lingkaran.
Bentuk umum persamaan garis lurus yang merupakan persamaan garis singgung lingkaran yang melalui satu titik pada lingkaran sesuai dengan tiga persamaan berikut.
| Pers. lingkaran: x2 + y2 = r2 |
| Titik yang dilalui: (x1, y1) |
| Persamaan garis singgung: x1·x + y1·y = r2 |
| Pers. lingkaran: (x‒a)2 + (y‒b)2 = r2 |
| Titik yang dilalui: (x1, y1) |
| Persamaan garis singgung: (x‒a)(x1‒a) + (y‒b)(y1‒b) = r2 |
| Pers. lingkaran: x2 + y2 + Ax + By + C = 0 |
| Titik yang dilalui: (x1, y1) |
| Persamaan garis singgung: x1·x + y1·y + ½A(x+x1) + ½B(y+y1) + C = 0 |
Sebagai contoh, titik Q(5, 1) terletak pada lingkaran (x ‒ 2)2 + (y + 3)2 = 25.
Persamaan garis singgung linkaran yang melalui titik Q(5, 1) dicari tahu dengan cara berikut.
Menentukan persamaan garis singgung:
(x ‒ 2)(5‒2) + (y + 3)(1+3) = 25
3(x ‒ 2) + 4(y + 3) = 25
3x ‒ 6 + 4y + 12 = 25
3x + 4y ‒ 19 = 0
Jadi, persamaan garis singgung lingkaran yang melalui satu titik pada lingkaran adalah 3x + 4y ‒ 19 = 25.
Baca Juga: 3 Kedudukan Garis terhadap Lingkaran
Garis Singgung Lingkaran yang Melalui Satu Titik Di Luar Lingkaran
Sebuah titik dikatakan berada di luar lingkaran jika kedudukan titik berada di luar area luas lingkaran. Substitusi nilai titik di luar lingkaran pada persamaan lingkaran akan menghasilkan nilai yang lebih dari jari-jarinya.
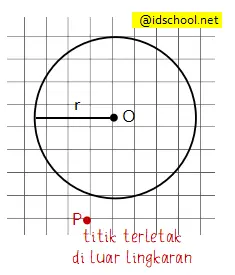
Sebagai contoh kedudukan titik R(7, 1) terhadap lingkaran x2 + y2 = 25. Kedudukan titik R terhadap lingkaran dapat dicari tahu dengan cara substitusi nilai absis (x = 7) dan ordinat (y = 1) pada persamaan L seperti berikut.
Mengetahui kedudukan titik R(7, 1):
x2 + y2
= 72 + 12
= 49 + 1
= 50
Hasil substitusi titik R(7, 1) pada persamaan lingkaran menghasilkan persamaan x2 + y2 = 50 > 25. Sehingga dapat disimpulkan bahwa titik R(7, 1) terletak di luar lingkaran.
Garis singgung lingkaran yang melalui satu titik di luar lingkaran dapat dicari dengan dua cara. Cara pertama dengan memisalkan nilai diskriminan (D = 0). Dan cara kedua adalah dengan garis kutub (garis polar).
Langkah-langkan mencari persamaan garis singgung lingkaran yang melalui satu titik di luar lingkaran dengan nilai diskriminan.
- Misalkan Persamaan Garis Singgung (PGS) lingkaran y ‒ y1 = m(x ‒ x1)
- Substitusi PGS yang diperoleh ke persamaan lingkaran
- Membentuk persamaan nilai disrikiman D = 0
- Melakukan operasi hitung untuk mendapatkan nilai m
- Substitusi nilai m pada pemisalan PGS
Langkah-langkan mencari persamaan garis singgung lingkaran yang melalui satu titik di luar lingkaran dengan garis kutub.
- Membentuk persamaan garis kutub: x1·x + y1·y = r2
- Subsitusi garis kutub ke persamaan lingkaran
- Lakukan operas hitung untuk mendapatkan nilai x
- Subsitusi nilai x dan/atau y yang diperoleh ke persamaan garis kutub untuk menentukan koordinat titik B dan C
- Menentukan persamaan garis lurus singgung lingkaran yang melalui satu titik
Sebagai contoh, akan dicari tahu persamaan garis singgung lingkaran yang melalui satu titik di luar lingkaran dengan nilai diskriman (D) dan garis kutub pada soal berikut.
Soal:
Tentukan persamaan garis singgung lingkaran yang melalui satu titik R(7, 1) pada lingkaran x2 + y2 = 25.
Penyelesaian:
Cara pertama, menentukan persamaan garis singgung lingkaran yang melalui satu di luar lingkaran dengan nilai diskriminan.
1) Misalkan PGS: y ‒ y1 = m(x ‒ x1)
y ‒ 1 = m(x ‒ 7)
y = mx ‒ 7m + 1
2) Substitusi y = mx ‒ 7m + 1 pada persamaan lingkaran x2 + y2 = 25:
x2 + (mx‒7m+1)2 = 25
x2 + m2x2 + (2m‒14m2)x + 49m2 ‒ 14m ‒ 24 = 0
(1+m2)x2 + (2m‒14m2)x + 49m2 ‒ 14m ‒ 24 = 0
3) Membentuk persamaan D = 0:
(2m‒14m2)2 ‒ 4(1+m2)(49m2 ‒ 14m ‒ 24) = 0
4m2 ‒ 28m3 ‒ 28m3 + 196m4 ‒ 4(49m4‒14m3+25m2‒14m‒24) = 0
4m2 ‒ 56m3 + 196m4 ‒ 196m4 + 56m3 ‒ 100m2 + 56m + 96 = 0
‒96m2 + 56m + 96 = 0
12m2 ‒ 7m ‒ 12 = 0
4) Menentukan nilai m:
12m2 ‒ 7m ‒ 12 = 0
12m2 ‒ 16m + 9m ‒ 12 = 0
4m(3m ‒ 4) + 3(3m ‒ 4) = 0
(4m + 3)(3m ‒ 4) = 0
Diperoleh dua nilai m yaitu m = ‒3/4 atau m = 4/3
5) Substitusi nilai m pada pemisalan PGS, sehingga didapat dua persamaan garis singgung lingkaran yang melalui satu titik di luar lingkaran seperti berikut.
Persamaan (i):
y = ‒3/4x ‒ 7(‒3/4) + 1
y = ‒3/4x + 21/4 + 1
4y = ‒3x + 21 + 4
3x + 4y ‒ 25 = 0
Persamaan (ii):
y = 4/3x ‒ 7(4/3) + 1
3y = 4x ‒ 28 + 3
4x ‒ 3y ‒ 25 = 0
Cara kedua, menentukan persamaan garis singgung lingkaran yang melalui satu titik di luar lingkaran menggunakan garis kutub (garis polar).
1) Membentuk persamaan garis kutub: x1·x + y1·y = r2
7x + y = 25
y = 25 ‒ 7x
2) Subsitusi garis kutub ke persamaan lingkaran
x2 + (25 ‒ 7x)2 = 25
x2 + 625 ‒ 350x + 49x2 = 25
50x2 ‒ 350x + 600 = 0
3) Lakukan operas hitung untuk mendapatkan nilai x
50x2 ‒ 350x + 600 = 0
x2 ‒ 7x + 12 = 0
(x ‒ 4)(x ‒ 3) = 0
Diperoleh dua nilai x yaitu x = 4 atau x = 3.
4) Subsitusi nilai x dan/atau y yang diperoleh ke persamaan garis kutub untuk menentukan koordinat titik B dan C
Untuk x = 4:
y = 25 ‒ 7(4)
y = 25 ‒ 28 = ‒3
Koordinat titik B(4, ‒3)
Untuk x = 3:
y = 25 ‒ 7(3)
y = 25 ‒ 21 = 4
Koordinat titik C(3, 4)
5) Menentukan persamaan garis lurus singgung lingkaran yang melalui satu titik
Persamaan (i): garis lurus yang melalui titik B(4, ‒3) dan R(7, 1)
4(x ‒ 4) = 3(y + 3)
4x ‒ 16 = 3y + 9
4x ‒ 3y ‒ 25 = 0
Persamaan (ii): garis lurus yang melalui titik C(3, 4) dan R(7, 1)
‒3(x ‒ 3) = 4(y ‒ 4)
‒3x + 9 = 4y ‒ 16
3x + 4y ‒ 25 = 0
Cara dengan nilai diskriminan dan garis kutub menghasilkan hasil akhir yang sama. Di mana diperoleh dua persamaan garis singgung yang melalui satu titik di luar lingkaran yaitu 4x ‒ 3y ‒ 25 = 0 dan 3x + 4y ‒ 25 = 0.
Baca Juga: Kedudukan Garis terhadap Lingkaran
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idshcool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Garis Singgung Lingkaran yang Melalui Satu Titik
Salah satu persamaan garis singgung melalui titik (a, ‒1) pada lingkaran L ≡ (x + 3)2 + (y ‒ 2)2 = 25 adalah ….
A. 4x + 3y ‒ 31 = 0
B. 4x + 3y + 31 = 0
C. 4x + 3y ‒ 7 = 0
D. 3x + 4y + 31 = 0
E. 3x ‒ 4y ‒ 7 = 0
Pembahasan:
Dari soal diketahui bahwa titik terletak pada lingkaran, sehingga nilai a dapat dicari tahu dengan subsitusi titik (a, ‒1) pada persamaan lingkaran L.
Mencari nilai a:
(a + 3)2 + (‒1 ‒ 2)2 = 25
(a + 3)2 + (‒3)2 = 25
(a + 3)2 + 9 = 25
(a + 3)2 = 25 ‒ 9 = 16
a + 3 = ±√16 = ±4
Diperoleh dua nilai a, yaitu:
(i) a + 3 = 4
a = 4 ‒ 3
a = 1
(ii) a + 3 = ‒4
a = ‒4 ‒ 3
a = ‒7
Sehingga, titik koordinat yang dilalui garis singgung pada lingkaran adalah (1, ‒1) atau (‒7, ‒1).
Diketahui persamaan lingkaran L ≡ (x + 3)2 + (y ‒ 2)2 = 25. Pusat lingkaran L adalah P(‒3, 2) dan jari-jari lingkaran L adalah r = 5.
Rumus persamaan garis singgung yang digunakan:
(x+3)(x1+3) + (y‒2)(y1‒2) = r2
Persamaan garis singgung untuk a = 1:
(x+3)(1+3) + (y‒2)(‒1‒2) = 52
4(x + 3) ‒ 3(y ‒ 2) = 25
4x + 12 ‒ 3y + 6 = 25
4x ‒ 3y ‒ 7 = 0
Persamaan gris singgung untuk a = ‒7:
(x+3)(‒7+3) + (y‒2)(‒1‒2) = 52
‒4(x + 3) ‒ 3(y ‒ 2) = 25
‒4x ‒ 12 ‒ 3y + 6 = 25
‒4x ‒ 4y ‒ 31 = 0
4x + 4y + 29 = 0
Jadi, salah satu persamaan garis singgung lingkaran yang melalui satu titik (a, ‒1) pada lingkaran L ≡ (x + 3)2 + (y ‒ 2)2 = 25 adalah 4x + 3y + 31 = 0.
Jawaban: B
Contoh 2 – Soal Garis Singgung Lingkaran yang Melalui Satu Titik
Persamaan garis singgung lingkaran x2 + y2 ‒ 6x + 4y ‒ 12 = 0 di titik (7, 1) adalah ….
A. 3x ‒ 4y ‒ 41 = 0
B. 4x + 3y ‒ 55 = 0
C. 4x ‒ 5y ‒ 53 = 0
D. 4x + 3y ‒ 31 = 0
E. 4x ‒ 3y ‒ 40 = 0
Pembahasan:
Pertama, perlu diketahui letak kedudukan titik (7,1) terhadap lingkaran terlebih dahulu.
Cara dengan substitusi nili absis (x = 7) dan ordinat (y = 1) pada persamaan lingkaran:
x2 + y2 ‒ 6x + 4y ‒ 12
= 72 + 12 ‒ 6(7) + 4(1) ‒ 12
= 49 + 1 ‒ 42 + 4 ‒ 12
= 0
Dari hasil perhitungan diperoleh hasil substitusi titik (7, 1) pada persamaan lingkaran sama dengan nol. Sehingga dapat disimpulkan bahwa titik (7, 1) terletak pada lingkaran.
Diketahui persamaan lingkaran:
x2 + y2 ‒ 6x + 4y ‒ 12 = 0
Pusat lingkaran:
P(‒½×(‒6), ‒½×4) = P(3, ‒2)
Jari-jari lingkaran:
r = √(¼×(‒6)2 + ¼×42 + 12)
r = √(¼×36 + ¼×16 + 12)
r = √(9 + 4 + 12)
r = √25
r = 5
Rumus garis singgung yang melalui satu titik pada lingkaran x2 + y2 ‒ 6x + 4y ‒ 12 = 0:
(x‒3)(x1‒3)+(y+2)(y1+2) = 52
Titik yang dilalui garis singgung adalah (7, 1). Sehingga persamaan garis singgung lingkaran ditentukan dengan cara berikut.
Menentukan pers. garis singgung:
(x‒3)(7‒3)+(y+2)(1+2) = 52
4(x‒3) + 3(y+2) = 25
4x ‒ 12 + 3y + 6 = 25
4x + 3y ‒ 31 = 0
Jadi, persamaan garis singgung lingkaran yang melalui satu titik pada lingkaran x2 + y2 ‒ 6x + 4y ‒ 12 = 0 di titik (7, 1) adalah 4x + 3y ‒ 31 = 0.
Jawaban: D
Demikianlah tadi ulasan bagaimana cara menentukan garis singgung lingkaran yang melalui satu titik utnuk pada atau di luar lingkaran. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Irisan Kerucut
