Bilangan Berpangkat Pecahan +Contoh Soalnya

Bilangan berpangkat pecahan memiliki bentuk ekuivalen dengan bentuk akar. Sehingga cara menghitungnya dapat menggunakan bentuk akar tersebut. Penyebut pecahan menjadi akar pangkat, sementara pembilang pecahan menjadi pangkat bilangan. Contohnya adalah 8^⅓ = ∛8, sehingga nilai bilangan 8^⅓ = 2 (karena ∛8 = 2).

Contoh lainnya adalah 16^¼ = ∜16 = 2. Untuk pangkat a^½ sama dengan √a (indeks akar 2 biasanya tidak dituliskan). Secara umum, bentuk akar dari bilangan berpangkat pecahan dinyatakan melalui peramasaan berikut.

Bilangan dengan pangkat pecahan dapat dikenai operasi jumlah, kurang, kali, atau bagi. Cara melakukan operasi hitung bilangan berpangkat pecahan ada di bawah.

Daftar isi

• Sifat-Sifat Bilangan Berpangkat Pecahan
• Cara Menghitungnya
• Contoh Soal dan Pembahasan
  • Contoh 1 – Hasil dari 64^(2/3) + 81^(3/4) – (1/5)^-2 adalah …
  • Contoh 2 – Bentuk sederhana dari 9^(1/4)×27^(3/2)/81^(–3/8) adalah ….
  • Contoh 3 – Hasil dari (a‒¼ ‒ a¼)2 × (a ‒¼ + a ¼)2 adalah ….
  • Contoh 4 – Nilai dari (a^⅔ ‒ b^⅔) ‒ ( 1/c )^‒⅓ adalah ….

Sifat-Sifat Bilangan Berpangkat Pecahan

Nilai dari bilangan yang memiliki pangkat pecahan dapat diketahui melalui bentuk akarnya yaitu b^℀ = ^c√b^a. Namun untuk operasi hitungnya akan lebih mudah dilakukan menggunakan sifat-sifat eksponen.

Beberapa sifat eksponen yang berguna, yaitu:

• Pangkat negatif → a⁻¹ = ¹/_a
• Perkalian → a^m × aⁿ = a^{m + n}
• Pembagian → a^m : aⁿ = a^{m – n}
• Bentuk pangkat → (a^m)ⁿ = a^{m × n}
• Bilangan pecahan berpangkat → (^a/_b)^m = ^am/_b^m

Sifat-sifat eksponen di atas dapat diperluas untuk bilangan berpangkat pecahan seperti berikut.

Baca Juga: Cara Menentukan Satuan Bilangan Berpangkat Banyak

Cara Menghitungnya

Operasi hitung bilangan berpangkat pecahan memiliki langkah penyelesaian yang berbeda-beda. Bergantung bagaimana bentuknya. Namun secara umum dapat menggunakan sifat-sifat eksponen.

Contoh cara menyelesaikan operasi hitung bilangan yang memiliki pangkat pecahat ada di bawah.

Soal 1:
Hasil dari 125^⅔ adalah ….
A. 5
B. 15
C. 25
D. 50

Jawab:
Sifat eksponen untuk menyelesaikan operasi hitung bilangan yang memiliki pangkat pecahan ada di bawah.

125^⅔ = (5³)^⅔

= 5^3×⅔

= 5² = 25 (C)

Soal 2:
Nilai dari 4^½ + 8^⅓ = ….
A. 2
B. 4
C. 6
D 8

Penyelesaian:
Penjumlahan dua bilangan yang memiliki pangkat pecahan dapat dilakukan seperti langkah penyelesaian brikut.

4^½ + 8^⅓ = (2²)^½ + (2³)^⅓

= 2^2×½ + 2^3×⅓

= 2¹ + 2¹ = 2 + 2 = 4  (B)

Baca Juga: Rumus Pola Bilangan 2 Tingkat

Contoh Soal dan Pembahasan

Bentuk soal bilangan berpangkat pecahan beserta penyelesaiannya ada di bawah.

Contoh 1 – Hasil dari 64^(2/3) + 81^(3/4) – (1/5)^-2 adalah …

adalah ….

A. 18

B. 28

C. 68

D. 78

Pembahasan:
Untuk menyelesaikan soal di atas dapat menggunakan sifat eksponen.

Cara menghitungnya:

= 2^6×⅔ + 3^4×¾ ‒ (5^‒1)^‒2

= 2⁴ + 3³ ‒ 5² = 16 + 27 ‒ 25 = 18

Jadi, Hasil dari 64^(2/3) + 81^(3/4) – (1/5)^-2 adalah 18

Jawaban: A

Contoh 2 – Bentuk sederhana dari 9^(1/4)×27^(3/2)/81^(–3/8) adalah ….

adalah ….

A. 36½

B. 35½

C. 33½

D. 32½

Pembahasan:
Gunakan sifat eksponen untuk melakukan operasi hitung seperti langkah penyelesaian berikut.

Bentuk sederhana dari 9^(1/4)×27^(3/2)/81^(–3/8) adalah 3^(13/2).

Jawaban: A

Contoh 3 – Hasil dari (a^‒¼ ‒ a^¼)² × (a ^‒¼ + a ^¼)² adalah ….

A. ¹/_a(a² ‒ √a + 1)

B. ¹/_a(a² ‒ 1)

C. ¹/_a(1 ‒ a²)

D. ¹/_a(a ‒ 1)²

E. ¹/_a(a² ‒ √a)

Pembahasan:
Misalkan p = a^‒¼ ‒ a^¼ dan q = a^‒¼ + a^¼

Maka,
p × q = (a^‒¼)² ‒ (a^¼)²
p × q = a^‒½ ‒ a^½

Selanjutnya, cara melakukan operasi hitungnya dilakukan dengan cara berikut.

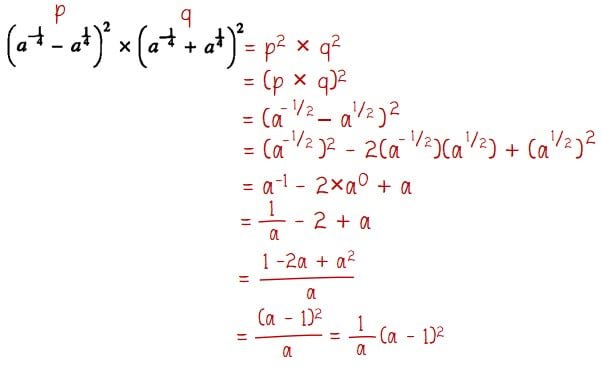
Jadi, hasil dari penyelesaian persamaan yang diberikan pada soal adalah ¹/_a(a ‒ 1)²

Jawaban: D

Contoh 4 – Nilai dari (a^⅔ ‒ b^⅔) ‒ ( ¹/_c )^‒⅓ adalah ….

Diketahui nilai: a = 125, b = 27, dan c = 1.000.

A. 5

B. 6

C. 8

D. 14

E. 15

Pembahasan:
Operasi hitungnya dilakukan dengan cara berikut.

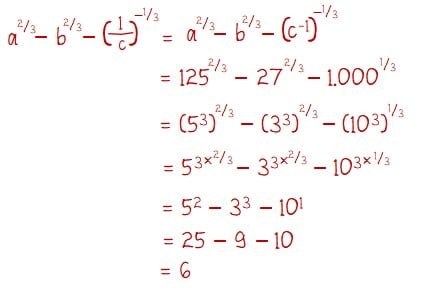
Jadi, nilai dari operasi bilangan tersebut adalah 6.

Jawaban: B

Demikianlah tadi ulasan operasi hitung bilangan berpangkat pecahan beserta contohnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Cara Menjumlahkan Pecahan